Alpha stable distributions

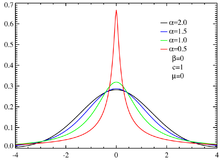
Density functions of some symmetric α-stable distributions

The family of α-stable distributions is a distribution class of continuous probability distributions from stochastics , which are described by the following defining property: are independent, identically distributed random variables , and applies ${\displaystyle X_{1},X_{2},\dotsc ,X_{n},X}$

${\displaystyle X_{1}+X_{2}+\dotsb +X_{n}\sim c_{n}X}$for all and a consequence , ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle (c_{n})_{n\in \mathbb {N} }}$

this is called stable distribution , where “ has the same distribution as ” is to be read. One can show that is the only possible choice . The real number is called the shape parameter. Since the theory of stable distributions was largely shaped by Paul Lévy , these distributions are sometimes called Lévy-stable distributions . ${\displaystyle X}$ ${\displaystyle \sim }$ ${\displaystyle c_{n}=n^{1/\alpha },\alpha \in (0,2]}$ ${\displaystyle \alpha }$

Examples

Although the stable distributions are well-defined for each of the above intervals, the density is only given explicitly for a few special values ​​of α: ${\displaystyle \alpha }$

• The normal distribution with expected value 0 is stable with shape parameters , because it is well known that ${\displaystyle \alpha =2}$

${\displaystyle X_{1},X_{2},\ldots ,X_{n}\sim {\mathcal {N}}(0,\sigma ^{2})\Rightarrow \sum _{i=1}^{n}X_{i}\sim {\mathcal {N}}(0,n\sigma ^{2})\sim n^{1/2}{\mathcal {N}}(0,\sigma ^{2})}$. The normal distribution is the only distribution with the shape parameter . ${\displaystyle \alpha =2}$

• The centered Cauchy distribution satisfies the equation

${\displaystyle X_{1},X_{2},\ldots ,X_{n}\sim {\rm {Cauchy}}(0,a)\Rightarrow \sum _{i=1}^{n}X_{i}\sim n\,{\rm {Cauchy}}(0,a)}$

so it is stable with shape parameters . ${\displaystyle \alpha =1}$

• The (actual) standard Lévy distribution is stable with . ${\displaystyle \alpha ={\frac {1}{2}}}$

properties

α-stable distributions for different values ​​of the skew parameter

• The characteristic function of an α-stable distribution is given by ${\displaystyle \alpha \neq 1}$

${\displaystyle \psi _{\alpha ,\beta }(u)=\exp \left(-|u|^{\alpha }\left(1-i\beta \tan \left({\frac {\pi \alpha }{2}}\right)\operatorname {sgn}(u)\right)\right)}$.

The parameter can be freely selected and is called the skew parameter . ${\displaystyle \beta \in [-1,1]}$

For results ${\displaystyle \alpha =1}$

${\displaystyle \psi _{\alpha ,\beta }(u)=\exp \left(-|u|\left(1+i\beta {\frac {2}{\pi }}\log(|u|)\operatorname {sgn}(u)\right)\right)}$.

• Finite variance only exists for . This follows directly from the central limit theorem . ${\displaystyle \alpha =2}$
• For the distribution has the expected value 0, for there is no expected value. This follows with the law of large numbers . ${\displaystyle 1<\alpha \leq 2}$ ${\displaystyle \alpha \leq 1}$
• All α-stable distributions are infinitely divisible and self-similar (“ self- decomposable”).

literature

• Achim Klenke: Probability Theory. 2nd Edition. Springer-Verlag, Berlin Heidelberg 2008, ISBN 978-3-540-76317-8 , chap. 16.

Individual evidence

1. ^ Rick Durrett : Probability: Theory and Examples. 4th edition. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-76539-8 , p. 141.