Gamma distribution

The gamma distribution is a continuous probability distribution over the set of positive real numbers. It is on the one hand a direct generalization of the exponential distribution and on the other hand a generalization of the Erlang distribution for non-integer parameters. It is used like this

• in queuing theory to describe service times or repair times.
• in actuarial mathematics for modeling small to medium-sized claims .

definition

The gamma distribution is through the probability density ${\displaystyle {\mathcal {G}}(p,\,b)}$ ${\displaystyle f(x)={\begin{cases}{\frac {\displaystyle b^{p}}{\displaystyle \Gamma (p)}}x^{p-1}e^{-bx}&x>0\\0&x\leq 0\end{cases}}}$ Are defined. It has the real parameters and . The parameter is an inverse scale parameter and the parameter is a shape parameter . In order to guarantee that they can be standardized, and is required. ${\displaystyle b}$ ${\displaystyle p}$ ${\displaystyle b}$ ${\displaystyle p}$ ${\displaystyle b>0}$ ${\displaystyle p>0}$ The prefactor is used for correct normalization; the expression stands for the function value of the gamma function , after which the distribution is named. ${\displaystyle b^{p}/\Gamma (p)}$ ${\displaystyle \Gamma (p)}$

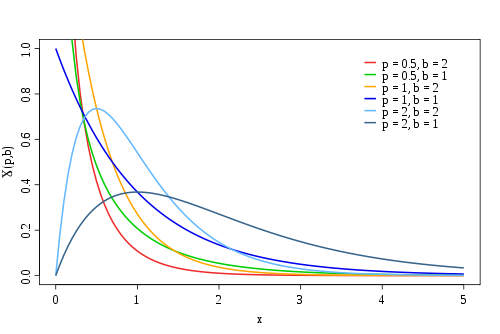
The gamma distribution thus satisfies the distribution function ${\displaystyle F(x)={\begin{cases}P(p,bx)&x\geq 0\\0&x<0,\end{cases}}}$ where is the regularized gamma function of the upper bound. ${\displaystyle P(p,\,bx)}$

Alternative parameterization

As an alternative to the above parameterization, which is common in German-speaking countries, and is also often found ${\displaystyle p}$ ${\displaystyle b}$

${\displaystyle (\alpha =p,\beta =b)}$ or ${\displaystyle \left(k=p,\theta ={\frac {1}{b}}\right).}$

${\displaystyle \beta =b}$is the inversion of a scale parameter and is the scale parameter itself. Density and moments change accordingly with these parameterizations (the expected value here would be, for example, respectively ). Since these parameterizations are predominant in the Anglo-Saxon region, they are used particularly frequently in specialist literature. In order to avoid misunderstandings, it is recommended to state the moments explicitly, for example to speak of a gamma distribution with expected value and variance . The parameterization and the corresponding parameter values ​​can then be clearly reconstructed from this. ${\displaystyle \theta =1/b}$ ${\displaystyle \alpha /\beta }$ ${\displaystyle k\theta }$ ${\displaystyle p/b}$ ${\displaystyle p/b^{2}}$

properties

The density has its maximum for at the point and for at the points ${\displaystyle f}$ ${\displaystyle p>1}$ ${\displaystyle x_{M}={\tfrac {p-1}{b}}}$ ${\displaystyle p>2}$

${\displaystyle x_{W}=x_{M}\pm {\frac {(p-1)^{\frac {1}{2}}}{b}}}$

Turning points.

Expected value

The expected value of the gamma distribution is

${\displaystyle \operatorname {E} (X)={p \over b}.}$

Variance

The variance of the gamma distribution is

${\displaystyle \operatorname {Var} (X)={p \over b^{2}}.}$

Crookedness

The skewness of the distribution is given by

${\displaystyle \operatorname {v} (X)={\frac {2}{\sqrt {p}}}.}$

Reproductivity

The gamma distribution is reproductive : the sum of the stochastically independent gamma distributed random variables and , both of which are gamma distributed with the parameters and or , is in turn gamma distributed with the parameters and . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle b}$ ${\displaystyle p_{x}}$ ${\displaystyle p_{y}}$ ${\displaystyle b}$ ${\displaystyle p_{x}+p_{y}}$

Characteristic function

The characteristic function has the form

${\displaystyle \phi _{X}(s)=\left({\frac {b}{b-is}}\right)^{p}.}$

Moment generating function

The moment generating function of the gamma distribution is

${\displaystyle m_{X}(s)=\left({\frac {b}{b-s}}\right)^{p}.}$

entropy

The entropy of the gamma distribution is

${\displaystyle H(X)=\ln \left(\Gamma (p)\right)-\ln \left(b\right)+(1-p)\psi (p)+p}$

where denotes the digamma function . ${\displaystyle \psi (p)}$

Sum of gamma-distributed random variables

If and are independent gamma-distributed random variables then the sum is also gamma-distributed, namely ${\displaystyle X_{1}\sim {\mathcal {G}}(p_{1},b)}$ ${\displaystyle X_{2}\sim {\mathcal {G}}(p_{2},b)}$ ${\displaystyle X_{1}+X_{2}}$

${\displaystyle X_{1}+X_{2}\sim {\mathcal {G}}(p_{1}+p_{2},b).}$

In general: if stochastically independent then is ${\displaystyle X_{i}\sim {\mathcal {G}}(p_{i},b)\quad i=1,\ldots ,n}$

${\displaystyle X_{1}+\dotsb +X_{n}\sim {\mathcal {G}}(p_{1}+\dotsb +p_{n},b).}$

The gamma distribution thus forms a convolution half-group in one of its two parameters.

Relationship to other distributions

Relationship to beta distribution

If and are independent gamma distributed random variables with parameters and , then the size is beta distributed with parameters and , for short ${\displaystyle X\sim {\mathcal {G}}(p_{1},b)}$ ${\displaystyle Y\sim {\mathcal {G}}(p_{2},b)}$ ${\displaystyle p_{1},b}$ ${\displaystyle p_{2},b}$ ${\displaystyle {\tfrac {X}{X+Y}}}$ ${\displaystyle p_{1}}$ ${\displaystyle p_{2}}$

${\displaystyle \operatorname {Beta} (p_{1},p_{2})\sim {\frac {{\mathcal {G}}(p_{1},b)}{{\mathcal {G}}(p_{1},b)+{\mathcal {G}}(p_{2},b)}}.}$

Relationship to the chi-square distribution

• The chi-square distribution with degrees of freedom is a gamma distribution with the parameters and . ${\displaystyle k}$ ${\displaystyle p=k/2}$ ${\displaystyle b=1/2}$

Relationship to the Erlang distribution

The Erlang distribution with the parameter and degrees of freedom corresponds to a gamma distribution with the parameters and and provides the probability of the time until the occurrence of the -th rare, Poisson-distributed event. ${\displaystyle \lambda }$ ${\displaystyle n}$ ${\displaystyle p=n}$ ${\displaystyle b=\lambda }$ ${\displaystyle p}$

Relationship to the exponential distribution

• If you choose the parameter in the gamma distribution , you get the exponential distribution with parameter . ${\displaystyle p=1}$ ${\displaystyle \lambda =b}$
• The convolution of exponential distributions with the same results in a gamma distribution with . ${\displaystyle n}$ ${\displaystyle \lambda }$ ${\displaystyle p=n,b=\lambda }$

Relationship to the logarithmic gamma distribution

If gamma is distributed, then log gamma is distributed . ${\displaystyle X}$ ${\displaystyle Y=e^{X}}$

literature

• Bernard W. Lindgren: Statistical Theory. Chapman & Hall, New York et al. 1993, ISBN 0-412-04181-2 .
• Marek Fisz : Probability Theory and Mathematical Statistics. 11th edition. Deutscher Verlag der Wissenschaften, Berlin 1989, ISBN 3-326-00079-0 .
• P. Heinz Müller (Hrsg.): Probability calculation and mathematical statistics. 5th, arr. and substantially exp. Edition. Akad.-Verlag, Leipzig 1991, ISBN 3-05-500608-9

Web links

• see also Lévy process , with a picture of a gamma process
• Interactive applet from the University of Konstanz to display the gamma distribution: http://www.uni-konstanz.de/FuF/wiwi/heiler/os/vt-gamma.html
• Calculated evidence: http://www.eisber.net/StatWiki/index.php/WS2_Zettel1#Gamma-Dertteilung