Entropy (information theory)
Entropy (after artificial word ἐντροπία)'s information theory a measure of the average information content of a message. The term is closely related to entropy in thermodynamics and statistical mechanics .
The information-theoretical understanding of the term entropy goes back to Claude E. Shannon and has existed since around 1948. In that year Shannon published his fundamental work A Mathematical Theory of Communication and thus shaped modern information theory.
Entropy is usually denoted with a large eta ( ).
definition
Claude Elwood Shannon defined the entropy of a discrete, memoryless source (discrete random variable) over a finite alphabet consisting of characters as follows: First, each probability of an event is assigned its information content. Then the entropy of a sign is defined as the expected value of the information content
- .
Let , then the probability with which the character of the alphabet occurs is or equivalent
- ,
with . It is set (according to the limit value ). Due to the definition, summands with vanishing probability therefore do not contribute to the sum.
The entropy for words of length is given by
- ,
where is the probability with which the word occurs. The entropy is then the limit of it:
- .
If the individual signs are stochastically independent of each other , then applies to all , i.e. (see block entropy )
interpretation
Entropy is a measure of the mean information content per character of a source that represents a system or an information sequence. In information theory, information is also referred to as a measure of eliminated uncertainty . In general, the more characters that are received from a source, the more information is obtained and, at the same time, the uncertainty about what could have been sent decreases.
The definition of information content can be clearly justified as follows: If an event that can occur with probability actually occurs, then a concrete event is selected from a hypothetical set of equally probable, stochastically independent events . In order to be able to distinguish this number of events, one needs binary bits. This value therefore indicates the information content of a special event in bits. If you weight the actual information content of the possible events with the respective probability of occurrence, you get the mean or expected information content of a sign.
The unit 1 Shannon is defined as the information content of an event with the probability . An example of such an event is a heads result of a coin toss .
Base 2 for the logarithm is arbitrary. It just turns out that bits (binary digits) are particularly easy to handle technically. If another base were chosen, for example 3, one would get ternary digits ( trits ). The information content can easily be converted from bits to trits by multiplying by the modulus .
The minimum necessary number of bits necessary for representation of the information (the text), the average information content of a character is determined by the product and the number of characters in the information text .
Shannon's original intention to use entropy as the measure of the required bandwidth of a transmission channel was quickly generalized. Entropy was generally viewed as a measure of information content. If the entropy is small, the information text contains redundancies or statistical regularities.
The entropy is generally not given by (1). For example, the probability of finding a 0 or 1 in the character string is just as great as in a character string that has arisen from statistically independent events (e.g. repeated coin toss). Therefore, the entropy of individual characters is the same for both strings, although the first string is less random. Already shows a difference: the first string delivers , the second delivers . You can also interpret it this way: The probability of a character depends on the previous character. So there is no stochastic independence.
For successive events that are not stochastically independent, the entropy of successive dependent events is continuously reduced. In such a case, one can also work with the conditional entropy and the source tropy, both of which are based on composite probabilities.
Transinformation , which indicates the strength of the statistical relationship between two random variables, is also closely related to conditional entropy .
In even simpler terms, entropy is the average number of decisions (bits) that are needed to identify or isolate a character from a set of characters.
It makes sense to have an alphabet made up of at least two different characters. An alphabet size of one means that you can neither get new information about newly arriving characters from the transmitter source, nor can you reduce the uncertainty about the previous character.
Maximum entropy value and normalization
If one would like to have a standardized measure for the entropy of any discrete distribution , it is advantageous to use the maximum possible entropy that is achieved with uniform distribution for normalization. Let the number of characters be above the alphabet , then the maximum entropy is given if
- ,
- then is .
From this it follows, for example, for a binary distribution ( ), so one bit per character and character is required for the complete information . This value is reached when zeros and ones appear equally often. If one now normalizes the entropy of any distribution with different symbols , one obtains:
The entropy obtained in this way is always at most equal .
In order to be able to compare the entropies of messages of different lengths, the entropy rate was introduced, which relates the entropy to the individual character (see there).
Examples
alphabet
If distributed evenly, no character can be dispensed with in an alphabet. In contrast, the frequency of letters in the German language is uneven, see also: Entropy (cryptology) . For example, the letter E is seven times as common in German as M or O , which leads to redundancy in the alphabet. Now you want to determine how great this redundancy is.
Be the size of the alphabet. The redundancy R is calculated with . For the German alphabet, an entropy of 4.0629 bits / character is calculated based on the frequency of letters . The maximum entropy is bit / character. This is followed by a redundancy of bits / characters. If you also calculate the total redundancy, which results from the sum of the redundancies of each character, you get bits. Now it would be interesting to know how many characters this corresponds to from our alphabet. If you divide the redundant bits by the average information content of a uniformly distributed character, you get characters → 3 characters (without redundancies). However, if you calculate (⇒ 4 characters), you determine the number of characters with a redundancy that is also present in the alphabet.
The alphabet could be reduced by four letters without any loss of information. This consideration only takes into account the statistical distribution of the letters. Frequent letter combinations such as SCH or ST are ignored ( conditional entropy ) as well as letters that sound the same ( Q , K ).
coin toss
In a coin toss ideally have head or number equally likely. If the entropy is taken as a measure of the uncertainty , it will have a maximum value here. It is completely uncertain whether the next roll head or number is thrown.
Let be a discrete random variable and the expected value with
- (Head) and
- (Number),
Entropy bit results from the above definition .
In other at a jointed coin, such a coin in the middle in 60% of cases head and only in 40% of cases the number indicates. The uncertainty is less here than with the normal coin, as one has a certain preference for heads . Measured as entropy, the uncertainty is only around 0.971.
The sum of the probabilities is always 1.
The entropy can be calculated from the sum of the partial entropies:
If you replace with the expression , you get the formula
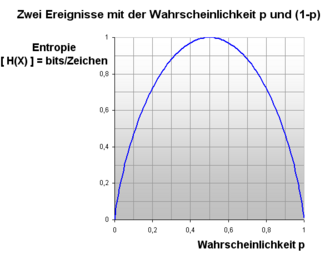
This can be represented graphically as follows:
For each one can read off the entropy directly from it. The function is symmetrical to the straight line . At steep it drops to an entropy value of 0. The entropy also drops to 0 for values that approach the safe event of .
This relationship applies to a random event. In the case of several random events, the individual entropies have to be added up so that entropies over 1 can easily be achieved. The probability, on the other hand, always remains between 0 and 1, by definition, even with repetitions.
If you repeat the coin toss twice, the number of possibilities increases to four. The probability of each individual possibility is 0.25. The entropy of tossing a coin twice is then 2 Sh. If you repeat an ideal coin toss several times, the entropy simply adds up. The entropy of a series of 20 coin tosses ideal calculated simple . This is shown in the picture.
One cannot simply calculate the entropy from a value of the probability. Entropy affects the entire random process. Every partial probability of a possible result is included in the calculation of the entropy of the overall process. Specifying a partial entropy for every possible result makes little sense. In Shannon's entropy formula, the sum of the probabilities should result in 1, otherwise the result can be misleading.
If you save a sequence of coin tosses as a bit sequence, then it makes sense to head always by 0 and number always by one to represent (or vice versa). More compact codings are possible for marked coins , for example the Huffman coding .
Ideal cube
When throwing an ideal dice with six possibilities, the entropy is greater than 1. In general, the entropy is greater than 1 for a random event with stochastically independent random variables from a random experiment with more than two equal possibilities in the result space . With equally probable possibilities in the result space, their value is calculated as follows:
Let n be the number of possibilities, then are the probabilities and the entropy
- .
The ideal cube has six possibilities in the result space. From this follows the entropy for a single throw:
The entropy of a roll of an ideal figure-of-eight cube is easy to calculate: It has eight equal possibilities.
The entropy of a toss with the ideal figure of eight corresponds to the entropy of three tosses with the ideal coin.
The figure shows the relationship between the entropy and the number of equal possibilities of a random experiment.
Entropy tests
Entropy tests are used to test how well data can be compressed or to test random numbers. As a random number test, the entropy of a certain number of random numbers is determined and from a minimum value, for example 7 bits per byte, it is considered passed. However, there are many such tests because the entropy is ambiguous; it can be defined bit-based or byte-based, for example.
A simple example:
A source, such as a dice or a coin, only outputs the values 0xAA (decimal 170) and 0x55 (decimal 85), both with the same probability. The output is 50% 0 or 1 bit-wise, 50% 0xAA or 0x55 byte-wise. The bitwise entropy is (with )
while the byte-wise entropy with
is significantly smaller.
The manufacturer of this random number generator will of course specify the entropy of the device as the bit-wise entropy, i.e. 1. Similarly, a programmer of a compression program will, if possible, choose the basis for which the entropy is minimal (here bytes), i.e. the data can be compressed best.
This example is not very realistic because only two of 256 possible values are used, but if the other bytes are also output with a small probability of, for example, 1/123456789, this does not change the bit-wise entropy and the byte-wise hardly increases; it stays below 1/2. Only when the byte probabilities approach 1/256 does the byte-wise entropy reach the value 1, but then there can still be correlations between the bytes, e.g. the sequence 0xaaaa be much more frequent than the sequence 0x5555 . This is the main reason why there are so many different random number tests.
This ambiguity is not possible with the entropy coating, since there is not only added over probabilities, but also over ergodic probabilities of states, state transition probabilities and conditional probabilities. It is calculated using the theory of the Markov chain . However, the computational effort for real random number generators is high.
It is important to explain that entropy tests only measure equal probability, not true unpredictability. The difference between true random number generators and pseudo random number generators is immeasurable.
Data compression and entropy
The entropy coding is a compression algorithm to compress data without loss. In this context, the cross entropy and the Kullback-Leibler divergence play a role as a measure of the wastage of bits triggered by poor coding.
Example:
- The character string ABBCAADA is given (see also entropy coding ).
- The letters probability: ; ;
- Maximum entropy ( ):
- The maximum entropy can also be calculated with the formula of the maximum entropy:
Alternative ways of quantifying information
Another approach to measuring the information content of a message is given by the Kolmogorow Complexity , in which the shortest possible algorithm for the representation of a given character string indicates the complexity of the message. The logical depth is defined similarly , but it relates to the time complexity of an algorithm for generating the data. Gregory Chaitin also went beyond Shannon's definition of the entropy of information (see Algorithmic Information Theory ).
Similarity to entropy in physics
In physics (see thermodynamics , especially entropy ) an identically named variable plays an essential role. The physical entropy differs from the Shannon information entropy by an additional normalization factor , the Boltzmann constant , and by the replacement of the base used in the logarithm (the dual logarithm is replaced by the natural logarithm ). Thus, physical entropy and mathematical entropy differ in the positive conversion factor , provided with its physical unit. The connection was established through a thought experiment called Maxwell's demon .
See also
- Abnormality (information theory)
- Block entropy
- Differential entropy for continuous distributions
- Entropy (cryptology)
- Entropy estimate
- Source tropy
- Rényi entropy
- Transinformation and Kullback-Leibler Divergence
literature
- CE Shannon: A Mathematical Theory of Communication . In: Bell System Technical Journal . tape 27 , no. 3 , 1948, p. 379-423 , doi : 10.1002 / j.1538-7305.1948.tb01338.x ( PDF ).
- Claude Elwood Shannon and Warren Weaver : The Mathematical Theory of Communication , University of Illinois Press 1963, ISBN 0-252-72548-4 (softcover) and ISBN 0-252-72546-8 (hardcover)
- Rolf Johannesson: Information theory , Addison-Wesley 1992, ISBN 3-89319-465-7
- Norbert Bischof : Structure and Meaning , 1998, ISBN 3-456-83080-7 (The book is written for social scientists and explains mathematical relationships to non-mathematicians in a very understandable way. Chapter 2 is devoted to information theory.)
- Sven P. Thoms: Origin of Life . Fischer, Frankfurt a. M. 2005, ISBN 3-596-16128-2 (The book is written from a biological and chemical perspective. One chapter deals with the relationship between life and entropy.)
- Thomas Cover: Elements of Information Theory , Wiley-Interscience 2006, ISBN 0-471-24195-4 (The book is only available in English. It covers information theory in detail and is mathematical.)
- Martin Werner: Information and Coding , Vieweg 2002, ISBN 3-528-03951-5
Web links
- Introduction of entropy as a total random set with many examples and explanations of Shannon's formula
- Entropy and information
- Owen Maroney: Information Processing and Thermodynamic Entropy. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
- Shannon entropy calculator (text) (English)
- Shannon entropy calculator (binary )
Individual evidence
- ↑ a b Kulturgeschichte der Physik , Károly Simonyi, Urania-Verlag, Leipzig 1990, ISBN 3-332-00254-6 , p. 372.
- ^ CE Shannon: A Mathematical Theory of Communication . In: Bell System Technical Journal . tape 27 , no. 3 , 1948, p. 379-423 , doi : 10.1002 / j.1538-7305.1948.tb01338.x ( PDF ).
- ↑ Concrete similarities between Shannon's information entropy and thermodynamic entropy are shown below. a. treated in: U. Krey, A. Owen, Basic Theoretical Physics - A Concise Overview , Berlin, Springer 2007, ISBN 978-3-540-36804-5 and in: Arieh Ben-Naim: Statistical Thermodynamics Based on Information: A Farewell to Entropy . 2008, ISBN 978-981-270-707-9
- ↑ WA Kreiner: Thermodynamics and Information Theory - Interpretations and differences in meaning in the concept of entropy . doi: 10.18725 / OPARU-4097 A comparative comparison





![{\ displaystyle \ mathrm {H} _ {1} = E [I] = \ sum _ {z \ in Z} p_ {z} I (z) = - \ sum _ {z \ in Z} p_ {z} \ log _ {2} p_ {z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7fbc917ad48fde87cbc498fce378159f1d428fc)