thermodynamics
The thermodynamics (from ancient Greek θερμός Thermos , German , warm ' , as well as ancient Greek δύναμις Dynamis , German , force' ) or thermodynamics is a natural and engineering discipline . It has its origins in the study of steam engines and investigated the question of how heat can be converted into mechanical work . For this purpose, it describes systems made up of a sufficient number of particles and their state transitions using macroscopic state variables, which represent statistical functions of the detailed many-body states. As an engineering science it is important for the various possibilities of energy conversion and in process engineering it describes the properties and behavior of substances that are involved in processes. The French physicist Sadi Carnot , who wrote his pioneering work in 1824, is considered to be the founder .
The main principles of thermodynamics are of great importance and occupy a position similar to that of Newton's axioms in classical mechanics or the Maxwell equations in electrodynamics . The first law states that the total energy in a closed system is constant and is valid as energy conservation in all of physics. The second law expresses the direction in which energy conversions are possible. Thus, it is possible, for example, mechanical, electrical or chemical energy completely in heat energy to convert (thermal energy). Thermal energy, on the other hand, can only be partially converted into these energies and only with great technical effort.
In thermodynamics there are two different approaches that differ in whether substances are viewed as a continuum that can be divided at will, or whether they are viewed as a collection of particles such as atoms or molecules :
- The older approach regards substances as a continuum and is called classical, phenomenological or technical thermodynamics (also technical thermodynamics ) and uses terms such as heat , pressure , volume and temperature . It is part of classical physics and many engineering sciences. If the systems under consideration consist of at least particles, which is always the case with technical systems, this is a very good approximation.
- The statistical thermodynamics contrast, starts from individual particles and describes them because of their large number of statistical methods and the kinetic theory of gases . It is therefore part of statistical physics and explains, for example, how the pressure of a gas on the container is created by collisions between the individual molecules of the gas or how the temperature is related to the kinetic energy of the particles. This approach thus serves as an explanation for various phenomena and as a theoretical foundation for the main clauses, but offers no advantages for analysis or calculation in engineering, so that it is not pursued there.
On the one hand, thermodynamics deals with different processes when heat is involved without going into the specifics of the substances involved. Cycle processes that occur frequently in technology are of particular importance . On the other hand, it makes statements about substances such as the various states of aggregation and their change (melting, boiling, evaporating ...) or chemical reactions that are very dependent on the respective substances.
meaning
Thermodynamics is of great importance in the natural sciences , since energy is involved in all processes occurring in nature. This also includes living beings. In addition, it offers a deeper insight into the properties of matter, which on the one hand is helpful for understanding physical properties or changes in aggregate states and on the other hand is important to understand which chemical reactions can take place and which cannot. Within physics, it is also emphasized that thermodynamics can combine various independently developed subject areas such as classical mechanics or quantum mechanics, which is made possible in particular by the universal concept of energy.
In engineering , thermodynamics is important for the design , calculation and analysis of numerous machines or systems. These include the various heat engines (steam engine, gas or steam turbine, diesel engine), the work machines (pumps, compressors, ...), air conditioning and refrigeration technology , heat and mass transfer , industrial furnaces , supply and disposal technology or energy technology (power plants).
story

The French physicist Nicolas Léonard Sadi Carnot investigated the amount of heat in a steam engine (1824). He found that hot water vapor heats a colder water reservoir and does mechanical work in the process. Carnot suspected that no heat was lost in this process. Carnot described the processes in the steam engine as a cycle, which Émile Clapeyron presented in mathematical form in later years ( Carnot cycle ).
The German doctor Julius Robert Mayer formulated (1841) the thesis that energy should be a constant quantity in a closed system. Energy cannot disappear, it can only be converted into another form. This realization is known as the law of conservation of energy . Mayer made calculations for converting heat into mechanical energy. He stated how much energy corresponds to the temperature increase of 1 g of water by 1 ° C and calculated that this amount of energy corresponds to mechanical energy that could lift 1 g of matter 367 meters (in fact, it is 426 meters). These calculations formed the basis of the first law of thermodynamics. James Prescott Joule determined the mechanical heat equivalent more precisely in 1844.
In 1840 the Swiss - Russian chemist Hermann Heinrich Hess published a paper entitled Thermochemical Investigations, which was based on the theorem of the conservation of energy in molecules or atoms due to the heat of chemical reaction.
While Carnot still suspected that the amount of heat in a steam engine was completely retained, Mayer assumed that forms of energy could be converted into one another. The German physicist Rudolf Clausius linked the ideas of Mayer and Carnot in 1854. He showed that when a steam engine is operated, heat always flows from a warmer reservoir into a colder reservoir and that Carnot's basic thesis is therefore correct. However, the heat energy does not remain constant - as Carnot assumed - it is partly converted into mechanical work. Clausius found that the thermal energy of a machine (steam engine) can only be partially converted into mechanical work; the other part of the energy is released into the environment. The efficiency of a machine indicates the conversion ratio of the mechanical energy gained to the heat supplied. Clausius' insight forms the second law of thermodynamics: “There is no periodically functioning machine that does nothing other than convert heat into mechanical work.” The amount of heat that cannot be used for mechanical work is given off to the environment. Clausius combined this unusable amount of heat with the corresponding temperature to create a new function, entropy . All natural energy conversion processes contain an irreversible entropy component, in which unused heat is given off to the environment. Entropy means an "inward-looking, i. H. Energy that can no longer be transformed or used. ”Later, Boltzmann understood, quite clearly, the entropy as a measure of the disorder of the movements of a system. Only in a closed system and with a reversible change of state does the entropy difference between the initial and final state remain equal to zero.
The French chemist Marcelin Berthelot assumed the heat that developed in the process as the driving force for a chemical reaction (1862).
Hermann Helmholtz linked the electrical energy in batteries with chemical energy and thermal energy. In his treatise on the conservation of force, he developed the law of conservation of energy independently of Mayer.
In later years Helmholtz dealt with energetic questions in chemical reactions. Helmholtz agreed with Berthelot that heat is released during many chemical transformations; however, there were also transformations that produced cold. In his treatise The Thermodynamics of Chemical Processes, Helmholtz divided the energy into free and bound energy during the transformation of substances. Helmholtz combined the internal energy and the free energy with the product of entropy and temperature. According to Helmholtz, material conversions are only possible when the free energy decreases. The American physical chemist Josiah Willard Gibbs , almost simultaneously between 1875 and 1878, came to similar considerations as Helmholtz. The relationship between the enthalpy difference minus the product of the entropy difference and temperature is called the difference in free enthalpy . The relationship is called the Gibbs-Helmholtz equation in honor of the two scientists . With this equation, the chemist can make statements about the material conversion of molecules and calculate the necessary temperatures and concentrations of chemical conversions.
In addition to classical thermodynamics, the kinetic gas theory was developed. According to this, gases consist of particles, atoms or molecules that move freely in empty space between relatively rare collisions. When the temperature rises, the particles move faster and exert greater pressure on the vessel walls through more frequent and violent impacts. Important representatives of this theory were August Krönig , Rudolf Clausius, James Clerk Maxwell and Ludwig Boltzmann . Maxwell and Boltzmann used probability theory to describe thermodynamic quantities on a molecular basis.
In 1999, the physicists Elliott Lieb and Jakob Yngvason presented an axiomatic system in which the definition of entropy is based on the concept of adiabatic accessibility and is based on a strictly mathematical basis in the form of 15 axioms . The temperature is only a variable derived from entropy as a basic variable. The concept of adiabatic accessibility is based on an axiomatic justification by Constantin Carathéodory from 1909. Since this theory has no effect on the results, it has so far not been used in practice - and in teaching only as an exception.
Due to the relatively long history of thermodynamics and the broad areas of application, the descriptions in technical thermodynamics (e.g. when describing an internal combustion engine or a refrigerator), chemical thermodynamics (e.g. when describing a chemical reaction) and the statistical thermodynamics (e.g. when describing ordered quantum states in solids) often have significantly different formalisms.
chronology
The following chronological sequence shows essential theoretical knowledge and the resulting technical developments:
- 1st century AD : Heron of Alexandria builds the first heat engine, the rotating Heronsball , and an opener for temple doors (machine no. 37).
- 1613 : The thermometer is invented, but when exactly and by whom is not clear. Galileo Galilei ascribes this invention to himself and in 1613 his student Gianfrancesco Sagredo confirmed to him that he was able to use Galileo's thermometer successfully.
- 1669 : Richard Towneley recognized the relationship between pressure and volume at constant temperature when measuring barometric altitude. Although Robert Boyle made the law known as Townley's hypothesis , today it is only known as Boyle-Mariott's law , since it was independently discovered by Edme Mariotte and published in 1676.
- 1690 : Denis Papin describes the principle of a first, simple steam engine . Five years later he built a steam pressure pump and Thomas Savery developed a piston-free pump using Papin's ideas.
- 1708/09 : Daniel Gabriel Fahrenheit developed an accurate thermometer, the specialty was the calibration over three points. He set the zero point on his temperature scale, depending on the source, as the lowest temperature he recorded that winter in Gdansk or a mixture of ice-salt and cold. He set the freezing point of water at 32 ° F, the third point was 180 ° F higher and was 212 ° F. Some sources suspect that 180 was chosen because it is a highly composite number and therefore allows a particularly large number of equal divisions on the scale, but this has not yet been proven.
- 1712 : Thomas Newcomen delivers his first steam engine to a mine in Staffordshire.
- 1760 : Joseph Black determines the heat of fusion of ice and the heat of vaporization of water. Black's most famous student was probably James Watt .
- 1787 : Antoine Laurent de Lavoisier publishes the theory of heat substance ( caloricum ), according to which heat is a substance that is absorbed or given off by other substances. The previous doctrine of the phlogiston , which was valid up to that point , nevertheless held up for a long time.
- 1798 : Benjamin Thompson (Earl of Rumford) provided with attempts at cannon drilling the proof that the thermal substance theory of Lavoisier (Caloricum) and also of Phlogiston could not be correct, but his work and conclusions were not heeded for a long time.
- 1811 : Amedeo Avogadro postulated that under the same conditions (pressure, temperature, volume) there is always the same number of particles in a volume. The Avogadro constant (particles per mole ) is named after him. It took until 1865 before Josef Loschmidt was able to present concrete figures for the Avogadro constant for the first time.
- 1816 : The clergyman Robert Stirling applies for a patent for his hot air machine.
- 1822 : Joseph Fourier publishes his book Analytical Theory of Heat , in which he explains heat conduction and develops the transformation named after him to describe the behavior over time .
- 1824 : Sadi Carnot publishes a paper in which he describes the conditions and limits of heat conversion by a periodically working machine.
- 1827 : The Scottish botanist Robert Brown discovers the shaky movement of very small pollen in water.
- 1833 : Joseph Louis Gay-Lussac recognized the dependence of pressure and volume on temperature. Here, too, an ideal gas is implicitly assumed.
- 1842 : Julius Robert Mayer postulates that heat is a form of energy. In 1847 Hermann von Helmholtz, who had not known Mayer's work, formulated this again and more precisely.
- 1852 : The Joule-Thomson effect is discovered by William Thomson (Lord Kelvin) and James Joule. It describes the change in temperature of gases when the pressure changes.
- 1856 : William Thompson describes the change in heat conduction when an electric current also flows in the conductor ( Thompson effect )
- 1857 : Rudolf Clausius explains the gas pressure from the mean kinetic energy of the gas molecules. It is still based solely on their translational movement.
- 1858 : Étienne Lenoir builds the first gas engine that works in the two-stroke process without compression.
- 1859 : The Kirchhoff radiation law by Gustav Robert Kirchhoff describes the connection between absorption and emission of radiation from a body when it is in thermal equilibrium.
- 1860 : James Clerk Maxwell gives the function for the velocity distribution of the particles.
-
1865 : Rudolf Clausius introduces the concept of entropy after he has established that, in addition to the first law (conservation of energy), another axiom is required for the description of thermodynamics.
Josef Loschmidt determines the number of particles per volume, which his student Ludwig Boltzmann then calls the Loschmidt constant . - 1867 : Nikolaus Otto and Eugen Langen present their gas engine at the World Exhibition in Paris in 1867 and received a gold medal for it. The energy consumption could be reduced to 1 ⁄ 3 compared to Lenoir's motor , which some jurors seemed so implausible that they looked for hidden gas lines.
- 1871 : Carl von Linde describes a new refrigeration process in an article. The first pilot project comes about with a brewery and forms the cornerstone of Linde AG .
- 1873 : Johannes Diderik van der Waals publishes his equation for an improved description of gases, which includes the ideal gas equation as a special case.
- 1876 : Josiah Willard Gibbs publishes the phase rule named after him , which explains substances and mixtures with several phases in thermodynamic equilibrium.
- 1877 : Ludwig Boltzmann interprets entropy statistically. In doing so, he discovers the universal Boltzmann constant named after him .
- 1882 : The first commercial steam power plants, built by Thomas Alva Edison's companies, go on stream at Pearl Street Station (New York) and Holborn Viaduct (London). To this day, steam power processes dominate the conversion of energy in thermal power plants.
- 1883 : Hermann von Helmholtz introduces the concept of free energy , which, however, unrelated to the free energy of the pseudoscience has to do, but a thermodynamic potential is
- 1891 : Carl von Linde develops the Linde process named after him for the liquefaction and separation of air.
- 1892 : Rudolf Diesel registers his patent for an internal combustion engine. Since the equal printing process is not yet described in this patent , but a later patent is based on the priority of this patent, patent disputes arise.
- 1893 : James Dewar invents an insulating vessel named after him for his experiments in low-temperature physics , which is also used in ordinary thermos flasks.
- 1897 : Rudolf Diesel's first test engine is running at the Augsburg machine works. In terms of consumption, the test engine is clearly superior to engines of other types, so that it will be brought into series production despite major technical challenges.
- 1900 : Max Planck explains the radiation of the ideal black body ( Planck's law of radiation ) and thus resolves the phenomenon of the ultraviolet catastrophe . At the same time, he lays the foundation for quantum theory , since his model only provides for discrete energy packets (energy quanta) and determines Planck's quantum of action .
- 1905 : Albert Einstein explains Brownian molecular motion in his work "On the motion of particles suspended in liquids at rest, required by the molecular kinetic theory of heat" . He only writes about Brownian molecular movement that the literature is too imprecise for him to identify it with the phenomenon he has explained, but in 1906 another contribution appears, “On the theory of Brownian movement” .
- 1906 : Walther Nernst sets up the 3rd law (heat theorem).
- 1944 : Erwin Schrödinger brings up the term negentropy in order to resolve the apparent contradiction of the organizing and constructive abilities of life and the second law.
- 1953 : Zoran Rant introduces the term exergy to characterize the available work that can be obtained from thermal energy. About ten years later he also developed the term anergy .
- 1974 : Stephen Hawking develops a theory according to which black holes also give off heat radiation and thus follow the 2nd law.
- 1977 : Ilya Prigogine receives the Nobel Prize in Chemistry for his work on non-equilibrium thermodynamics .
Important terms in thermodynamics
Thermodynamics relates the process variables heat and work at the system boundary with the state variables that describe the state of the system.
On the basis of four fundamental principles as well as material-specific, empirical equations of state between the state variables (see e.g. gas law ), thermodynamics allows statements to be made about which changes are possible in a system (e.g. which chemical reactions or phase transitions can take place by setting up equilibrium conditions) , but not how) and which values of the intensive state variables are required for this. It is used to calculate the heat energy released, changes in pressure, temperature or volume, and is therefore of great importance for the understanding and planning of processes in chemical plants, in heat engines as well as in heating and air conditioning technology .
In order to describe systems and properties briefly and precisely, certain terms and agreements are used again and again in thermodynamics:
- The thermodynamics is primarily concerned with the entropy and thermal energy (heat energy) that are included in each system. In an insulated system, the temperature is a measure of the thermal energy it contains.
- In thermodynamics, energy is understood as the sum of two parts, namely exergy and anergy , where each part can be 0. The exergy can be converted into other forms of energy (technical work), i.e. work or be converted into anergy. Technical work is always pure exergy and therefore entropy-free. Anergy can no longer be converted into other forms of energy.
- The environment or the state of the environment serves as a reference for the ability of a system to perform work. Systems that are not in thermodynamic equilibrium with the environment still have exergy, while the energy of the environment is pure anergy.
- A state variable describes a property of the system . Extensive state variables such as internal energy U , entropy S , volume V and number of particles N change when the system is divided. Intensive state variables such as temperature T , pressure p , concentration n and chemical potential μ remain the same.
- A system changes from one state to another through a process . A process variable is, for example, an added heat flow or a dissipated power.
- If a state variable remains the same during a state change (process), it is identified with the prefix iso . Are usual isochoric (receives the volume, as in the constant-volume process ), isobaric (maintains the pressure, as in the constant-pressure process ), isothermal (obtains the temperature), isenthalp (receives the enthalpy) or isentropic (hence receives the entropy, reversible); An isentropic change of state takes place adiabatically and without friction. Isentropic is not to be confused with isotropic !
- Closed or isolated systems do not exchange materials or energy with their environment, closed systems can at least exchange energy and both material and energy flows go through open systems .
- Adiabatic processes and containers are heat-tight, but can exchange materials and work. Work density or rigid systems do not exchange work with the environment (except push work in stationary flow processes ) and diathermic systems only transfer heat to the outside.
- System boundaries or balance envelopes are virtual boundaries for analyzing a system ( material flow analysis ). The change in a state variable within the system boundary can be considered in a balance equation
- A reversible process can be reversed at any time without changing the environment. Reversible processes form the theoretical boundary between possible / real and non-natural processes. Reversible processes are isentropic and are both adiabatic and frictionless.
- An ideal gas is a simplified model for highly dilute gases in which the individual particles have practically no cohesive effect on one another and in which the intrinsic volume of the gas atoms or molecules is negligible.
- If a real gas has the inversion temperature , it maintains its temperature during a throttling process . Below the inversion temperature, it cools down due to the throttling, above it it heats up. Ideal gases get their temperature when throttled.
- Circular processes run cyclically and always bring their working materials back to their original state. Left-hand cycle processes consume work ( refrigeration machines , heat pumps ), right-hand cycle processes deliver work ( heat engines ).
- The Carnot process is an ideal cycle. Since heat can never be completely converted into technical work (exergy), the efficiency of the Carnot process indicates the maximum amount of work that can be obtained from heat.
- Solid, liquid and gaseous phases of a substance can only exist at the same time at the triple point . Since the triple point has a fixed pressure and temperature, triple points are suitable as reference points for calibrating a temperature scale. The triple point of water (0.01 ° C) is used for the Kelvin scale.
- At the critical point , the molecules of a substance are as tightly packed in the gas as they are in the liquid. The critical point is determined by temperature, pressure and density. Above its critical temperature, a gas can no longer be liquefied by pressure.
- A fluid can be a gas or a liquid. In particular, when the change (phase transition) of a substance between liquid and gaseous is considered, the term fluid simplifies the description, as it is not limited to a phase.
In thermodynamic formulas, certain letters are used again and again for certain quantities. Capital letters in formulas denote an absolute quantity , for example V as volume [m³]. Lower case letters designate specific quantities , for example v as volume flow (volume related to a mass, [m³ / kg]), a mass flow [kg / s] or an amount of substance [m³ / mol].
- The thermodynamic or absolute temperature T is measured in Kelvin (up to 1954: degrees Kelvin). 0 Kelvin (−273.15 ° C) cannot be achieved with thermodynamic means (3rd law).
- The internal energy U is the energy stored as heat in the system, the enthalpy H also contains the energy stored in pressure × volume.
- The entropy S is a measure of the disorder and at the same time a measure of the probability of a state. Entropy can never decrease in a closed system . Systems always strive for the state of the highest possible entropy of their own accord (2nd law).
- Volume change work w = ∫ p · dv is done when the volume changes against the prevailing pressures. On the one hand, this is the pressure of the compressed fluid and the pressure of the environment.
- The amount of substance N is a measure of the number of particles and is measured in the unit mol .
- The heat capacity describes the ability of a substance to absorb heat energy. The greater the heat capacity, the smaller the temperature change when absorbing or releasing heat.
Brief summary of the main clauses
- Zero law of thermodynamics: Introduction of temperature as a basic physical quantity: If two systems are in thermodynamic equilibrium with a third , they are also in equilibrium with one another. The variable of state that is the same in these systems is the temperature.
- First law of thermodynamics : The energy of a closed system is constant.
- Second law of thermodynamics : Thermal energy cannot be converted into other types of energy to any degree.
- Third law of thermodynamics (Nernst theorem): The absolute zero point of temperature is inaccessible.
Zero main clause

If a system A is in thermal equilibrium with a system B and B is in thermal equilibrium with a system C , A is also in thermal equilibrium with C. The state variable that is the same in these systems is the temperature , which is scalar , intense and the same everywhere in the system.
In other words: if the equilibrium is transitive , then two systems in contact have the same temperature if and only if they are in thermal equilibrium, i. H. when heat is no longer exchanged between them.
Example: A thermometer is itself a system and should be designated as B. If B indicates the same temperature for a system A as for a system C, it can be concluded that A and C will also be in thermal equilibrium with one another if they are brought into contact. This main clause was formulated after the other three main clauses. But since it forms a foundation of thermodynamics, it was later referred to as the "zeroth" law .
However, it should be noted in the gravitational field that the equilibrium lies between systems A, B and C at generally different temperatures, because the photons of the black body radiation experience a red or blue shift in the gravitational field due to the equivalence principle ; due to the time dilation , they are emitted at different heights at different rates. In addition, their trajectories are curved, so that not all photons starting from below can also arrive at the top. All of these effects cause the temperature to decrease with altitude. On earth this effect is only 1.6 · 10 −14 K / m and is therefore immeasurably small. In the case of a neutron star , however, it is not negligible.
First law
The 1st law of thermodynamics describes the conservation of energy in thermodynamic systems. It says that the energy of a closed system is constant. Based on this statement, energy balances for closed and open systems can be created.
Balance for the closed thermodynamic system
Every system has an internal energy (= extensive state variable ). This can only change through the transport of energy in the form of work and / or heat across the boundary of the system, i.e.:
Here, the infinitesimal change of the work done on the system working (more precisely, the sum of the volume of work and the system dissipated work ., For example, the frictional work), featuring inexact differentials , while complete differentials features. Equivalent extensive working terms can be used in place of volume work. For example, for a magnetic system in a magnetic field, when the magnetic moment of the sample is increased, extensive work is done.
The equation applies to the system at rest. In the case of a moving system, the external energies (potential and kinetic energy) are added:
The energy of a closed system remains unchanged. Different forms of energy can transform into each other, but energy can neither be generated from nothing nor can it be destroyed. Therefore a perpetual motion machine of the first kind is impossible (no system does work without supplying another form of energy and / or without reducing its internal energy).
A limitation of the convertibility of heat into work results from the second law of thermodynamics.
Energy balance for any open system
Applied to the open system, the first main clause is formulated differently mathematically.
In the open system, in addition to the mechanical work on the movable system limit (volume change work e.g. on the piston in a cylinder), the displacement work of the mass flows at the inlet and outlet flow beyond the specific system limit . They are the product of pressure and volume. Instead of the internal energy, the open system therefore uses the enthalpies that contain this term.
The balance for an unsteady system in which both the mass content and the energy content change over time is:
There are:
- : the change in the energy content in the system over time (energy content = internal energy + kinetic energy + potential energy).
- : the heat flow over the system boundary.
- : the work flow ( technical work ) beyond the system boundary.
- : the mass flow into the system.
- : the mass flow from the system
- : the specific enthalpy
- : the specific potential energy (with = height above the reference level and = acceleration due to gravity )
- : the specific kinetic energy (with = speed).
Energy balance for a steady state
- For a steady state: and
- or, one summarizes the external energies in a single term:
- additionally adiabatic (e.g. steam turbine):
Here is the shaft power of the machine. Since energies given off by the system are defined negatively in thermodynamics, the power of a turbine becomes negative from this equation. In practice, the sign is therefore changed. In simplified calculations, one also neglects the external energies.
Energy balance for circular processes
Since the working medium returns to its initial state after it has run through a cycle, the balance is simplified, there are no changes to the state variables, and the process variables heat and work remain. As will be explained in connection with the 2nd law, not only can heat be supplied, which is completely converted into work, but heat must also be removed. The simple balance equation is:
The circle integral adds up all heat flows. They are positive when they enter the system and negative when they leave. is the entire work of the cycle. It is negative when given away.
The relationship is also often written with the amounts of heat:
- ,
whereby the heat dissipation becomes more clearly recognizable.
Second law
The second law of thermodynamics makes statements about the direction of processes and the principle of irreversibility . The definition of the thermodynamic temperature and the state variable entropy can be derived from the second law. Also follows from the second law of thermodynamics the distinction between exergy and anergy and the fact that the efficiency of a heat engine cannot exceed the Carnot efficiency .
The second law of thermodynamics in the formulation of Clausius reads:
- " There is no change of state the only result of which is the transfer of heat from a body at a lower temperature to a body at a higher temperature."
To put it more simply: heat cannot by itself pass from a body with a lower temperature to a body with a higher temperature. This statement seems superfluous at first, because it corresponds to everyday experience. Nevertheless, it is equivalent to all other, less “obvious” statements, because all contradictions to the other statements can be traced back to a contradiction to this one.
The second law of thermodynamics in the formulation of Kelvin and Planck reads:
- “ It is impossible to construct a periodically operating machine that does nothing more than lift a load and cool a heat reservoir. "
The first law would not contradict the assumption that it is possible to supply a constant flow of heat to an engine - whatever it may be - that it emits completely as mechanical or electrical power. Such a machine is called a perpetual motion machine of the second type. A corresponding formulation of the second main clause reads:
- A perpetual motion machine of the second kind is impossible.

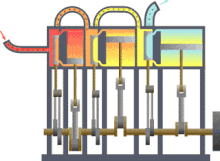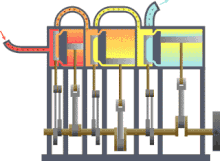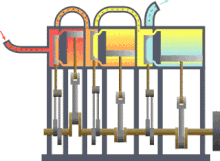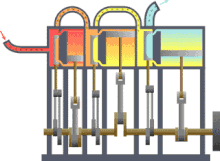
Assuming that there were this independent engine of a heat sink for heat dissipation, so the environment, z. B. the sea water, heat can be withdrawn and converted into mechanical work. You could also extract the heat from a reservoir or container, as shown in the picture on the right, and use the converted energy to drive a heat pump that uses a reversible Carnot process to convey heat from another container with a lower temperature to the former with a higher temperature. The amount of heat fed into the warmer container would then be greater than that absorbed by the engine, because the energy released by the heat pump consists of the sum of absorbed heat and drive work. If you imagine the system boundary around both machines including the two heat containers, then within this closed system - i.e. without energy and material exchange with the environment - heat would ultimately have flowed from a colder to a warmer body. This contradicts the first statement. In principle, the same contradiction also arises with the assumption that a prime mover could be built that has a greater degree of efficiency than a machine operating with a Carnot process. This machine would also take less heat from the warmer container than the Carnot heat pump it drives feeds in there. The corresponding statement form of the second main clause is:
- There is no heat engine that has a higher efficiency than the Carnot efficiency formed from these temperatures at a given average temperature of the heat supply and heat removal
Mentioning the mean temperatures is important because, as a rule, a heat reservoir changes its temperature through the addition or removal of heat.
It is not just any temperature (e.g. not the degree Celsius or Fahrenheit temperature) of the system, but rather the “ absolute ” defined by the equation of state of the “ideal gas” or, better, by the efficiency of the Carnot process just given Temperature "(Kelvin).
Immediately in this context, the following can be further formulated:
- All reversible heat and power processes with the same mean temperatures of heat supply and heat removal have the same efficiency as the corresponding Carnot process.
and:
- All irreversible heat and power processes are less efficient.
With the term definitions established in modern thermodynamics ( heat , work , internal energy , state variable , process variable , adiabatic ...) and with the systematic classification of the systems , the state variable entropy introduced by Clausius can be used to create a generally valid for all closed systems and processes in open systems Statement of the second law can be given in mathematical form. In open systems, the balance refers to a fluid particle that moves through the system and can be viewed as a closed moving system (see above) .
This is the work that is dissipated within the system (work that does not reach the outside, but increases the internal energy as a result of friction, throttling or impact processes). She is always positive. The corresponding term in the equation is called “produced entropy” - in contrast to the first term, which is called “transported entropy” and can also be negative.
For the adiabatic system with, this results in:
- In a closed adiabatic system, the entropy cannot decrease, it usually increases. It only remains constant in reversible processes.
Here, too, the equivalence with the first statement by Clausius is easy to see. An automatic heat flow from the colder to the warmer container in the arrangement outlined above would mean that the entropy of the colder container (lower temperature in the denominator) decreases more than that of the warmer container increases, i.e. H. the total entropy in the system decreases, which is not possible.
All spontaneous processes are irreversible. There is always an increase in entropy. Examples are the mixing of two different gases and the flow of heat from a hot to a cold body without generating work. The restoration of the (often called “ordered”) initial state then requires the use of energy or information (see Maxwell's demon ). Reversible processes are not associated with an increase in the total entropy and therefore do not take place spontaneously. Through the theoretical description of spontaneously occurring processes, the second law of thermodynamics distinguishes a direction of time that corresponds to our intuitive world of experience (see the example below).
With the contexts described, the following sentence is also a statement of the second main clause:
- The thermal energy of a system consists of an exergy part and an anergy part , the exergetic part disappearing when the system is transferred into the surrounding state.
Exergy is the portion of thermal energy that can be converted into other forms of energy . If a body or system with a state that deviates from that of its surroundings is reversibly brought into the surrounding state, its exergy is given off as work. The heat that a body (e.g. hot flue gas in the boiler of a power plant) gives off when it cools down to ambient temperature can theoretically be used to convert it into work via a sequence of differential Carnot processes, as shown in the picture on the right will. The exergetic portion results from adding up the differential (pink) surface portions above the ambient temperature .
The heat sink for these processes to absorb the anergy (blue area below ) is the environment. If a gas in its initial state has not only a higher temperature but also a higher pressure than the ambient state, the total exergy consists not only of the exergetic part of the heat, but also of a part of volume work .
The thermal efficiency of the real heat engine is therefore always less than 1 and - due to the process control specified by the machines and the inevitable dissipative effects - also always smaller than that of the ideal heat engine:
where is the ambient temperature and the mean temperature of the heat input. It results when the yellow area of the exergy is replaced by a rectangle of the same area above the line of the ambient temperature.
The second law therefore has considerable technical implications. Since many machines that supply mechanical energy generate it via a detour from thermal energy (e.g. diesel engine : chemical energy, thermal energy, mechanical energy), the limitations of the 2nd law always apply to their degree of efficiency. In comparison, hydropower plants, which do not require an intermediate stage via thermal energy for the conversion, offer significantly higher degrees of efficiency.
Third law
This main theorem was proposed by Walther Nernst in 1906 and is also known as the Nernst theorem . It is of a quantum theoretical nature and is equivalent to the statement that the zero point of absolute temperature cannot be reached:
- It is not possible to cool a system down to absolute zero.
As the temperature approaches absolute zero ( ), the entropy becomes independent of thermodynamic parameters. This goes against a fixed limit value :
The constant entropy at can be represented as , where the Boltzmann constant and the number of possible micro-states are in the ground state (degeneracy). For example, for an atomic crystal, the atoms of which have two possible spin positions in the energy ground state .
The following applies to all physicochemical reactions in which the participating substances are ideal crystalline solids at absolute zero:
There is only one possibility for realizing ideal solid at absolute zero, .
The above statements can be strictly proven using methods of quantum statistics.
In the context of classical thermodynamics, the behavior of the entropy at absolute zero can also be derived from the following alternative formulation of the third law:
- If the composition of two thermodynamic systems is an isolated system, then any exchange of energy in any form between the two systems is restricted.
Energy calculations in thermodynamics
The energy balance is very important in thermodynamics.
In the case of a phase transition (solid-liquid-gas) or mixtures (salt in water, mixture of different solvents), conversion energies ( melting enthalpy , evaporation enthalpy , sublimation enthalpy) or conversion enthalpy are required or are released in the opposite direction. In the case of a chemical conversion of substances, heats of reaction or enthalpies of reaction can be released or, vice versa, must be supplied.
To calculate the heat of reaction released during the conversion of substances, the corresponding reaction equation with the associated stoichiometric factors is first set up. The standard enthalpies of formation of the individual substances are recorded in tables for 25 ° C. The sum of the enthalpies of the products is added according to the stoichiometric factors and the enthalpies of the starting materials are subtracted from this ( Hess's heat law ).
The enthalpy of reaction or transformation that is released into the environment during a chemical reaction or phase change has a negative sign. If an energy supply from the environment is necessary for a phase change or a chemical conversion, this has a positive sign.
The state variable enthalpy is, in detail:
The free enthalpy is
By forming the total differential of the free enthalpy and then integrating it, it can be calculated whether a chemical conversion is possible.
If the difference between the free energies of the products and the starting materials ( educts ) is negative , a phase change or a material conversion is possible. If the difference in the free enthalpy of a reaction or a phase transition is negative, a reaction takes place - as long as it is not kinetically inhibited - up to a point at which it becomes. The law of mass action is a special case of such an equilibrium. If the difference in free enthalpy is positive , a reaction or phase change is impossible.
In 1869, Marcellin Berthelot still believed that chemical transformations were only possible when heat was released. Conversions and reactions are now known in which no heat of reaction or heat of conversion is released. This is due to the entropy term
Examples:
- When Glauber's salt is dissolved in water, the solution becomes colder than the environment. The enthalpy term is positive, however, the disorder, i. H. the entropy, by dissolving too.
- When melting a block of ice, heat is required to transform the phase from solid to liquid. The temperature of the water does not rise, although heat is supplied from the surroundings. The disorder, the entropy of the molecules is greater in the liquid state than in the solid state.
- When coal and carbon dioxide are converted to carbon monoxide, the enthalpy of reaction is positive. Due to the reaction entropy, the equilibrium (see: Boudouard equilibrium ) can be shifted towards carbon monoxide at high temperatures.
Thermodynamics of irreversible processes
In addition to classical equilibrium thermodynamics, non-equilibrium thermodynamics or the thermodynamics of irreversible processes were developed in the 20th century . For this work, the Nobel Prize in Chemistry was awarded to Lars Onsager in 1968 and Ilya Prigogine in 1977 .
Classical thermodynamics only makes the qualitative statement about non-equilibrium processes that these are not reversible, but its quantitative statements are limited to systems that are always globally in equilibrium or only deviate from it incrementally. In contrast, non-equilibrium thermodynamics deals with systems that are not in global thermodynamic equilibrium, but deviate from it. Often, however, a local thermodynamic equilibrium is still assumed.
An important result of non-equilibrium thermodynamics is the principle of minimum entropy production for open systems that deviate only slightly from thermodynamic equilibrium. This is the realm of so-called linear irreversible thermodynamics . In a unified formal framework, it describes linear relationships between rivers and their corresponding forces . These forces are usually understood as gradients of a scalar quantity and the flows are described by well-known linear laws of nature, such as Ohm's law (current flow), Fick's law ( diffusion ), Fourier's law ( heat conduction ) or the kinetics of a chemical reaction ( reaction rate ). By balancing the entropy, which includes the production of entropy in the system and the entropy flowing across the system boundaries, the second law shows the invariance of these laws. The example of heat conduction shows that only a heat flow from hot to cold is compatible with thermodynamics, and that heat conductivity must always be a positive variable. The mathematical analysis also shows that a thermodynamic force (e.g. temperature difference or voltage difference) in a system causes an additional indirect flow (example: electrical current flow caused by heat conduction ( Seebeck coefficient ), or heat flow caused by an electrical current flow ( Peltier coefficient )). Lars Onsager showed that the influences between rivers and the forces that do not correspond to them are equally large ( reciprocity relationships ). Since the entropy balance in a closed system must always be positive, it also follows: The size of the cross effects is always significantly smaller than the direct effects. For the example with the two forces, the cross effects (Peltier coefficient and Seebeck coefficient) correspond to a maximum of twice the square root of the products of the coefficients of the two direct effects (electrical and thermal conductivity).
If an open system deviates strongly from equilibrium, the nonlinear non - equilibrium thermodynamics comes into play. An important result in this area is the stability criterion by Ilya Prigogine and Paul Glansdorff , which indicates the conditions under which the state with the minimum entropy production becomes unstable and a system can adopt a higher-order structure with simultaneous entropy export . In this area, so-called dissipative structures can arise spontaneously , which have been confirmed experimentally (for example Bénard cells ). Since biological processes are also to be found in this non-linear area, this result is particularly important with regard to the development of life.
representative
- Pierre Prévost ( Prévost's theorem )
- James Prescott Joule
- Nicolas Léonard Sadi Carnot
- Julius Robert von Mayer
- Hermann von Helmholtz
- William Thomson, 1st Lord Kelvin
- James Clerk Maxwell
- Ludwig Boltzmann
- Joseph Louis Gay-Lussac
- Robert Boyle
- Edme Mariotte
- Rudolf Clausius
- Josiah Willard Gibbs
- Guillaume Amontons
- Lorenzo Romano Amedeo Carlo Avogadro
- Jacques Charles
- Ilya Prigogine
- André Bardow
See also
- Equilibration
- Isothermal , isochor
- Kinetic gas theory
- Leidenfrost effect
- Maxwell-Boltzmann distribution
- Nernst theorem
- Phase (matter) , phase diagram
- quasi-static
- Sankey diagram
- Statistical Physics
- Thermal equation of state of ideal gases
- Thermodynamic potential
- Triple point
- Van der Waals equation , Van der Waals radius
- Heat transfer
- Recurrence sentence
literature
Generally
- Herbert B. Callen: Thermodynamics and an Introduction to Thermostatistics . 2nd Edition. Wiley Text Books, New York 1985, ISBN 0-471-86256-8
- Constantin Carathéodory : Investigations on the fundamentals of thermodynamics In: Mathematische Annalen , 67: 355–386, 1909. Carathéodory's publication ( first axiomatically strict justification of thermodynamics ) received great attention from Max Planck and Max Born .
- Ulrich Nickel: Textbook of Thermodynamics. A clear introduction. 3rd, revised edition. PhysChem, Erlangen 2019, ISBN 978-3-937744-07-0 .
- Max Planck: Lectures on Thermodynamics.
-
Karl Stephan , Franz Mayinger: Thermodynamics. Basics and technical applications. 2 volumes, Springer
- Volume 1: One- component systems . 15th edition. 1998, ISBN 3-540-64250-1
- Volume 2: Multicomponent Systems and Chemical Reactions . 14th edition. 1999, ISBN 3-540-64481-4
- André Thess: The entropy principle - thermodynamics for the dissatisfied . Oldenbourg, 2007, ISBN 978-3-486-58428-8
- Gerd Wedler: Textbook of physical chemistry . Verlag Chemie, Weinheim 1982, ISBN 3-527-25880-9
- Herbert Windisch: Thermodynamics - A textbook for engineers . 4th, revised edition. Munich: Oldenbourg Wissenschaftsverlag 2011, ISBN 978-3-486-70717-5
Chemical thermodynamics
- Wolfgang Wagner: Chemical Thermodynamics . 4th edition. Akademie Verlag, Berlin 1982
- Hans-Heinrich Möbius , Wolfgang Dürselen: Chemical Thermodynamics . 5th edition. VEB Verlag for basic industry, Leipzig 1988, ISBN 3-342-00294-8
- Hans-Werner Kammer, Kurt Schwabe: Introduction to the thermodynamics of irreversible processes . Akademie Verlag, Berlin 1984
- Hans-Joachim Bittrich: Guide to chemical thermodynamics . Verlag Chemie, Weinheim 1971, ISBN 3-527-25019-0
- Physical chemistry # General textbooks
- G. Kortüm: Introduction to chemical thermodynamics . 5th edition. Verlag Chemie, Weinheim 1966
- Hans Kelker: Applied Chemistry . Fischer Lexikon, Fischer Taschenbuch, Frankfurt a. M. 1977, ISBN 3-436-02460-0 , pp. 287-292
History of thermodynamics
- Ervin Szücs: Dialogues about technical processes , VEB Fachbuchverlag Leipzig, 1976
- Handbook of Experimental Chemistry, Secondary Level II , Volume 7: Chemical Energetics , pp. 1-13, Aulis Verlag Deubner, Cologne
- Hans Joachim Störig: Small world history of science 2. Fischer paperback, Frankfurt a. M. 1982, pp. 88-96; Parkland, Cologne 2004, ISBN 3-89340-056-7
Statistical Thermodynamics
Technical thermodynamics
- Fran Bošnjaković, KF Knoche : “Technical Thermodynamics” Part 1, 8th corrected edition 1998, Steinkopff Verlag Darmstadt, ISBN 978-3-642-63818-3
- Hans D. Baehr, S. Kabelac : Thermodynamics, Fundamentals and Technical Applications 13., revised. and exp. Ed., Springer Verlag, 2006, ISBN 3-540-32513-1
- Hans D. Baehr, Karl Stephan: Heat and mass transfer 5., revised. Ed., 2006, Springer Verlag, ISBN 3-540-32334-1
- Günter Cerbe, Gernot Wilhelms: Technical Thermodynamics. Theoretical foundations and practical applications. 14th edition, Hanser Fachbuchverlag, June 2005, ISBN 3-446-40281-0
- N. Elsner, A. Dittmann: Fundamentals of Technical Thermodynamics , Vol. 1 and 2, Akademie Verlag, Berlin 1993
- EP Hassel, TV Vasiltsova, T. Strenziok: “Introduction to Technical Thermodynamics”; FVTR GmbH; Rostock 2010; ISBN 978-3-941554-02-3
- Heinz Herwig, Christian H. Kautz: Technische Thermodynamik , ed., 2007, Pearson Studium, ISBN 978-3-8273-7234-5
- Dirk Labuhn, Oliver Romberg: Don't panic about thermodynamics! , 1st edition, Vieweg, Braunschweig 2005, ISBN 3-8348-0024-4
- Klaus Langeheinecke, Peter Jany, Eugen Sapper: Thermodynamics for Engineers . 5th edition. Vieweg Verlag, Wiesbaden 2004, ISBN 3-528-44785-0
- W. Schneider, S. Haas: Repetitorium Thermodynamik . Oldenbourg Verlag, 2004, ISBN 978-3-486-57614-6
- Volker Sperlich: Exercises on thermodynamics with Mathcad , Fachbuchverlag Leipzig 2002, ISBN 3-446-21603-0
- Peter Stephan, Karlheinz Schaber, Karl Stephan, and Franz Mayinger Thermodynamics 1. Single-substance systems. Basics and technical applications , Springer Verlag, Berlin, November 1998, 15th edition, ISBN 3-540-64250-1
- Wolfgang Wagner: Properties of Water and Steam. / State variables of water and water vapor , Springer Verlag, Berlin, 1st edition, August 2002, ISBN 3-540-64339-7
- Klaus Lucas: Thermodynamics. / The basic laws of energy and material conversion , Springer Verlag, Berlin, 5th edition, 2006, ISBN 3-540-26265-2
Thermodynamics in Biology
- Dieter Leuschner: Thermodynamics in Biology. An introduction. Akademie Verlag, Berlin 1989, ISBN 3-05-500487-6
Web links
- What is entropy from the alpha-Centauri television series(approx. 15 minutes). First broadcast on Aug 4, 2004.
- Online refresher course on thermodynamics - with videos - (experimental physics) - University of Würzburg
- University of Duisburg-Essen, basics of technical thermodynamics with exercises and solutions, + computational Mathcad files
- University of Duisburg-Essen, basics of technical thermodynamics (PDF; 2.6 MB)
- Günter Jakob Lauth (SciFox): Introduction to chemical thermodynamics . Lecture series, video recordings, 2013/2014.
- Comprehensive collection of formulas for thermodynamics 1 at TUM (PDF, less than 3 MB). The topics include: First and second law, equations of state of ideal gases, real fluids and cycle processes.
Individual references and comments
- ^ Wilhelm Gemoll: Greek-German school and hand dictionary. Munich / Vienna 1965.
- ↑ Is referred to as "basic science of technology" (Baehr, Kabelac: Thermodynamik. 15th edition, p. V, as "specialist modules of engineering", "engineering science" and "subfield of physics" (Barth: Thermodynamik für Maschinenbauer. 2011, S. V, 2.)
- ↑ Herwig Kautz: Technical Thermodynamics. Pearson Studium, Munich, 2007, p. 20.
- ↑ Windisch Thermodynamik - A textbook for engineers. Oldenbourg, 3rd edition, 2008, p. 2 f.
- ↑ Bökh, Stripf: Technical Thermodynamics. Springer, 2nd edition, 2015, p. 1.
- ↑ Herwig Kautz: Technische Thermodynamik , Pearson Studium, Munich, 2007, p. 18.
- ↑ Baehr, Kabelac: Thermodynamik , Springer, 15th edition, 2012, SV
- ↑ Christoph Strunk: Modern Thermodynamics - From Simple Systems to Nanostructures , Ge Gruyter, 2015, p. V f.
- ↑ Mihály Németh-Csóka: Thermal management of electrical machines , Springer, https://www.springer.com/de/book/9783658201326
- ↑ Frank-Michael Barth: Thermodynamics for mechanical engineers , Oldenbourg, Munich, 2012, p. 2 f.
- ↑ Hans Dieter Baehr, Stephan Kabelac: Thermodynamics - Fundamentals and technical applications , Springer, 15th edition, p. 10.
- ↑ Handbook of Experimental Chemistry, Upper Secondary Level II. Volume 7: Chemical Energetics. Aulis Verlag Deubner, Cologne, p. 1.
- ↑ Hans Joachim Störig: Small world history of the sciences. Vol. 2. Fischer Taschenbuch, 1982, p. 91.
- ↑ Gerd Wedler: Textbook of Physical Chemistry. Verlag Weinheim, 1982, p. 59.
- ↑ Hans Joachim Störig: Small world history of the sciences. Vol. 2. Fischer Taschenbuch, 1982, pp. 93, 1280.
- ↑ Lorenz: Outline of the historical development of the theory of heat. In: Journal for the refrigeration industry. 1904, issue 8, p. 144.
- ↑ H. von Helmholtz: The Thermodynamics of chemical processes (1882). In: Scientific papers by Hermann Helmholtz. Volume 2. JA Barth, Leipzig 1882, pp. 958-978.
- ↑ Handbook of Experimental Chemistry, Upper Secondary Level II. Volume 7: Chemical Energetics. Aulis Verlag Deubner, Cologne, p. 11.
- ↑ Handbook of Experimental Chemistry, Upper Secondary Level II. Volume 7: Chemical Energetics. Aulis Verlag Deubner, Cologne, p. 9.
- ^ Ingo Müller: A History of Thermodynamics . 1st edition. Springer-Verlag, Berlin Heidelberg 2007, ISBN 978-3-540-46226-2 (English).
- ↑ An article about Richard Towneley is currently only available on Wikipedia
- ↑ Walter Conrad (ed.): History of technology in spotlights . 1st edition. Bibliographisches Institut & FA Brockhaus AG, Mannheim 1997, ISBN 3-411-07741-7 , 3.2.2 Gas engine / Otto engine.
- ↑ a b Klaus Langeheinecke (eds.), Peter Jany, Gerd Thieleke: Thermodynamics for engineers. 6th edition, Friedr. Vieweg & Sohn Verlag, Wiesbaden 2006, Section 2.1 Systems and Energies .
- ↑ See section 15.2 “Joule-Thomson effect or throttle effect” in Bošnjaković / Knoche “Technical Thermodynamics Part 1”, 8th edition, Steinkopff-Verlag Darmstadt 1998, ISBN 978-3-642-63818-3 .
- ^ According to Baehr / Kabelac "Thermodynamik", 13th edition, Springer-Verlag 2005, ISBN 3-540-23870-0 .
- ↑ See section 1.4.3 in Baehr / Kabelac “Thermodynamik”, 13th edition, Springer-Verlag 2005, ISBN 3-540-23870-0 .
- ↑ Hans-Heinrich Möbius, Wolfgang Dürselen: Chemical Thermodynamics.
- ↑ In this chapter the concepts of the Karlsruhe physics course are used explicitly , in which the entire physics is based on the concept of "currents" and extensive basic quantities are preferred. Another concept is used, for example, by W. Döring , who in his Thermodynamik-Bändchen ("Göschen-Verlag") uses the (intensive) so-called "pressure " in addition to the usual (extensive) "volume work" (energy increase by compressing a gas volume with a moving punch) -Work "(energy increase through vertical transport of weights on the top of a solid cube container for the fluid system) is used. Extensive and intensive work are different, but the preference of the respective aspect is a matter of taste, about which there is just as little arguable as the preference for force or impulse as a basic variable in mechanics: there is equivalence in the following sense: The first law of the Thermodynamics can be formulated on the one hand in the usual form , on the other hand in the different but equivalent form .
- ^ Quote from Max Planck , after entry on main clauses. In: Römpp Online . Georg Thieme Verlag, accessed on August 24, 2011.
- ↑ M. Heidrich: Bounded energy exchange as an alternative to the third law of thermodynamics . In: Annals of Physics . 373, 2016, pp. 665-681. bibcode : 2016AnPhy.373..665H . doi : 10.1016 / j.aop.2016.07.031 .