Thermoelectricity

Under thermoelectricity one understands the mutual influence of temperature and electricity and their conversion into one another. Seebeck effect (also thermoelectric effect), Peltier effect and Thomson effect each describe a reversible interaction between the two physical quantities .

Effects

Seebeck effect

A simple circuit that shows the Seebeck effect. Materials A and B of the electrical conductor meet at points T ₁ and T ₂ .

An electrical voltage generated by the Seebeck effect is applied to the resistor. This causes an electric current to flow through the resistor.

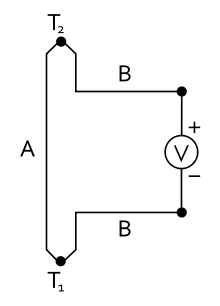
According to the Seebeck effect, named after Thomas Johann Seebeck , an electrical voltage of magnitude arises in a circuit made up of two different electrical conductors when there is a temperature difference between the contact points

${\displaystyle U=\int _{T_{1}}^{T_{2}}\left(S_{\mathrm {B} }(T)-S_{\mathrm {A} }(T)\right)\,\mathrm {d} T.}$

Here and are the temperatures of the contacts between materials A and B. The Seebeck coefficients and are material constants that also depend on the temperature. Alternatively, a is used as a symbol . The Seebeck coefficient has the dimension of an electrical voltage per temperature difference (volt / Kelvin). The typical order of magnitude for metals at room temperature is 10 µV / K. ${\displaystyle T_{2}}$ ${\displaystyle T_{1}}$ ${\displaystyle S_{\mathrm {A} }}$ ${\displaystyle S_{\mathrm {B} }}$ ${\displaystyle \alpha }$

For small temperature differences and constant values ​​for the Seebeck coefficients, the formula is simplified to

${\displaystyle U=(S_{\mathrm {B} }-S_{\mathrm {A} })\cdot (T_{2}-T_{1})}$

In the thermoelectric voltage, only the difference between the Seebeck coefficients occurs. Since it is difficult to determine individual (absolute) Seebeck coefficients (see Thomson effect), platinum was chosen as the reference element for tabulated numerical values ​​(see thermoelectric series ).

The Seebeck effect only describes the creation of this tension. A current flow caused by external wiring is not part of this effect and only follows from Ohm's law .

Historical

Thomas Johann Seebeck discovered by chance that an electrical voltage is created in a circuit made of two different metals (e.g. in the form of a rod) if there is a temperature difference between the two connecting points of the rods . He was able to prove that electric current was flowing through the magnetic field that occurred with the help of the typical deflections of a compass needle placed in him. Seebeck used this effect in 1821 in a first thermocouple .

Explanation

The voltage is created by thermal diffusion currents in a material. Considering only one material with a temperature gradient provides a sufficient explanation. Two different metals are needed for measurement purposes. At the hot end of the conductor there are more high energy electrons and fewer low energy electrons (below chemical potential). By diffusion, high-energy electrons move to the cold end and electrons with little energy move in the opposite direction. This describes the heat conduction through electrons. Any imbalance in the currents is compensated for by an electric field, since no current can flow in an open circuit. The resulting voltage (integral of the electric field) is the Seebeck voltage.

It is determined by the dependence of the mobility and number ( density of states ) of the electrons on the energy. The dependence of the mobility on the energy depends sensitively on the type of scattering of the electrons. Correspondingly, even relatively small impurities can have a very strong influence on the thermal power. The driving force for diffusion is proportional to the temperature difference. As a rough trend, one therefore expects an increase in the Seebeck coefficient roughly proportional to the temperature for metals.

A special case is the so-called electron drag. At low temperatures of about 1/5 the Debye temperature , the phonons are slowed down mainly by collisions with electrons. The phonons pull the electrons with them towards lower temperatures. As a result, the thermoelectric effects can be somewhat greater in this temperature range than is otherwise expected. At higher temperatures, flip processes for the scattering of the phonons become more important and the effect becomes smaller.

Numerical values

Thermal voltages of common thermocouples

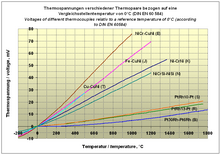
Seebeck coefficients of some metals and alloys relative to platinum (see thermoelectric series ):

material	α in µV / K at 273 K.
Bismuth	−72
Constantan	−35
nickel	−15
platinum	−00
carbon	−03
aluminum	−03.5
Rhodium	−06th
copper	−06.5
gold	−06.5
silver	−06.5
iron	-19th
Nichrome	-25th

In order to obtain the absolute Seebeck coefficient of the materials specified here, the absolute Seebeck coefficient of platinum (between −4.04 µV / K at 273 K and approx. −5 µV / K at 300 K) must be added.

Peltier effect

A Peltier element with semiconductors (N and P) powered by a battery

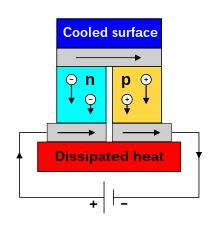
With the Peltier effect, applied to the Peltier element , the situation is opposite to that of the Seebeck effect - an electrical current flow causes a change in the heat transport. However, while the Seebeck effect describes the creation of a voltage, the Peltier effect occurs exclusively through the flow of an electrical current. Both effects always occur in a thermocouple through which a current flows, but the Peltier effect is difficult to detect with metallic thermocouples. Jean Peltier made the discovery in 1834, thirteen years after the discovery of the Seebeck effect.

When an electric current I flows to a contact from a material A into a material B, a heat source of the size is created:

${\displaystyle {\dot {Q}}=\Pi _{\mathrm {AB} }I=\left(\Pi _{\mathrm {A} }-\Pi _{\mathrm {B} }\right)I}$

The Peltier coefficients are material constants that generally depend on the temperature. ${\displaystyle \Pi _{\mathrm {B} },\Pi _{\mathrm {A} }}$

Depending on the sign of the current, heat can be released or removed. As a rule, one contact becomes warm and the other cold.

Explanation

To explain the Peltier effect, it is sufficient to link it to the Seebeck effect via the Thomson relations. But there is also a relatively clear, direct explanation for the Peltier effect: Moving electrons always transport energy as well as charge e. How much that is on average depends, among other things, on how the number of charge carriers and the scatter rate depend on the energy. Higher-energy electrons contribute more to the electricity, but at the same time also transport more energy. When moving from one material to another, the energy transported with the electrons changes. The difference is released or absorbed as heat at the contact point (Peltier effect). The energy transported with the electron corresponds precisely to the Peltier coefficient. In semiconductors, the distance between the chemical potential and the band edge is an essential part of this. In particular, this explains why the thermoelectric effects in semiconductors are often much greater than in metals.

Thomson effect

(not to be confused with the Joule-Thomson effect or the Gibbs-Thomson effect or the Thomson effect as a galvanomagnetic effect )

The Thomson effect, named after William Thomson, 1st Baron Kelvin 1856, describes the changed heat transport along a current-carrying conductor in which there is a temperature gradient .

Every current-carrying conductor with a temperature difference between two points will, depending on the metal, transport either more or less heat than would be the case without current flow due to the thermal conductivity. However, this effect is superimposed on the heating of the electrical conductor by the current due to its resistance and is therefore difficult to detect.

A current density in a homogeneous conductor causes a heat output per unit volume of ${\displaystyle J}$

${\displaystyle q=\rho J^{2}-\mu J{\frac {\mathrm {d} T}{\mathrm {d} x}}}$

where are the resistivity of the material, the temperature gradient in the conductor and the Thomson coefficient. ${\displaystyle \rho }$ ${\displaystyle \mathrm {d} T/\mathrm {d} x}$ ${\displaystyle \mu }$

The first term is irreversible Joule warming . The second term is the Thomson heat , the sign of which changes with the direction of the current. ${\displaystyle \rho J^{2}}$

There is as yet no technical application for the Thomson effect. The absolute thermoelectric coefficients can be determined via the Thomson effect by integration via the temperature.

Thomson relations

Seebeck, Peltier and Thomson effects are not independent of one another, but have a common cause. As early as 1854 Thomson found two relationships between the corresponding coefficients, which are called Thomson relations (sometimes also Kelvin relations):

${\displaystyle \Pi =S\cdot T}$

${\displaystyle \mu =T\cdot \mathrm {d} S/\mathrm {d} T}$

Are there

• ${\displaystyle \Pi }$ the Peltier coefficient
• S is the Seebeck coefficient
• T is the absolute temperature
• ${\displaystyle \mu }$ the Thomson coefficient.

The second equation predicted the Thomson effect.

Anisotropic materials

In the general case of an anisotropic material, the electrical and thermal conductivity can be tensor quantities . The same applies to the thermoelectric coefficients. So it is with z. B. possible that heat is released when the current at a grain boundary changes direction relative to the crystal axes. This is called the Bridgman effect , after the American physicist PW Bridgman .

As a rule, the directional dependency is neglected. Many materials are actually isotropic with regard to conductivity because of their cubic symmetry.

Applications and effects

Thermocouples made of metals only inefficiently convert thermal energy into electrical energy and are therefore almost only used as thermocouples for temperature measurement. To measure small temperature differences, many thermocouples can be connected electrically in series, e.g. B. in the thermopile for measuring radiation.

The thermal voltages occur as a disruptive effect when measuring small DC voltages. Here, attention must be paid to small temperature gradients and a suitable choice of material.

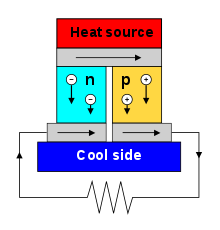
By using semiconductor materials (for materials and structure, see Peltier element ), the conversion efficiency can be increased to up to 3–8% and is thus well below the Carnot efficiency . This can be used to build thermoelectric generators. Such generators or converters find u. a. in isotope batteries and convert heat energy into electrical energy without any moving parts without wear.

The Peltier effect can be used in Peltier elements for cooling and temperature control. Because of the relatively poor efficiency, this is limited to rather small applications. The good scalability, controllability and reliability are advantageous. In terms of structure and the required material properties, Peltier elements and thermoelectric generators are similar.

The technical application for cooling is limited by the phononic heat conduction, it causes a heat flow in the opposite direction, especially in the case of large temperature differences, which cancels the heat flow caused by the current flow from around 70 K. For the same reason, thermoelectric generators only have a low level of efficiency.

There is no technical application for the Thomson effect. The effect is so small that it is difficult to prove it in practice.

Recent developments

The efficiencies of Peltier and Seebeck elements have remained low despite all research programs. The poor efficiency is due to the unwanted heat conduction between the metals or semiconductors. A more recent approach to prevent this is the thermal tunneling process: two metals are separated from one another by a minimal, evacuated gap. The heat conduction via lattice vibrations is completely prevented. However, the vacuum gap is only so wide that individual electrons can "tunnel" it quantum mechanically .

At first sight this interruption of the phononic conduction, i.e. H. the heat conduction via lattice vibrations to be extremely efficient. With a gap size that enables quantum mechanical tunneling, however, the electromagnetic forces are so great that the lattice vibrations are passed on almost unhindered due to electromagnetic coupling.

An efficient decoupling of the lattice vibrations only takes place when the gap size is in the range of the wavelengths . At normal temperatures at which such elements are to be used, the wavelengths of the electromagnetic emissions are in the range from a few hundred nanometers to a few micrometers. However, quantum mechanical tunneling is practically no longer possible with these quantities.

See also

• Pyroelectricity - another method of obtaining electricity from temperature differences
• Galvanomagnetic effects
• Thermomagnetic effects

literature

• Thermal voltages - used a lot and almost always explained incorrectly! In: Physics and Didactics in School and University , 1/4, 2005, pp. 10–22.

Web links

• The Peltier Effect and Other Thermoelectric Phenomena
• J. Jäckle: About the cause of thermal voltage . University of Konstanz, July 1998.
• Caltech Thermoelectrics website
• Gregor Honsel: Energy, the race for electricity from heat . In: Spiegel Online ; Takeover from the Technology Review

Individual evidence

1. ↑ Seebeck Coefficients
2. ^ The Seebeck Coefficient
3. ^ Thermoelectric Effects in Anisotropic Systems: Measurement and Applications . arxiv : 0808.3526