diffusion
Diffusion (Latin diffusio , from Latin diffundere , 'pour out', 'scatter', 'spread out') is the compensation of concentration differences in liquids or gases as a natural physical process due to Brownian molecular movement , which occurs without external influence . Over time, it leads to the complete mixing of two or more substances due to the even distribution of the movable particles and thus increases the entropy of the system. The particles can be atoms , molecules , charge carriers or free neutrons . Usually at least one of the substances is a gas or a liquid , but solids and plasmas can also diffuse into one another.
Working principle
Diffusion is based on the random random movement of particles due to their thermal energy ("thermal movement", see below). In the case of an uneven distribution, statistically more particles move from areas of high to areas of low concentration or particle density than vice versa. This brings about a net macroscopic transport of substances. Diffusion is usually understood to mean this net transport. The term is also used for the underlying microscopic process.
In a closed system , diffusion causes the reduction of concentration differences to the point of complete mixing. The time required for this increases in -dimensional space with the -th power of the distance. Diffusion is therefore mainly effective on nano to millimeter scales; On larger scales, mass transport by flow ( convection ) usually dominates in liquids and gases . Diffusion in solids is also often overlaid by other chemical-physical processes such as absorption , adsorption , resorption and capillary transport .
Diffusion does not depend on the air permeability of a material. In osmosis , small molecules diffuse through a closed membrane that is impermeable to larger molecules. The decisive factor is the diffusivity of the material in relation to the diffusing substance.
Diffusion can be based on various phenomena:
- Collective diffusion is the diffusion of several particles along a concentration gradient, including Fick's laws, for example.
- With self-diffusion, however, individual particles are considered whose behavior u. a. is described by the Einstein relation. The self-diffusion coefficient (subscript S stands for self-diffusion) is a function of time.
- For extremely short times less than the Brownian relaxation time , one speaks of the ballistic regime.
- The short-term diffusion constant prevails for times in the vicinity of the Brownian relaxation time .
- In contrast, the long-term diffusion constant dominates in the Limes of great times .
history
One of the first to systematically carry out diffusion experiments on a larger scale was Thomas Graham . From his experiments on the diffusion of gases he derived Graham's law , named after him :
"It is evident that the diffusiveness of the gases is inversely as some function of their density - apparently the square root of their density."
"It is obvious that the rate of diffusion of gases is the inverse of a function of their density - apparently the square root of their density."
“The diffusion or spontaneous intermixture of two gases in contact, is effected by an interchange in position of indefinitely minute volumes of the gases, which volumes are not necessarily of equal magnitude, being, in the case of each gas, inversely proportional to the square root of the density of that gas. "
“The diffusion or spontaneous mixing of two gases in contact is influenced by the exchange of the position of indefinitely small volumes of the gases which do not necessarily have to be of the same order of magnitude and, in the case of any gas, inversely proportional to the square root of the density of the gas are."
With regard to diffusion in solutions, Graham was able to show that the diffusion rate is proportional to the concentration difference and dependent on the temperature (faster diffusion at higher temperatures). Graham also showed the possibility of separating mixtures of solutions or gases by means of diffusion.
Thomas Graham had not yet been able to determine the fundamental laws of diffusion. Adolf Fick succeeded in doing this only a few years later . He postulated that the law he was looking for must be analogous to the laws of heat conduction that Jean Baptiste Joseph Fourier had determined:
"The dissemination of a dissolved body in the solvent, as long as it takes place undisturbed under the exclusive influence of the molecular forces, proceeds according to the same law which Fourier established for the dissemination of heat in a conductor, and which Ohm has already been so brilliantly successful on the The broadening of electricity (where, of course, it is not strictly correct). "
Fick carried out experiments, the results of which proved the validity of Fick's First Law, which was later named after him. He could only deduce the validity of Fick's second law from the validity of the first. The direct proof failed because of its limited analytical and mathematical possibilities.
At the beginning of the 20th century, Albert Einstein succeeded in deriving Fick's laws from the laws of thermodynamics and thus giving diffusion a secure theoretical foundation. He also derived the Stokes-Einstein relationship for calculating the diffusion coefficient:
"The diffusion coefficient of the suspended substance depends on universal constants and the absolute temperature only on the coefficient of friction of the liquid and on the size of the suspended particles."
Einstein also showed how to capture the motion of a single diffusing particle and thus understand Brownian molecular motion as a fluctuation phenomenon. He calculated the mean square displacement of a particle in time τ for the one-dimensional case . Shortly after Einstein, Smoluchowski also came to practically the same relationship by a different route, and hence this equation is now referred to as the Einstein-Smoluchowski equation .
illustration
An often-cited experiment to illustrate propagation by diffusion is the gradual coloring of lukewarm water with a drop of ink that is put into it, but the water is neither stirred nor shaken. After a while, the ink color will be evenly distributed throughout the water. However, the spread of the ink in the water can also be favored by differences in density and temperature. These influences can be reduced by overlaying a colored liquid with a higher density with a liquid with a lower density and using very viscous liquids, e.g. B. colored syrup and honey. The gradual coloration of the honey then observed can be explained almost exclusively by diffusion, with both syrup diffusing into the honey and honey diffusing into the syrup.
Useful examples
- During sintering , diffusion plays a very important role in the coalescence of the powder components.
- Steel can be hardened by the diffusion of carbon and / or nitrogen or lead to metal dusting .
- In diffusion furnaces, dopants are introduced into the semiconductor material at temperatures around 1000 ° C in order to specifically influence the electrical conductivity or mechanical properties of components in microsystem technology .
- Diffusion plays a central role in technical chemistry . It often occurs here coupled with convection and chemical reactions . Typical applications are reactor and catalyst design . In chemical process engineering, the selective separation of mixtures of substances is often carried out using molecular sieve and / or membrane technology . Both processes are based on "kinetic separation", whereby the differences in the diffusion of the individual substances in nanopores play an essential role and thereby open up control options.
- In semiconductors , electrons move against the field current generated by the voltage source due to a diffusion current.
- With ambipolar diffusion , electrons and ions move in the same direction in the plasma .
- In the building construction , the water vapor diffusion must be taken into account to protect against moisture in order to avoid impermissibly large amounts of condensation. For this purpose, vapor barriers and vapor retarders with defined water vapor diffusion resistance are used.
- In microbiology , diffusion is used in the agar diffusion test .
- In lung breathing , gas exchange between the alveoli and blood occurs through diffusion.
- With what is known as diffusion-ordered spectroscopy (DOSY), the translational mobility of individual molecules can be measured in mixtures and the molecular weight can be determined using the diffusion coefficient .
Physical basics
Diffusion at a certain constant temperature takes place without any additional energy input and in this sense is passive; A distinction is made between diffusion and active transport , especially in biology .
Theoretically, diffusion is an infinitely long process. In terms of measurability, however, it can often be viewed as completed in a finite time.
Thermal movement

The thermal movement on which the diffusion is based can have a very different character depending on the system under consideration. In gases it is straight. interrupted by occasional bumps. The rapid thermal movement of liquid particles causes the much slower Brownian movement of mesoscopic objects that can be observed under the microscope through frequent collisions . Occasional changes of location take place in solids , e.g. B. by exchanging the place of two neighboring particles, or the "wandering" of empty spaces. In the case of charge carriers (e.g. ions , electrons , holes ), however, a drift due to the electrostatic forces is superimposed on the heat movement .
Probability and entropy
The direction of movement of a single particle is completely random. Due to the interaction with other particles, there are constant changes in direction. However, averaged over a longer period of time or over a large number of particles, transport in a certain direction can result, e.g. B. if a jump in a certain direction has a, perhaps only slightly, greater probability . This is the case when there is a concentration difference (also concentration gradient ). A net flow of particles then arises until a steady state, the thermodynamic equilibrium , is established. Usually the state of equilibrium is the uniform distribution, in which the concentration of all particles is equally high at every point in space.
Probability and diffusion - an attempt to explain : Suppose 1000 particles of a substance were only in the right half of a vessel, and 10 particles in the left half; in addition, each particle moves a certain distance in a completely random direction due to Brownian molecular motion. Then follows: The probability that one of the 1000 particles will move randomly from the right to the left half is 100 times greater than the probability that one of the only 10 particles will move from left to right. So after a certain time there is a high probability that net particles will have migrated from right to left. As soon as the probability of migration is the same on both sides, i.e. there are 505 particles on the right and left, there will be no more net mass flow and the concentration will remain the same everywhere (within the framework of statistical fluctuations). Of course, particles still migrate from left to right and vice versa; But since there are now the same number of parts, no difference in concentration can be determined. If you now think of “right” and “left” as particularly small sub-spaces z. B. presents the ink test and all these subspaces at some point all have the same ink concentration, the ink has been evenly distributed.
Systems in which the particles are randomly distributed over the entire volume have a higher entropy than more ordered systems in which the particles prefer to stay in certain areas. Diffusion thus leads to an increase in entropy. According to the second law of thermodynamics, it is a voluntary process that cannot be reversed without external influence.
The greater entropy in a distribution over the entire volume also results from the greater number of distribution patterns (or microstates) that the particles can form if they have more space available. The number of microstates that make up the same macrostate is called its statistical weight . This means that a large-scale distribution also has a higher statistical weight compared to a spatially concentrated arrangement and is therefore also more likely. The entropy ( ) of a macrostate is thus a measure of its probability.
Analogy to heat conduction and conduction of electric current
Diffusion follows laws that are equivalent to those of heat conduction . Therefore, equations that describe one process can be adopted for the other.
Dissolved Particle Diffusion
With a fixed pressure and a fixed temperature , the gradient of the chemical potential is the driving cause of the material flow from the perspective of thermodynamics . The flow is thus:
- : Particle flux density ( flux ) in mol · m −2 · s −1
- : Chemical potential in J · mol −1
- : Length in m
- : a coefficient in mol 2 s kg −1 m −3
For simple applications, the substance concentration can be used instead of the chemical potential . This is more easily accessible than the chemical potential of a substance. For an ideal gas the chemical potential is given by
- ,
for a non-ideal substance, additional excess terms must be taken into account, since particle interactions exist (see chemical potential ).
It is the chemical potential under standard pressure. If the temperature does not explicitly depend on the location, then:
Plugging this into the above equation, you get Fick's first law:
The diffusion coefficient was introduced here. The relationship between the coefficients and is
in which
- : Diffusion coefficient in m 2 s −1
- : Mole concentration in mol · m −3
- : Temperature in K
- : Universal gas constant in J K −1 mol −1
In the case of very low concentrations (individual molecules), this consideration is no longer readily permissible, since classical thermodynamics regards solutions as a continuum . In the case of high concentrations, the particles influence each other so that the concentration equalization takes place more slowly with an attractive interaction and faster with a repulsive one. In these cases, the chemical potential is no longer logarithmically dependent on the concentration.
First Fick's Law
According to Fick's First Law, the particle current density is proportional to the concentration gradient opposite to the diffusion direction. The constant of proportionality is the diffusion coefficient .
The units are for example = mol m −2 s −1 , = mol · m −4 and = m 2 s −1 .
The particle flux density makes a quantitative statement about the (statistical mean) directed movement of particles, i.e. H. how many particles of an amount of substance move per time through an area that is perpendicular to the direction of diffusion, net. The equation given also applies to the general case in which the diffusion coefficient is not constant, but depends on the concentration (but strictly speaking this is no longer the statement of Fick's First Law).
The Nernst-Planck equation can be viewed as an extension of Fick's law .
Fick's second law (diffusion equation)
Continuity equation and differential equation for the one-dimensional case
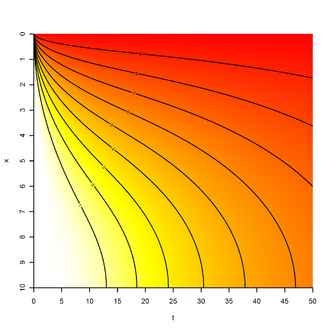
With the help of the continuity equation (conservation of mass)
the diffusion equation results from Fick's First Law
for constant diffusion coefficients results from this
- .
It represents a relationship between temporal and local concentration differences and is therefore suitable for representing unsteady diffusion, in contrast to Fick's first law, which describes a diffusion flow that is constant over time. There are numerous analytical and numerical solutions for this differential equation , which, however, depend heavily on the initial and boundary conditions.
From a mathematical point of view, the diffusion equation is identical to the heat conduction equation , its mathematical properties and possible solutions are dealt with in the article there.
Differential equation for the three-dimensional case
The case of three-dimensional diffusion can be described with Fick's Second Law in its most general form:
with the Nabla operator . From a mathematical point of view, this diffusion equation is also identical to the (three-dimensional) heat conduction equation ; its mathematical properties and solution approaches are dealt with in the article there. Solving this equation is usually time-consuming and, depending on the area under consideration, only possible numerically .
In the stationary case, i.e. H. For
the elliptic partial differential equation results
If, in addition, the diffusion coefficient is isotropic , a differential equation of the Laplace type is obtained .
If, in addition to diffusion, directed transport is also involved, the concentration dynamics are described by the convection-diffusion equation .
Types of diffusion
It is common to distinguish four types of diffusion. The diffusion coefficients differ for different types of diffusion, even if the same particles diffuse under standard conditions .
Self diffusion
If there is no macroscopic gradient in a gas, a pure liquid or a solution, only real self diffusion takes place. Self-diffusion (often referred to as intradiffusion) is the transport of particles within the same substance, for example water molecules in pure water or sodium ions in an NaCl solution. Since it is difficult to differentiate between physically and chemically identical particles, this can only be observed with great effort, so self-diffusion is often approximated with isotopic tracers of the same substance, e.g. 22 Na + for sodium ions. It is assumed that the gradient created by adding the tracer is negligibly small. Self-diffusion is a model for describing Brownian molecular motion. The measured diffusion coefficients can be converted into the mean square displacement of a particle per time period.
Field gradient NMR is a particularly suitable method for measuring self-diffusion coefficients . No isotopic tracers are required here, since physically and chemically identical particles can be distinguished using the nuclear spin precession phase of an atomic nucleus located in the particle. With this NMR technique, self-diffusion coefficients can be determined very precisely in pure liquids as well as in complex, fluid mixtures. The self-diffusion coefficient of pure water has been measured extremely precisely and is therefore often used as a reference value. It is 2.299 · 10 −9 m² · s −1 at 25 ° C and 1.261 · 10 −9 m² · s −1 at 4 ° C.
Tracer diffusion
Tracer diffusion is the diffusion of low concentrations of one substance in a solution of a second substance. Tracer diffusion differs from self diffusion in that a labeled particle of another substance is used as a tracer, e.g. B. 42 K + in NaCl solution. Frequently, radioactive or fluorescent labeled tracer used because it can detect very well this. At infinite dilution, the diffusion coefficients of self and tracer diffusion are identical.
Classic Fickian diffusion
This denotes the diffusion along a relatively strong gradient. With this type of diffusion, an approximation of the diffusion coefficient is best possible.
Counter diffusion
Counter diffusion occurs when there are opposing gradients such that particles diffuse in opposite directions.
Diffusion of gases
In principle, the diffusion of particles in gases does not differ from the diffusion of dissolved particles in liquids with regard to their laws. However, the speed of diffusion (with comparable gradients) is orders of magnitude higher here, since the movement of individual particles in gases is considerably faster. The diffusion of dilute gases in multicomponent systems can be described with the Maxwell-Stefan diffusion model .
Diffusion in solids
In a perfect crystal lattice, every lattice particle swings around its fixed lattice position and cannot leave it. A necessary prerequisite for diffusion in a crystalline solid is therefore the presence of lattice defects . Only through this condition can atoms or ions change their place, and thus mass transfer. Various mechanisms are conceivable:
- The particles “jump” into voids in the lattice, so that voids move through the lattice and a net flow of particles takes place. This mechanism was demonstrated by the Kirkendall effect .
- Smaller particles move through the spaces between the lattices. Compared to diffusion through vacancies, it leads to very high diffusion coefficients. This mechanism has also been proven experimentally.
- Two particles exchange places or there are ring exchanges between several particles. This hypothetical mechanism has not yet been confirmed experimentally.
- If free charge carriers in semiconductors experience sufficient scattering (e.g. from phonons , electrons and impurities ), they also propagate diffusively.
Diffusion in crystals can also be described by Fick's laws. However, diffusion coefficients can depend on the spatial direction ( anisotropy ). The diffusion coefficients, which are scalar in the isotropic case , then become a second- order tensor , called a diffusion tensor . The diffusion path is therefore an important parameter for describing diffusion processes in solids.
In the case of anisotropy, for example, Fick's first law is written as follows:
in that now
is a 3 × 3 matrix called a diffusion tensor (or diffusion matrix ). This matrix is symmetrical and therefore has only six independent components.
The diffusion in non-crystalline ( amorphous ) solids is mechanistically similar to that in crystals, although the distinction between regular and irregular lattice positions is omitted. Such processes can be described mathematically like diffusion in liquids.
Fokker-Planck equation
An additional driving variable due to an existing potential means that the uniform distribution no longer corresponds to the steady state. The theory for this is provided by the Fokker-Planck equation .
Special case: anomalous diffusion
In the diffusion processes described above, which can be described by Fick's diffusion equation, the mean square deflection of the diffusing particles (i.e. the mean distance between the particles and their starting point after time ) increases proportionally to time:
This law follows from the theory of Brownian molecular motion. In cells but other principles may be observed, for example in the movement of macromolecules through the cytoplasm of the cell. This medium, densely populated with organelles and (macro) molecules, leads to a slowed diffusion movement that follows a power law. The following then applies:
The following applies to this slowed movement, which is called subdiffusion . There are also diffusion processes where there is, that is, they are accelerated. These are called superdiffusion .
Special case: facilitated diffusion (biology)
In biology, facilitated diffusion or permeability describes the possibility for certain substances to penetrate a biomembrane more easily than would actually be possible due to their size, charge, polarity, etc. Certain proteins, so-called tunnel proteins, form a tunnel through the cell membrane which, due to its diameter and / or its charge distribution, allows certain substances to pass more easily than through the "closed" membrane (such as ion channels ).
Wrong use of the word diffusion
The terms diffusion and diffusivity are often used in the field of acoustics instead of the German word diffusität . The wrong translation from English contributes to this.
See also
- Reaction diffusion equation
- Eddy diffusion , describes mixing by flow
- Knudsen diffusion , diffusion dominated by boundaries
- Critical layer thickness
- Lévy trial
- Diffusion network
- Diffusivity
- Neutron diffusion
- Transepidermal water loss
literature
- Peter W. Atkins , Charles A. Trapp: Physical chemistry. 3rd corrected edition. Wiley-VCH, Weinheim u. a. 2001, ISBN 3-527-30236-0 .
- Klopfer, H .: Water transport through diffusion in solids. Wiesbaden: Bauverlag 1974 ( abstract ).
- EL Cussler: Diffusion. Mass transfer in fluid systems. 2nd edition. Cambridge University Press, Cambridge u. a. 1997, ISBN 0-521-56477-8 .
- J. Crank: The Mathematics of Diffusion. 2nd revised edition. Oxford University Press, Oxford u. a. 1980, ISBN 0-19-853411-6 .
- Paul Heitjans , Jörg Kärger (Eds.): Diffusion in Condensed Matter. Methods, Materials, Models. Greatly enlarged and completely revised edition. Springer, Berlin a. a. 2005, ISBN 3-540-20043-6 .
- Jörg Kärger (Ed.): Leipzig, Einstein, Diffusion. Leipziger Universitätsverlag, Leipzig, 2007, (3rd edition 2014), ISBN 978-3-86583-176-7 .
- Wilhelm Jost : Diffusion in solids, liquids, gases (= Physical chemistry 1, ISSN 0079-1881 ). 6th printing. Academic Press, New York NY 1970.
- HJV Tyrrell, KR Harris: Diffusion in Liquids. A theoretical and experimental study. Butterworth, London 1984, ISBN 0-408-17591-5 .
Web links
- Fick's Laws of Diffusion , H. Föll, Technical Faculty of the Christian-Albrechts-Universität zu Kiel
- Diffusion in physical material properties (PDF file, 160 kB) at the Leibniz Institute for Solid State and Materials Research
- 3D grid Monte Carlo simulation of diffusion on a vizinally cut car (100) surface by Lars Röntgenzsch
- NetLogo simulation model for teaching (Java applet) by Johannes Kottonau
- Video: Diffusion and Fick's laws - how fast does mass transport go without a flow? . Jakob Günter Lauth (SciFox) 2013, made available by the Technical Information Library (TIB), doi : 10.5446 / 15654 .
Individual evidence
- ↑ Def .: Rompp's chemical dictionary . Franckhsche Verlagsbuchhandlung 1969 and Arnold Arni: Understandable chemistry . Wileg-VCH 1998. ISBN 3-527-29542-9 , p. 224.
- ↑ see e.g. E.g .: KH Beckurts, K. Wirtz: Neutron Physics. Springer 1964, ISBN 978-3-642-87616-5
- ↑ a b Thomas Graham: A short Account of Experimental Researches on the Diffusion of Gases through each other, and their Separation by mechanical means. In: Quarterly Journal of Science, Literature and Art. 27, 1829, pp. 74-83.
- ↑ Thomas Graham: On the Law of the Diffusion of Gases In: Philosophical Magazine. 2, 1833, pp. 175-190.
- ^ A b Thomas Graham: The Bakerian Lecture - On the Diffusion of Liquids In: Philosophical Transactions of the Royal Society of London- 140, 1850, pp. 1-46.
- ↑ Adolf Fick: About Diffusion In: Poggendorff's Annalen der Physik. 94, 1855, pp. 59-86 ( doi: 10.1002 / andp.18551700105 ).
- ↑ a b Albert Einstein: About the motion of particles suspended in liquids at rest, required by the molecular kinetic theory of heat . In: Annals of Physics . 322, No. 8, May 11, 1905, pp. 549-560. Retrieved June 22, 2016.
- ↑ R. Neufeld, D. Stalke: Accurate Molecular Weight Determination of Small Molecules via DOSY NMR by Using External Calibration Curves with Normalized Diffusion Coefficients . In: Chem. Sci. No. 6 , 2015, p. 3354-3364 , doi : 10.1039 / C5SC00670H .
- ↑ Gerd Wedler: Textbook of Physical Chemistry. Verlag Chemie, Weinheim, 1982, ISBN 3-527-25880-9 , p. 95.
- ↑ WA Kreiner: Entropy - what is it? An overview. doi: 10.18725 / OPARU-2609
- ^ HS Carslaw, JC Jaeger: Conduction of heat in solids . 2nd ed. Oxford University Press, London, 1959. ISBN 0-19-853368-3 , p. 28.
- ↑ Yuan-Hui Li and Sandra Gregory: Diffusion of ions in sea water and in deep-sea sediments . Geochimica et Cosmochimica Acta, 38, 1974, pp. 703-714.
- ^ H. Weingärtner, M. Holz: NMR Studies of self-diffusion in liquids. In: Annu. Rep. Prog. Chem., Sect. C. 98, 2002, pp. 121-155.
- ↑ M. Holz, SR Heil, A. Sacco: Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG Measurements. In: Phys. Chem. Chem. Phys. 2, 2000, pp. 4740-4742.
- ↑ E. Bruce Watson, Ethan F. Baxter: Diffusion in solid-Earth systems . In: Earth and Planetary Science Letters. 253, 2007, pp. 307-327.
- ^ M. Weiss, M. Elsner, F. Kartberg, T. Nilsson: Anomalous Subdiffusion Is a Measure for Cytoplasmic Crowding in Living Cells . In: Biophysical Journal . 87, No. 5, 2004, pp. 3518-3524. doi : 10.1529 / biophysj.104.044263 . PMC 1304817 (free full text).





























![{\ displaystyle [J]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50de4527394eeac6ace20edb789515c595c2c73a)
![{\ displaystyle [\ partial c / \ partial x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0b90485811ae81287050bb8eb1634023b05290f)
![{\ displaystyle [D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c4bcb25d77a0de74082c849178200b8cf1340b4)



















