Nuclear magnetic resonance spectroscopy
The nuclear magnetic resonance spectroscopy ( NMR spectroscopy of English nuclear magnetic resonance ) is a spectroscopic method for the investigation of the electronic environment of individual atoms and interactions with neighboring atoms. This enables the structure and dynamics of molecules as well as concentration determinations to be determined.
The method is based on nuclear magnetic resonance , a resonant interaction between the magnetic moment of atomic nuclei in the sample, which is located in a strong static magnetic field, and a high-frequency alternating magnetic field. Only those isotopes are accessible to spectroscopy which in the ground state have a nuclear spin different from zero and thus have a magnetic moment, for example 1 H; 2 D ; 6 Li; 10 B; 11 B; 13 C; 15 N; 17 O; 19 F; 31 P and 43 Approx.
history
For the history of nuclear magnetic resonance spectroscopy see history and development of nuclear magnetic resonance .
Felix Bloch and Edward Mills Purcell first demonstrated nuclear magnetic resonance signals in 1946, for which they received the Nobel Prize in 1952. In their Nobel Prize lecture they showed the first spectra with the detection of the chemical shift (using the example of ethanol), with which the actual nuclear magnetic resonance spectroscopy began. It developed into an important method in chemical structure elucidation. Initially the continuous wave (CW) method was mainly used, in which the resonances were excited one after the other by varying the frequency or the field. In 1947 Russell Varian and Felix Bloch filed a patent for the first nuclear magnetic resonance spectrometer. The first commercial nuclear magnetic resonance spectrometer was built by Varian Associates in Palo Alto in 1952 . Around 1955 the Japanese company JEOL also built NMR spectrometers. The American biophysicist Mildred Cohn used nuclear magnetic resonance spectroscopy in the early 1960s to elucidate metabolic processes at the molecular level.
Since the CW technology was characterized by a poor signal-to-noise ratio , Richard R. Ernst ( Nobel Prize for Chemistry 1991) developed a pulse Fourier transform NMR spectrometer (FT-NMR) at the Varian company from the mid-1960s ), which enabled the spectra to be recorded much faster. With the same measurement time, this means a significant increase in sensitivity and thus in the signal-to-noise ratio compared to the CW spectrometers. Hahn and Torrey had already examined the first pulse methods in 1949 and 1950. The first commercial nuclear magnetic resonance pulse spectrometers were built in the mid-1960s by the German company Bruker (founded by Günther Laukien , one of the NMR pioneers in Germany) in Karlsruhe by a group led by Bertold Knüttel and Manfred Holz . The introduction of broadband decoupling and multi-pulse methods followed. Based on an idea by Jean Jeener , multi-pulse experiments with a systematically varied waiting time between two pulses were developed from the beginning of the 1970s, which after Fourier transformation over two time ranges led to two-dimensional spectra .
Kurt Wüthrich and others developed this 2D and multi-dimensional NMR into an important analysis technique in biochemistry, in particular for the structural analysis of biopolymers such as proteins . Wüthrich received the Nobel Prize in Chemistry in 2002 for this work. In contrast to X-ray structure analysis, nuclear magnetic resonance spectroscopy provides structures of molecules in solution. Of particular importance is the possibility of obtaining detailed information about the molecular dynamics with the help of relaxation parameters.
Physical background
Quantum mechanical fundamentals
Particles and atomic nuclei that have a nuclear spin have, as rotating charge carriers, a magnetic moment that is often referred to as. The magnetic moment of atomic nuclei cannot adopt any arbitrary orientation in an external magnetic field, but only certain orientations described by quantum mechanics . The number of possible orientations is determined by the nuclear spin quantum number (see: Multiplicity ). Orientations exist for each nuclear spin quantum number and a magnetic nuclear spin quantum number is assigned to each orientation .
Examples:
- Hydrogen core with nuclear spin : two orientations with and
- Deuterium core with nuclear spin : three orientations with , and
Without an external magnetic field, the states marked with are energetically the same (see degeneration (quantum mechanics) ). In the presence of an external magnetic field, energy differences arise ( Zeeman effect ). Nuclear resonance phenomena are based on the excitation of nuclear spin transitions between such states. The energy required for this is proportional to the strength of the external magnetic field and the gyromagnetic ratio of the atomic nucleus under consideration:
This energy is brought in through the radiation of resonant electromagnetic waves . The resonance frequency is called the Larmor frequency in NMR spectroscopy and is in the radio wave range. Common NMR spectrometers work at proton resonance frequencies between 300 and 1000 MHz, which requires field strengths between 7 and 24 Tesla.
If all 1 H or 13 C atoms had exactly the same Larmor frequency, the NMR method would be of little interest for structure elucidation. In fact, the resonance frequencies depend on the individual, atomically active magnetic fields. These local magnetic fields can differ in their strength from the main magnetic field, for example due to the influence of the electronic environment of an atomic nucleus or due to magnetic interaction between neighboring atomic nuclei. Because of these properties, nuclear magnetic resonance spectroscopy is used to determine the structure of molecules.
Measurement method of nuclear magnetic resonance spectroscopy
For the measurement, the sample is placed in a homogeneous magnetic field, the so-called main magnetic field. The sample is surrounded by an induction coil, which generates a high-frequency alternating electromagnetic field perpendicular to the main magnetic field. Then the strength of the main magnetic field is varied until the case of resonance occurs (continuous wave method, obsolete). Alternatively, the magnetic field strength can be kept constant and the frequency of the radiated alternating field varied (continuous field method, out of date). When the case of resonance occurs, i.e. the sample absorbs energy from the alternating field, the current strength changes which is required to build up the alternating field. This is measurable.
Modern measuring methods no longer radiate continuous alternating fields into the sample, but rather radio wave pulses. A short radio wave pulse stimulates a frequency band whose frequency width is inversely proportional to the pulse duration via the Fourier relationship . As a result, all transitions in the sample that fall in this frequency band are excited simultaneously. With the correct choice of pulse duration and pulse power , the magnetization of the excited nuclear spins can be brought into the transverse plane perpendicular to the main magnetic field. After the end of the pulse, this transverse magnetization oscillates for a short time perpendicular to the main magnetic field. Each nuclear spin oscillates with its individual Larmor frequency. This sum of these oscillations is detected as an electric current via electromagnetic induction with the same induction coil that was used to send the excitation pulse. The received signal is digitized and recorded. With the help of the fast Fourier transformation it is possible to extract the individual Larmor frequencies from the sum of the oscillations in order to obtain an NMR spectrum. That is why modern NMR methods are called PFT-NMR for Pulsed Fourier Transform NMR Spectroscopy. For this process, the main magnetic field remains static, usually it is generated with the help of superconducting electromagnets that are cooled with liquid helium and nitrogen.
A special method is NMR- CIDNP spectroscopy , in which the sample is irradiated with light or heated to generate radicals.
Relaxation
There are three relaxation processes in PFT-NMR, which on the one hand limit the performance of PFT-NMR, but on the other hand can provide unique information on molecular dynamics and material inhomogeneities. The relaxation is the process of the return of the nuclear spins from the excited state to thermal equilibrium, releasing the energy absorbed during the excitation as heat. If the complete relaxation is not waited for between two NMR experiments ( scans ) , only a certain, lower magnetization and thus signal intensity is available for each subsequent one. If a short repetition time is desired, the excitation angle must be reduced (to the so-called Ernst angle ) in order to still obtain the strongest possible signal. The relaxation is the dephasing of the transverse magnetization due to entropic effects, which is related to the magnetic dipole-dipole interaction of neighboring atomic nuclei. No energy is given off here, since the spins remain in the excited state, but the transverse magnetization diverges from a vector first to a fan and finally to a circular area, so that no more NMR signal is induced in the detection coil. If there are additional magnetic field inhomogeneities in the sample, be it due to imperfections of the main magnetic field or due to differences in susceptibility within the sample, the accelerated relaxation is observed instead of the relaxation .
The relaxation or relaxation limits the lifetime of the NMR signal directly after excitation. The NMR signal is therefore measured as a damped oscillation, as FID ( free induction decay ). In practice, the relaxation time is measured using the spin-echo method.
The relaxation limits how quickly NMR experiments can be carried out one after the other. The relaxation and relaxation depend heavily on the density and viscosity / rigidity of the sample.
Sensitivity of NMR Spectroscopy
An inherent problem with NMR spectroscopy is its comparatively low sensitivity (poor signal-to-noise ratio ). This is due to the fact that the energy differences between the states are small and the population differences between the states in thermal equilibrium are very small ( Boltzmann distribution ).
The occupation ratio of the two energy states involved can be expressed by their energy difference in relation to the thermal energy at a given temperature T:
This is the Boltzmann constant . The energy difference corresponds to the energy of an energy quantum ( ) that transports a particle from the more favorable to the less favorable state (basic equation of spectroscopy ). At a resonance frequency of 600 MHz and a temperature of 0 ° C (273 K) the result is a value of approximately e −0.0001 , i.e. very close to one. Therefore, in thermal equilibrium, there are almost as many nuclei in the excited state as in the ground state. For comparison: Visible light has frequencies that are around a million times higher. As a result, transitions that are excited by visible light have population differences of about e −100 , i.e. they are completely in the ground state, which makes spectroscopy in the visible range much more sensitive.
The sensitivity is therefore essentially dependent on four factors:
- Temperature (dependence ),
- Difference in energy states (proportional to magnetic field strength and isotope-specific gyromagnetic ratio ),
- Frequency of the isotope,
- Spin quantum number of the isotope under consideration.
| NMR properties of hydrogen | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
The factors and the spin quantum number can be expressed by the relative sensitivity . Here, 1 H used as reference. Thus, for an isotope with spin quantum number and the gyromagnetic ratio at the same temperature, the same magnetic field and the same isotope frequency, the relative sensitivity results :
If this value is multiplied by the natural abundance of the isotope, the absolute sensitivity is obtained . The relative sensitivity to 13 C is given as a reference less often.
Various measures are taken to increase sensitivity:
- Measurement of the most sensitive nuclides possible (especially 1 H),
- Accumulation of magnetic nuclides (such as 13 C or 15 N) whose natural abundance is low (e.g. in proteins),
- Signal accumulation through multiple measurements of a sample and addition of all spectra,
- Increasing the magnetic field strength through the use of stronger ( superconducting ) magnets,
- Lowering the temperature of the sample,
- Reduction of electronic noise by cooling the receiver (cryoelectronics),
- Use of hyperpolarization methods to artificially increase the population differences
- Exploitation of the core Overhauser effect (NOE),
- Transfer of the magnetization of sensitive nuclei ( 1 H) to less sensitive ones ( 13 C) (cross polarization CP).
The lowering of the temperature and the increasing of the magnetic field strength change the thermal population equilibrium of the -states, so that more nuclear spin transitions can be excited. With the help of hyperpolarization, an occupation imbalance can be created that deviates greatly from the thermal equilibrium and in which the energetically most favorable state is almost completely occupied.
Low -noise electronics are used to optimize signal detection . The use of electrical oscillating circuits limits the detection to a narrow frequency band in the range of the expected Larmor frequency, i.e. H. the detection of interfering signals and noise from other frequency ranges is suppressed.
Signal accumulation is used to improve the signal-to-noise ratio . An NMR measurement is carried out in an identical manner and the signals measured from the individual measurements are added together. This accumulation increases the NMR signal strength by a factor , while statistical noise increases by a factor of only . Since the complete relaxation of the spins should take place between NMR experiments and the relaxation of organic substances can take a few tens of seconds, the signal accumulation can lead to a considerable increase in the measurement time.
For typical measurements, approx. 10 nmol to 1 µmol of substance are required depending on the experiment and measuring time (typical sample amount: 1 mL of a solution with a concentration of 10 µmol / L to 1 mmol / L).
Resolving power
The achievable resolution of a pulse spectrometer is inversely proportional to the length of the FID signal. In addition to the transverse relaxation ( ) of the sample, it is determined by the inhomogeneity of the field in the sample. The compensation of magnetic field inhomogeneities takes place via what is known as shimming . For this purpose, weak magnetic fields are generated in the spectrometer with the help of electrical currents in addition to the main magnetic field, with which local inhomogeneities can be partially compensated. The increased homogeneity of the resulting overall magnetic field reduces relaxation, which makes the NMR signal longer-lived.
To get the highest resolution in the spectrum, i. H. narrow (sharp) NMR lines and the ability to distinguish closely adjacent lines, another technique must be used, namely the rapid rotation (in English. spinning ) of the measuring cell around its longitudinal axis with the help of a small air turbine. As a result of this macroscopic movement of the sample, the nuclei in the sample experience a time average value of the external field over the sample volume. The magnetic field inhomogeneities remaining after shimming are thus averaged out. In this way one finally achieves a frequency resolution in the NMR of approx. 0.1 Hz, which means that extremely small energy differences can be distinguished, which can then provide a wealth of details from high-resolution NMR spectra.
application areas
NMR spectra can be recorded most easily for molecules that are in solution and do not interact with paramagnetic substances. NMR spectroscopy of paramagnetic substances and solids is also possible, but the interpretation of the spectra and the preparation of the samples for the measurement are much more complex in both cases. With regard to the NMR on solids cf. also magic angle spinning .
The high-resolution nuclear magnetic resonance spectroscopy in solution is used today on a large scale for the following tasks:
- for the non-destructive detection of the constituents of a sample,
- for determining molecular structures (from small molecules to proteins and nucleic acid fragments),
- to study interactions between molecules.
In addition to spectroscopic investigations, the determination of nuclear spin relaxation times provides information about the structure and dynamics of materials. In liquids e.g. B., whose microstructure and dynamics are difficult to research with conventional methods, distances between molecular neighbors and molecular reorientation times, which are typically in the picosecond to nanosecond range, can be determined by means of relaxation time measurements.
Different magnetic resonance relaxation times in different biological tissues form the basis for the magnetic resonance tomography (magnetic resonance tomography) used in medicine as an imaging diagnostic method . One application of nuclear magnetic resonance, which has become extremely important in neurosciences such as neurology and neuropsychology , is functional magnetic resonance imaging . The NMR spectroscopic measurement of metabolite concentrations in vivo is known as magnetic resonance spectroscopy . Magnetic resonance tomography methods are generally used, in addition to medical diagnostics, also increasingly in engineering and geosciences.
Another important area of application is the investigation of translational molecular dynamics, i.e. of diffusion and flow movements of molecules or molecular aggregates in liquids and solids by means of field gradient NMR . With so - called diffusion-ordered-spectroscopy (DOSY), the translational mobility of the individual components identified by NMR spectroscopy can be measured in mixtures. In addition, the molecular weight of molecules in dissolved form can be determined with the aid of the DOSY-NMR experiment .
Methods for structure elucidation in organic chemistry
Chemical shift and integration of signals

The resonance frequencies are not given as absolute values, but as a chemical shift compared to a reference substance, the so-called standard. The chemical shift is defined as
- ,
making it independent of the field strength of the magnet being used. Since the chemical shift values are very small, they are given in ppm . The resonance frequency of the respective nuclei in tetramethylsilane (TMS) is used as the standard for 1 H and 13 C spectra of organic solutions . Whereas in the past a few milligrams of TMS were added to each sample, nowadays one usually refers to the known chemical shift of the residual protons of the deuterated solvent.
The chemical shift of hydrogen nuclei in organic molecules is influenced by the type of functional groups. Depending on the structure of the molecule, the chemical shifts of the same functional groups differ slightly from one another, so that the NMR spectrum is characteristic of a substance. In addition, they are influenced by neighboring molecules in the sample, so that different relative and absolute resonance frequencies of the protons of a sample occur in different solvents or in the pure substance. With strong interactions between substance and solvent, differences of several ppm occur. The chemical shift can be estimated with the help of the Shoolery rule .
In simple 1 H spectroscopy, the relative number of hydrogen atoms on which a certain signal is based is proportional to the area (the integral ) of the signal in question.
By evaluating this integral it can be determined, for example, how many hydrogen atoms in a molecule are on methyl groups, on aromatics, on carboxy groups, on double bonds, etc. This knowledge is extremely important for organic chemistry when determining structures. The following table provides an overview of the assignment of certain functional groups (atomic groups, substance groups) to values of the chemical shift.
| Hydrogen atoms | typical chemical shifts [ppm] |
|---|---|
| H 3 C– | 0.9 |
| H 3 C vinyl R 3 | 1.6 |
| H 3 C-Ar | 2.3 |
| H 3 C-CO-R | 2.2 |
| H 3 C-OR | 3.3 |
| R 2 C-CH 2 -CR 2 | 1.4 |
| -C-CH 2 -Cl | 3.6 |
| Ar-H | 6.8 to 7.5 (up to 8.5 for heteroaromatics) |
| R-CHO | 9 to 10 |
| R-COOH | 9 to 13 |
| RAW | 0.5 to 4.5 |
Scalar coupling
Spin states are split up into energetically different levels by further nuclei that are in their neighborhood and have non-zero spins. The number of these levels depends on the number of possible different orientations of the individual spins. This scalar coupling is mediated by the spins of the electron pairs that form the bond between the particles; their effect can usually be determined from up to four bonds. The distance between the lines is independent of the applied field and is therefore given as an absolute frequency difference (in Hertz ). With nuclei that are chemically and spin-symmetrically the same ( magnetically equivalent ), the coupling is not visible.
From the observed coupling pattern, the spectroscopist can deduce the neighborhood relationships of the individual nuclei and thus in many cases the complete structure of a connection.
Sometimes it can be helpful to suppress certain or all couplings for the structure elucidation. For this purpose, a radio signal with the frequency of a core or a whole group of cores (broadband decoupling) is emitted; the rest of the spectrum then behaves as if the corresponding core were not present. 13 C spectra are 1 H-decoupled by default , as they would otherwise often be uninterpretable due to the overlapping of the coupling patterns of the individual nuclei. In addition, the lack of splitting improves the low sensitivity of the method .
In solid or highly viscous samples, the direction-dependent part of the scalar coupling and the dipolar coupling are no longer averaged to zero. Such samples show large, field-independent splits or line broadening of several kilohertz for 1 H spectra.
Organic NMR Spectrum Set
The organic NMR spectrum set comprises six - in the case of an existing and easily measurable hetero atom (e.g. 31 P or 19 F) - seven NMR experiments which (especially in connection with data from mass spectrometry , IR spectroscopy and UV / VIS -Spectroscopy ) are particularly helpful for elucidating the structure of an organic compound and are therefore usually carried out first to elucidate a structure. These are, in descending order of importance:
- 1 H-NMR
- 1 H-COZY ( correlation spectroscopy )
- 13 C-DEPT or 13 C- APT -NMR, ( distortionless enhancement by polarization transfer ) or ( attached proton test )
- for example 31 P or 19 F-NMR (heteronuclear spectra, if a heteroatom is present)
- 1 H- 13 C-HSQC or 1 H- 13 C-HMQC, ( heteronuclear single quantum coherence ) or ( heteronuclear multiple quantum coherence )
- 1 H- 13 C-HMBC ( heteronuclear multiple bond correlation )
- 1 H-NOESY ( nuclear Overhauser effect spectroscopy )
Working principle
The core susceptibilities are much lower than the diamagnetic and paramagnetic susceptibilities (factor: 10 4 ). With dia- and paramagnetism, the electrons of the atom are responsible for the susceptibility. In the case of nuclei, the susceptibility can be determined using the Langevin-Debye formula.
In the past, NMR resonances were determined with a bridge circuit in resonant circuits . Bloch and co-workers used two identical oscillating circuits, i. H. two coils and two capacitors to make a balance with a bridge circuit; a coil as a transmitter one as a receiver. It is possible to make a bridge circuit with just one coil. This method was used by Purcell.
Before the sample measurement, the bridge is compared with the frequency to be measured. With equations from physics, one can calculate the phase shift between current and voltage, the impedance and the currentless conditions of a bridge for a resonant circuit and a bridge circuit.
A substance tube is now inserted into the coil. A magnetic field (with a permanent magnet or electromagnet) is then created horizontally to the coil axis. At a very specific frequency and a specific magnetic field strength and only if a substance sample is present (with corresponding atomic nuclei), the resonant circuit is detuned. In the oscilloscope or with a recorder this mood is visible.
The determination of the spatial magnetization by the applied magnetic field was very important. Bloch carried out calculations for all spatial directions and was able to derive the vibration-dependent susceptibilities for the spatial directions (Bloch equations). However, the question of the relaxation time remained unresolved, that is, the length of time until the excited nuclear spin falls back to the basic level. Using paramagnetic salts, the relaxation time of pure hydrogen protons could then be calculated to be about three seconds.
Hydrogen nuclei could be detected at very low frequencies (a few kilohertz) and a very weak magnetic field due to resonant circuit detuning. The method becomes interesting for the structure elucidation of complex molecules, however, only at high frequencies (from 60 MHz) and stronger magnetic fields (1.4 Tesla), since then the chemical shifts of different hydrogen atoms of complicated compounds differ more clearly. However, if you want to see not just a single signal on the oscilloscope, but several different hydrogen atom nuclei (or other nuclei), an entire frequency band must be radiated.
In the past - until the 1970s - NMR spectrometers used the continuous wave method (CW) to scan the spectrum of a complex compound.
Today the pulse Fourier transform (PFT) is common. A high-frequency pulse is emitted here. This impulse contains a whole band of vibrations.
The above-mentioned dependence of the energy levels of the nuclear spins on the molecular structure is primarily due to the interaction of the electronic structure of the molecules with the external magnetic field: This creates an induction current in the electron shell , which in turn generates a magnetic field that is opposite to the external one. This weakens the magnetic field at the atomic nucleus, so the frequency of the radiation necessary for the transition is lower than in the case of a naked atomic nucleus. The difference is called the chemical shift and is usually given in relation to the frequency required for the bare atomic nucleus. Chemical shifts are typically in the range of 0-5000 ppm.
The magnetic field at the atomic nucleus is influenced by the alignment of other magnetic moments in the immediate vicinity. For example, if there is a core with two alignment options nearby, it can either strengthen or weaken the field. This leads to a splitting of the signal, one speaks of a coupling. Because the chemical shift essentially depends on the electron density at the atomic nucleus, one can expect similar displacements for atomic nuclei in chemically similar environments. The coupling also provides information about the proximity relationships between different nuclei in a molecule. Taken together, both provide essential information about the structure of the entire molecule.
Nuclei with odd proton - and / or neutron -Number have a nuclear spin I . This can assume integer and half-integer values (e.g. 1/2, 1, 3/2, ..., 9/2): with the so-called uu kernels, I = n (i.e. only integer: 1, 2, 3 , ...) while for gu and ug nuclei I = (2 n +1) / 2 ( i.e. half-integer : 1/2, 3/2, 5/2, ...), for isotopes with an even number of protons and neutrons ( so-called gg nuclei) I = 0. Nuclear spins that differ from zero are associated with a magnetic dipole moment . The size of this dipole moment is described by the gyromagnetic ratio of the relevant isotope. In an external, static magnetic field, nuclear magnetic moments align themselves according to the rules of quantum mechanics . An atomic nucleus with I = ½ has the shape of a sphere, nuclei with I> ½ have an ellipsoidal shape and therefore also have an electric quadrupole moment "eQ", which can interact with electric field gradients (see also nuclear quadrupole resonance spectroscopy ). This additional, strong electrical interaction possibility leads to broad NMR resonance lines, which are more complicated to interpret than the narrow resonance lines of the spin ½ nuclei, which are structured by easily resolvable couplings.
The isotopes most used for chemical structure elucidation are therefore nuclei with spin ½. These include the nuclides 1 H, 13 C, 15 N, 19 F, 29 Si and 31 P. Spin-½ nuclei can only assume two discrete states, namely either parallel or antiparallel to the external magnetic field. Intermediate positions are forbidden in quantum mechanics. The two possible arrangements correspond to two different energy states.
The energy difference between these two states is proportional to the strength of the magnetic field at the nucleus. The proportionality factor is the gyromagnetic ratio of the isotope in question. Transitions between the two orientations of the nuclear moments can be triggered by the radiation of resonant alternating magnetic fields . The resonance frequency is proportional to the energy split between the two nuclear spins and is called the Larmor frequency .
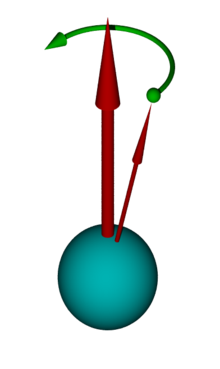
This can be illustrated by the diagram opposite. Here one imagines a coordinate system with the external magnetic field along the z-axis. An atomic nucleus with a spin of ½ aligns itself with a spin vector either parallel or antiparallel to the external field. If you now include the vectors of several atoms in this coordinate system, two cones are created, one each for parallel and antiparallel. Due to the energy difference between the parallel and the antiparallel orientation of the nuclear magnetic moments, there is a population difference between the two orientations in thermal equilibrium. This follows the Boltzmann distribution in a high-temperature approximation and causes excess magnetization in the positive direction along the z-axis.
The NMR signal is generated by exposing the sample to be examined to a radio frequency pulse in a magnetic field. The spins of the individual atoms are influenced by the magnetic field of the pulse, so that the overall vector, which results from the spin cones shown, is tilted. It is now no longer parallel to the z-axis, but is deflected by an angle that is proportional to the duration and intensity of the radio frequency pulse. Pulse lengths of around 1–10 µs are typical. A maximum transverse magnetization perpendicular to the z-axis is achieved with a deflection angle of 90 °.
This transverse magnetization behaves like a magnetic top and precesses in the plane perpendicular to the static magnetic field. This precession movement is noticeable as a very weak alternating magnetic field, which is measured using a suitable amplifier. After the end of the resonant irradiation, two processes, so-called relaxation processes, occur , through which the transverse magnetization decreases again. The NMR signal is thus measured as free induction decay (FID) after the radio frequency pulse has ended . The time constant of this free induction decay depends on the transverse relaxation time and on the homogeneity of the magnetic field. For fluids that move easily in homogeneous magnetic fields, it can be in the range of several seconds. The FID is modulated by the frequency differences due to chemical shift and coupling. The distribution of the various frequencies can be calculated from the FID using a Fourier transformation . This is then the NMR spectrum. In many cases, the NMR spectrum provides a clear “fingerprint” of the respective molecule. Together with information from other measurements such as B. mass spectrometry , the chemical structure of an unknown substance can be determined from the spectra.
Commercial NMR spectrometers for chemical structure elucidation usually work at magnetic flux densities between 7 and 21 Tesla . For 1 H the resonance frequencies (Larmor frequencies) then correspond to between 300 and 900 MHz. Since 1 H is the most important NMR nucleus, the field strength of spectrometers is usually expressed in terms of its Larmor frequency. At 1 H the splitting of the spectra is approx. 10 ppm due to different chemical shifts. This corresponds to a maximum bandwidth of approx. 3 kHz at an NMR frequency of 300 MHz. The frequency bandwidth of the NMR spectra as a result of the chemical shift increases proportionally to the magnetic field. The chemical shift itself is defined as the ratio of the difference between the resonance frequency of the nucleus in a certain chemical environment and the resonance frequency in a reference compound to the resonance frequency itself. This allows a simple comparison between NMR spectra measured in different fields. Tetramethylsilane (TMS) is used as the reference substance for hydrogen and carbon . The range of chemical shifts for carbon and many other nuclei is much broader than for hydrogen and can be several hundred ppm. With some very heavy cores such as B. 207 Pb chemical shifts in the range of percent are observed.
Pulse Fourier Transform NMR
Nowadays all modern NMR spectrometers work with the pulse technology. This involves sending a single radio frequency pulse (RF pulse) or a sequence of RF pulses to a sample that is in a strong magnetic field . After the pulse in the receiving electronics has decayed (dead time), the magnetization ( free induction decay , FID), i.e. That is, their return to the equilibrium state is detected via the voltage induced thereby in the receiving coil as a function of time. This time signal is transformed into the frequency spectrum (signal intensity as a function of frequency) in the computer by Fourier transformation.
This measurement technology has almost completely replaced the previously used CW ( continuous wave ) method (see above).
Experimental sizes
- The chemical shift of a resonance depends on the local magnetic field at the nucleus, which in turn depends on the chemical environment of the nucleus in question.
- The intensity of a resonance is usually proportional to the number of nuclei that cause it, as long as the differences in population are not changed by strong coupling or differences in susceptibility.
- With the relaxation times of excited states, a distinction is made between longitudinal relaxation time ( spin-lattice relaxation ) and transverse relaxation time ( spin-spin relaxation ). Longitudinal relaxation times determine the setting of the equilibrium magnetization. The transverse relaxation times determine the line width of the resonance lines. Relaxation effects provide information about existing interactions and molecular movements.
- Spatially adjacent nuclei interact with one another via magnetic dipole-dipole interaction (dipolar coupling). This interaction disappears in isotropic solutions on average over time.
- Nuclei can interact indirectly with one another via chemical bonds. This scalar coupling is responsible for the splitting of the signals into multiplets and is an essential basis for the molecular structure determination with NMR. The distance between two neighboring lines of a multiplet is called the coupling constant, which is measured in Hertz.
One-dimensional NMR spectroscopy
One-dimensional NMR spectroscopy is the most frequently used structure elucidation method in chemistry. With it, the chemical shift of an atom is measured by a reference substance. 1 H and 13 C are the nuclei that are most frequently measured in organic chemistry, but 15 N, 31 P, 19 F and many other NMR-active isotopes can also be spectroscoped.
The appearance of the spectra depends crucially on the type of recording. 1 H spectra are usually not recorded with broadband decoupling. This means that all hydrogen atoms have the option of coupling their spin with other nuclei, the so-called spin-spin coupling. With the characteristic chemical shift of an atom there is a splitting of the signal characteristic of its environment, from which information about the molecular structure can be derived.
13 C, 15 N, 31 P, 19 F and other nuclei are often recorded 1 H broadband decoupled, so that the signals are not split up due to the coupling to 1 H nuclei.
Scalar coupling
The nucleus of an atom can interact with a neighboring nucleus. This can happen either directly (through space) or indirectly (via the binding electrons between the nuclei). In the case of a liquid sample, the direct (dipolar) interaction is averaged out through the rapid movement of the nuclei in space. The scalar coupling is retained, which is mediated by the fact that the spins of the binding electrons (always paired (↓ ↑)) interact differently with the nuclear spins on both sides of the bond.
If a nucleus has the state α (↑), the (↑) -electron of the bond is repelled by it, so it tends to stay at the other nucleus. Further bonds emanating from there are also (to a lesser extent) spin-polarized. If another nucleus is reached, there is an energy difference between its state α and β due to its interaction with the electrons of the bond. Such couplings are usually over max. three to four bonds detectable, in conjugated π systems, for example, but also further.
The NMR signal of the first nucleus is split into a doublet (for , otherwise lines), and that of the second nucleus also, by the same amount, because the energy difference (so-called coupling constant) between αα (= ββ) and αβ (= βα) must be the same. The proximity of the two atoms in the molecule is then demonstrated by the equally strong splitting. If a core couples to other others, each of its lines is split up again accordingly.
If a nucleus couples to two (or generally ) similar neighboring nuclei (which from the point of view of the original nucleus have the same chemical environment and spin symmetry), a triplet is obtained because the middle lines of the "doublet from the doublet" (or quartet, quintet etc., i.e. lines or lines for nuclei with ) coincide. The relative intensities of the lines result (for - nuclei) from the -th line of Pascal's triangle , i.e. 1: 2: 1 or 1: 3: 3: 1. Are the coupling cores not of the same kind , i.e. H. if their coupling constants are different, the middle lines do not coincide. B. a doublet from the triplet or the like.
Sample spectra
Propane (H 3 C – CH 2 –CH 3 ) serves as a simple example : The CH 2 group in propane has two adjacent methyl groups (–CH 3 ). This corresponds to six neighboring, equivalent H atoms. The signal is split up into a septet. The methyl protons are split up by the two methylene protons to form a triplet, the 4 J coupling to the three other methyl protons is invisible because they are magnetically equivalent, and no 2 J coupling can be observed within the methyl groups .
Are several different z. If, for example, methyl groups are present, their multiplets often overlap, making them quickly unevaluable. In order to be able to resolve such cases better, multidimensional NMR techniques such as COZY are often used . Since the splitting is not field-dependent, but the distance between the signals of chemically different protons is, overlays can be resolved by applying a higher field.
Explanations on the spectrum of ethanol :
The OH group only shows a singlet if the ethanol in the sample contains more than 3% water. The alcoholic hydrogen atom is slightly acidic and is therefore constantly exchanged for hydrogen atoms from other hydroxyl groups or from the solvent. This means that no permanent spin-spin coupling effects occur between the OH group and the neighboring methylene group. At very low temperatures or in absolutely anhydrous alcohol, this exchange is slowed down enough to make the expected vicinal coupling ( ) visible.
Two-dimensional NMR spectroscopy
In two-dimensional nuclear magnetic resonance spectroscopy (2D-NMR), the intensities are recorded as a function of two frequency axes. So it generates three-dimensional diagrams. Two-dimensional NMR spectra provide more information about a molecule than one-dimensional NMR spectra and are therefore particularly useful in determining the structure of a molecule, especially for molecules whose structure is too complex to study with one-dimensional NMR.
Low field NMR
There are relatively inexpensive low-field NMR devices (10 ... 60 MHz) which, equipped with a permanent magnet, do not deliver any resolved spectra, but are incomparably cheaper in terms of operating costs (no helium cooling). Such systems can also be designed to be portable. By analyzing the 1 H relaxation times, the proportions of mixtures of multi-substance systems (suspensions, partially crystalline substances) and, after calibration, also absolute quantities of substances can be quantified, which is particularly interesting in industry . Measurements are usually carried out in bulk instead of in an (expensive) deuterated solvent. Nuclei other than hydrogen are rarely investigated due to their low sensitivity.
Deuterium nuclear magnetic resonance spectroscopy
Deuterium (D, 2 H) is special in that it has a spin . As a result, the line width of the NMR signals is larger than that of 1 H nuclei. The resonance frequencies are well below those of 1 H nuclei (61.4 versus 400 MHz at 9.39 Tesla). Deuterium NMR spectroscopy is approximately 100 times less sensitive than 1 H NMR spectroscopy. In addition, the proportion of deuterium in organic compounds compared to hydrogen is very low (approx. 0.0159%). With modern NMR spectrometers, however, the investigation is not a problem today. The recordings and evaluations are carried out using the Fourier transform method. Interpretation of the spectra is not difficult because the chemical shifts are practically identical to those of 1 H.
With 2 H-NMR spectroscopy, the deuterium distribution in the individual positions in an organic compound and the D / H ratio can be determined position-specifically for so-called SNIF-NMR . The deuterium distribution can be read off directly from the spectra, the D / H ratio can only be determined if a standard with a known D / H ratio is used. This method is important for analytics because it allows a statement to be made about the origin of an organic compound. On the one hand, this is due to the fact that the proportion of deuterium on earth is different and the starting materials, for natural substances essentially also water, therefore have a slight difference in the deuterium content. On the other hand, the kinetic isotope effect is important in the synthetic routes . So z. B. Ethanol in wines from different regions has a different deuterium distribution in the molecule or a different D / H ratio. The same applies to all natural substances and thus many of these substances can now be assigned an origin or type of synthesis, whether natural or synthetic.
In the case of ethanol produced from sugar through fermentation processes, the vegetable origin can be determined via the D / H ratio, i.e. whether the sugar comes from sugar cane, beets, grain, corn, potatoes, grapes or apples. In this way, unauthorized added sugar can be determined. In addition to ethanol, other ingredients in wine such as glycerine , methanol , organic acids and preservatives can also be determined qualitatively and quantitatively from 13 C spectra .
Furthermore, Deuterium NMR is a common method for investigating an orientation anisotropy in high molecular weight organic solids (e.g. fibers).
Metal core nuclear magnetic resonance spectroscopy
In addition to the investigation of organic compounds using 1 H, 13 C and 19 F NMR spectroscopy , metal core NMR spectroscopy is also important. Metal-metal or metal- ligand bonds in complex compounds and organometallic compounds can be examined directly. Proteins with embedded metal ions can also be examined. Short-lived intermediate stages, which cannot or can only be detected with difficulty after the reaction, can be detected in the reaction solutions. No special solvents are required, the measurements can be carried out in the reaction solution. Examples are 6/7 Li, 25 Mg, 27 Al-NMR spectroscopy and measurements on heavy metal nuclei , such as. B. 195 Pt, 205 Tl and 207 Pb.
The investigation of electrically conductive metallic solids requires different experimental conditions than those of metal cores in solutions. The nuclear spin quantum number of some metal nuclei is greater than 1/2 (examples: 6 Li: 1, 7 Li: 3/2, 23 Na: 3/2, 25 Mg: 5/2, 59 Co: 7/2). Such nuclei have an electrical quadrupole moment, they relax via a special relaxation mechanism and therefore often have very broad resonance lines, which affects the sensitivity of the NMR measurements.
Manufacturer
The pioneer was the company Varian Associates in Palo Alto , California. Varian was founded in 1948 and manufactured high resolution liquid spectrometers based on continuous wave sweep methods and electromagnets. Significant products were: R30 (1952), HR40 (1955), HR60 (1958), HR100 (1959). With the success of the A-60 spectrometer (1961), Varian became the global market leader.
The company somber, Täuber & Co. AG , Zurich , developed in the 1960s in close collaboration with the ETH Zurich NMR spectrometer and built the equipment KIS KIS 1 and 2 (1963) in a small series. The company closed in 1965.
The Bruker company was founded in Karlsruhe in 1960 and manufactured high-performance magnets, later also NMR spectrometers. In 1965 Bruker took over the research department of the company Trüb and Täuber and thus founded the company Spectrospin AG , Zurich . This synergy resulted in the high-resolution HFX-90 spectrometer with 90 MHz in 1967, the first fully transistorized NMR spectrometer. In 1972, Spectrospin created the first pure FT spectrometer, the WH 90 system, the ancestor of all modern nuclear magnetic resonance spectrometers. In 2010, Bruker had a global nuclear magnetic resonance spectroscopy market share of around 80%.
See also
literature
- Malcom H. Lewitt: Spin Dynamics. Wiley & Sons, Chichester 2001, ISBN 0-471-48922-0 .
- Manfred Holz, Bertold Knüttel: Pulsed nuclear magnetic resonance: The current state of a physical method with a variety of possible applications . In: Physics Journal . tape 38 , no. December 12 , 1982, pp. 368-374 , doi : 10.1002 / phbl.19820381208 .
- Harald Günther: NMR Spectroscopy. 3. Edition. Thieme, Stuttgart 1992, ISBN 3-13-487503-9 .
- Ullmann's Encyclopedia of Technical Chemistry. Volume 5, 4th edition. Weinheim 1980, ISBN 3-527-20005-3 , p. 382 ff.
- A. Streitwieser Jr., CH Heathcock: Organic Chemistry. Verlag Chemie, Basel 1980, ISBN 3-527-25810-8 , pp. 205-249.
- Dudley H. Williams, Ian Fleming: Spectroscopic methods for structure elucidation, nuclear magnetic resonance spectra. Thieme, Stuttgart 1975, ISBN 3-13-437203-7 , pp. 80-161.
- H. Friebolin: One and two-dimensional NMR spectroscopy. 4th edition. Wiley-VCH, Weinheim 2006, ISBN 3-527-31571-3 .
- Stefan Berger, Siegmar Braun: 200 and More Basic NMR Experiments. A Practical Course. Wiley-VCH, Weinheim 2004, ISBN 3-527-31067-3 .
- James Keeler: Understanding NMR Spectroscopy. 2nd Edition. Wiley & Sons, Chichester 2010, ISBN 978-0-470-74608-0 .
- Timothy DW Claridge: High-Resolution NMR Techniques in Organic Chemistry. 2nd Edition. Elsevier, Oxford 2009, ISBN 978-0-08-054818-0 .
Web links
- TU Dortmund: NMR spectrometer (PDF; 2.1 MB; no longer publicly accessible, requires authentication)
- ETH Zurich directory of databases and reference works with 1 H spectra
- ETH Zurich directory of databases and reference works with 13 C spectra
- Easy to understand Shockwave animation of the NMR principle - University of Florida
- Spectra database (not only for NMR) (English)
- NMR spectra database (English)
- Nuclear Magnetic Resonance - Introduction to Theory. Contains a lot of ads and dead links.
- Basics of NMR by Joseph P. Hornak, Ph. D. (English)
- e-MRI - MRI step-by-step, interactive course on magnetic resonance imaging , from Campus Medica
- 1 H-NMR Prediction - online calculation of 1 H NMR spectra
- 1 H-NMR without formulas - introduction to school lessons
- James Shoolery: A Basic Guide to NMR , 3rd Edition, Stan's Library, Vol.II, 2008, doi: 10.3247 / sl2nmr08.012 (English; PDF; 4.15 MB)
- nmr.ch - Swiss NMR Community (English)
- Exercise collection - NMR problems of various degrees of difficulty with sample solutions as PDF download
Individual evidence
- ↑ Continuous-Wave Nuclear Magnetic Resonance (NMR) Spectroscopy. In: adelaide.edu.au. Department of Chemistry, University of Adelaide, archived from the original on March 25, 2012 ; accessed on February 20, 2016 (English).
- ^ Nicole Kresge, Robert D. Simoni, Robert L. Hill: Succeeding in Science Despite the Odds; Studying Metabolism with NMR by Mildred Cohn . In: Journal of Biological Chemistry . tape 279 , no. 53 , December 31, 2004, p. e12 , PMID 15615732 ( online [accessed August 18, 2010]).
- ^ Nobel lecture by Ernst (PDF; 1.5 MB).
- ^ ER Andrew: Nuclear Magnetic Resonance. Cambridge at the University Press, 1958, p. 62.
- ^ C. Reinhardt, T. Steinhauser: Formation of a scientific-technical community. NMR spectroscopy in the Federal Republic of Germany. In: NTM Journal for the History of Science, Technology and Medicine. 16, 2008, pp. 73-101, doi: 10.1007 / s00048-007-0280-z .
- ^ A. Geiger, M. Holz: Automation and control in high power pulsed NMR . In: Journal of Physics E: Scientific Instruments . tape 13 , no. 7 , January 1980, p. 697 , doi : 10.1088 / 0022-3735 / 13/7/001 .
- ^ Nobel lecture by Wüthrich (PDF; 399 kB).
- ↑ R. Blachnik (Ed.): D'Ans, Lax: Pocket book for chemists and physicists . 4th edition. tape 3 : Elements, inorganic compounds and materials, minerals. Springer-Verlag, Berlin 1998, ISBN 978-3-642-63755-1 , p. 13 , doi : 10.1007 / 978-3-642-58842-6 ( limited preview in Google Book search).
- ^ PT Callaghan: Principles of Nuclear Magnetic Resonance Microscopy. Clarendon Press, Oxford 1991.
- ↑ R. Neufeld, D. Stalke: Accurate Molecular Weight Determination of Small Molecules via DOSY NMR by Using External Calibration Curves with Normalized Diffusion Coefficients . In: Chem. Sci. No. 6 , 2015, p. 3354-3364 , doi : 10.1039 / C5SC00670H .
- ^ D. Li, I. Keresztes, R. Hopson, PG Williard: Characterization of Reactive Intermediates by Multinuclear Diffusion-Ordered NMR Spectroscopy (DOSY) . In: Acc. Chem. Res. No. 42 , 2008, p. 270-280 , doi : 10.1021 / ar800127e .
- ^ Matthias Findeisen, Stefan Berger: 50 and More Essential NMR Experiments - A Detailed Guide . Wiley-VCH, Weinheim, 4th edition, 2014, ISBN 978-3-527-33483-4 .
- ↑ Timothy DW Claridge: High-Resolution NMR Techniques in Organic Chemistry . Elsevier, Amsterdam, 3rd edition, 2016, p. 10, ISBN 978-0-08-099986-9 .
- ^ Gregory A. Manley, David Rovnyak: Observing Proton Exchange in Aqueous Ethanol with a 60 MHz FT-NMR Spectrometer. 2006.
- ↑ Andreas Maus, Christopher Hertlein, Kay Saalwächter: A Robust Proton NMR Method to Investigate Hard / Soft Ratios, Crystallinity, and Component Mobility in Polymers In: Macromolecular Chemistry and Physics. 207, 2006, p. 1150, doi: 10.1002 / macp.200600169 .
- ↑ Hans-Otto Kalinowski: The horror of the Weinpanscher. Quantitative Deuterium NMR Spectroscopy . In: Chemistry in Our Time . tape 22 , no. 5 , October 1988, p. 162-171 , doi : 10.1002 / ciuz.19880220503 .
- ^ Adolf Rapp, Alfred Markowetz: NMR spectroscopy in wine analysis . In: Chemistry in Our Time . tape 27 , no. 3 , July 1993, p. 149–155 , doi : 10.1002 / ciuz.19930270307 .
- ↑ Bernd Wrackmeyer: NMR spectroscopy of metal cores in solution . In: Chemistry in Our Time . tape 28 , no. 6 , December 1994, pp. 309-320 , doi : 10.1002 / ciuz.19940280610 .
- ^ Richard R. Ernst: Zurich contributions to the 50-year development of Bruker . doi : 10.1002 / anie.201005067 (free full text).