Zeeman effect
The Zeeman effect [ ˈzeːmɑn -] is in atomic physics the splitting of spectral lines by a magnetic field. The split occurs due to the different shifts of energy levels of individual states under the influence of an external magnetic field . The effect was first demonstrated in 1896 by Pieter Zeeman . Three years later, Hendrik Antoon Lorentz managed to explain it on the assumption that the light emitted by atoms is generated by moving electrons. In 1902 they both received the Nobel Prize in Physics .
The energy shifts result from the effect of the magnetic field on the magnetic moment of the atomic shell , which is generated by the orbital angular momentum and the spin of the electrons . The effect is also available for nuclear spin , here with splits that are around 1000 times less due to the magnetic moment of the nuclear spins being around a factor of 1000 smaller .
The energy shift due to an electric field is called the Stark effect .
Discovery and Importance
In order to discover possible connections between different forces of nature, in the 19th century a. a. Long searched for the influence of magnetic fields on light (see e.g. Faraday effect ). From the idea of classical physics that light is created as an electromagnetic wave by oscillations of the (whole) atoms, Hendrik Antoon Lorentz theoretically derived a formula in 1892 according to which the spectral lines are split up three times when the radiating atoms are in a magnetic field . In detail, the middle of the three lines should show the undisturbed frequency and the frequency of the other two lines should be shifted up or down by the frequency of the Larmor precession caused by the magnetic field . When observing parallel to the magnetic field, the two shifted lines should also be circularly polarized in opposite directions and the middle line should not appear at all. Zeeman was able to observe all of this for the first time in 1896, albeit with a split many thousand times greater than expected. Subsequent precise measurements of the splitting showed that it still corresponds to Lorentz's formula when it is applied to the case that when light is emitted, it is not the atom with its entire mass that vibrates, but only the much lighter electron . At that time, the electron hypothesis that electrons are part of atoms was only assumed. The Zeeman effect and its successful explanation made this view much more persuasive in physics at the time.
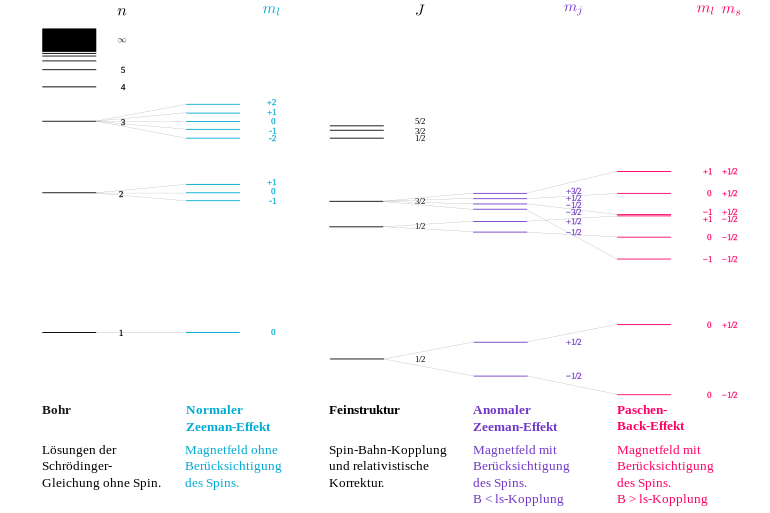
However, Lorentz could only explain a threefold splitting, which was therefore called the normal Zeeman effect . The normal Zeeman effect was contrasted by a larger number of observations in which more than three lines emerged from the splitting. This so-called anomalous Zeeman effect was an inexplicable phenomenon for classical physics and also for Bohr's atomic model, and it was precisely for this reason that further theoretical investigations were initiated. Odd-numbered splits in more than three lines were explained in the Bohr-Sommerfeld atomic model from 1916 onwards by the directional quantization of the orbital angular momentum . In contrast, the even-numbered splits in 1925 led to the discovery of a new type of angular momentum, the electron spin . The size of the splits, which deviates from the normal Zeeman effect, could be parameterized with the Landé factor , which was justified in quantum mechanics from 1925 . In deviation from the original use, the splitting without the involvement of the spin is predominantly referred to today as the normal Zeeman effect, and that with the involvement of the spin as the abnormal Zeeman effect . (For more information, see.)
Normal Zeeman effect
The normal Zeeman effect occurs when the angular momentum of the system under consideration does not contain any part of the particle's spin (i.e. quantum number for the total spin). It could already be explained in the context of classical physics.
Classic explanation
An electron on a circular path with the (circular) frequency forms a circular current and therefore has a magnetic dipole moment in addition to a mechanical angular momentum . Both vectors are parallel, perpendicular to the plane of the orbit and have a fixed size ratio , because the gyromagnetic constant for simple orbital angular momentum depends only on the electrical charge and the mass of the electron (for more details, especially to take into account anomalous gyromagnetic relationships, for example in the case of the electron , see the given keywords).
The potential energy of a magnetic dipole depends on its orientation towards the magnetic field :
Here and is the component of the magnetic moment that is parallel to the field direction. is the magnitude of the field strength.
The torque , which would turn a stationary bar magnet in the direction of the field lines (such as the compass needle pointing north), causes the Larmor precession in the presence of an angular momentum , in which the vector without changing the setting angle, i.e. with a constant component , around the Field direction is swung around. The angular velocity of precession is the Larmor frequency
The previously purely circular movement of the electron thus becomes a rosette orbit . It contains periodic movements of the electron in directions parallel and perpendicular to the magnetic field. Harmonic decomposition shows that the movement parallel to the magnetic field is not influenced and continues with the undisturbed frequency . The movement perpendicular to it contains two opposite circular movements with the sideband frequencies . According to classical physics, every wave generated by the electron receives the same three frequencies. Its other properties are particularly simple if the observation is made in the direction of the magnetic field (longitudinal) or perpendicular to it (transversal). In the longitudinal Zeeman effect, the center frequency does not occur at all because a dipole does not radiate in the direction of oscillation. The two sidebands then show opposite circular polarization . At right angles to the magnetic field, in the transverse Zeeman effect, one sees linearly polarized radiation of all three frequencies, the polarization of the center frequency being in the direction of the magnetic field, that of the sidebands being perpendicular to it. This precise description of the normal Zeeman effect by H. A. Lorentz also corresponds quantitatively to the observation if the gyromagnetic factor is given the correct size according to the formula given above . The atomic mass was originally used in the denominator, so that the split was predicted too small by a factor of several thousand. This fact was an important step towards the realization that electrons play a crucial role in the emission of light.
This classic explanation applies equally to a single electron as to a system of several electrons, e.g. B. for the entire electron shell of the atom (if the total spin is zero). and then denote the entire angular momentum or the entire magnetic moment of the shell (often with capital letters and written), whereby the gyromagnetic factor in particular remains the same, regardless of the other details of the movement of the electrons through each other.
Quantum mechanical explanation
According to quantum mechanics , the electron does not radiate while it is in a stationary state, but rather during the transition between two states, both with a certain energy, whereby the frequency of the emitted wave results exclusively from the difference between the two energies (quantum condition with the angular frequency and the reduced Planck's quantum of action ):
The classical formulas used above for the magnitude of the magnetic dipole moment and its energy in the magnetic field continue to apply unchanged, provided that the magnetic effects associated with the electron spin can be disregarded. This condition is never fulfilled for a single electron, but only in systems with an even number of electrons in states in which the electron spins add up to the total spin . Instead of the orbital angular momentum of the individual electron, the sum of all orbital angular momenta has to be taken, and accordingly the component along the field. In a steady state it can only have discrete values . The magnetic quantum number runs through all integer values between and , whereby the (always integer) orbital angular momentum quantum number is the relevant state. (For details see under directional quantization .)
The energy level of a previously degenerate state splits into energetically equidistant Zeeman levels with energy shifts
relative to the original level. These have a distance from each other
The size is called Bohr's magneton . States with do not split at all (so-called singlet ), states with triple (triplet), etc.
The normal Zeeman effect is obtained e.g. B. at a transition from a state with to a with . The magnetic splitting causes, via the quantum condition, the frequency shifts around or zero observed on the spectral lines . The circular polarization (around the field direction) results from the fact that the z-component of the angular momentum of the electron changes by and the generated photon must have the opposite angular momentum because of the conservation of angular momentum.
The same formulas also apply to all higher orbital angular momenta , with the energy levels also splitting by multiples of due to the factor . The corresponding splitting of the spectral lines by multiples of is not observed, however, because such transitions would require the emission of several photons at the same time due to the constant torque of the photon, which is a strongly suppressed process. Therefore practically only transitions occur. With the Zeeman effect, one generally observes fewer spectral lines than the number of Zeeman levels that arise from the splitting indicates. Because of this common explanation (level shift depending on ), all of these cases are grouped under the single term of the normal Zeeman effect.
Anomalous Zeeman effect
With moderate field strength
In the anomalous Zeeman effect, which is much more common than the normal Zeeman effect, the spectral lines are split into more than three lines, often in an even number (quartet, sextet, etc.). The spin must be used for interpretation. This intrinsic angular momentum of the electron, which can not be explained according to classical physics, is only half as large as the unit of the orbital angular momentum, but it contributes to the magnetic effect with the same strength (1 Bohr magneton ). With the anomalous Zeeman effect, orbital and spin magnetism occur. The magnetic moment associated with the spin is written with the anomalous g-factor of the spin . In the case of the Russell-Saunders coupling , the total angular momentum of the atomic shell is composed of the sum of all orbital angular momenta ( with quantum number ) and the sum of all spin angular momentum ( with quantum number ) of the electron (s ):
The resulting magnetic moment is no longer completely by the quantum number determines the total angular momentum, but depends more on how large the railway and the spin angular momentum quantum numbers and are in it. This flows into Landé's g-factor of the level. The level is split into equidistant Zeeman levels in the (weak) magnetic field . The anomalous Zeeman effect is thus a split into different ones . The normal Zeeman effect is the special case of the anomalous Zeeman effect, in which the following applies because the spin has no influence. The energy shift of the Zeeman level with is
- .
If the initial and final state of the transition that produces the spectral line under consideration are of different sizes, this causes the observed line splitting into more than three lines. In clear terms, the total angular momentum of the envelope precesses in the initial state with a different Larmor frequency than in the final state.
After Landé formula of the g-factor is a level simply from the quantum numbers , and predictable. The prerequisite is that the quantum numbers for the sum of the orbital angular momentum alone and the sum of the spins alone are well defined. For atoms with only one electron outside closed shells (e.g. H, Na and other alkali metals), this is always given by its quantum numbers and . In the case of several electrons outside closed shells, the LS coupling must be present, which is usually the case for the lighter elements. With the help of Landé's formula it was possible to determine the three quantum numbers for a multitude of levels of different atoms, which was a decisive factor in deciphering the structure of the atomic shell (see also term symbol ).
With high field strength
As the magnetic field becomes stronger, the anomalous Zeeman effect shows deviations from the equidistance of the splitting, and some of the individual lines approach one another in such a way that ultimately the picture of the normal Zeeman effect with only three splits results. This is known as the Paschen-Back effect . It is explained by the fact that the applied magnetic field is strong enough to break the originally existing coupling from and to a well-defined total angular momentum with a well-defined quantum number , so that the levels involved become superimpositions of different total angular momenta. To do this, the external magnetic field must be so strong that the level split is far greater than the original energy difference to the next level of the multiplet, which has a different total angular momentum for the same quantum numbers and for orbital angular momentum and spin . Under these conditions, the magnetic moments of spin and orbital angular momentum adjust independently of each other to the magnetic field and, because of their equal size, cause the same level splits. The energy split is:
Because of the value , half- integer values of result in an integral multiple of as in the normal Zeeman effect.
Zeeman effect in nuclei
The anomalous Zeeman effect has also been observed in atomic nuclei. This is remarkable insofar as the nuclear magnetic moments are approx. 10 3 -10 5 times smaller than with the atomic shell (see the factor mass in the formula above), while the frequencies of the typical gamma radiation of nuclei are at least 10 4 times higher than with optical spectral lines. The Zeeman effect, which thus requires at least 10 8 times better spectral resolution, was demonstrated in the 1960s with the help of the Mössbauer effect on the nuclei of 57 Fe, which were exposed to the extremely strong internal magnetic field in magnetized iron .
Square Zeeman Effect
A magnetic field always induces a moment even in closed shells of the atomic shell without a permanent magnetic moment:
with the magnetic polarizability .
This also interacts with the external magnetic field and leads to further energy splitting:
This effect is generally much smaller than the linear Zeeman effect.
Applications
Laboratory spectroscopy
The Zeeman effect has numerous applications in spectroscopy ( electron spin resonance (ESR), nuclear magnetic resonance (NMR), nuclear magnetic resonance spectroscopy , magnetic resonance tomography , Mössbauer spectroscopy, etc.). In atomic absorption spectrometry , the Zeeman effect is used for background compensation. Historically, the Zeeman effect also played an important role in the discovery of the electron - the same charge-to-mass ratios were found in the spectrum as in the free electron observations by Joseph John Thomson and others, and Zeeman's observations came first.
The Zeeman effect is used in the Zeeman slower ( William D. Phillips , Harold Metcalf 1982), a special case of laser cooling, often in advance of a magneto-optical trap .
astronomy
George Ellery Hale demonstrated the existence of strong magnetic fields in sunspots using the Zeeman effect . The picture shows a sunspot on the left. It was resolved spectroscopically along the vertical line. The Fraunhofer line appears almost undisturbed above and below the sunspot . It appears expanded within the sunspot.
A magnetic field B on the sun of 0.1 Tesla causes energy to be split
with Bohr's magneton . It can only be observed in spectrographs with a resolution better than 10 −4 . Magnetograms are recorded in the light of the split magnetic lines. The sun appears gray. Strong deviations in the polarity of the magnetic field are highlighted in black or white and mark active zones.
Magnetic sense in animals
One theory about the magnetic reception of animals assumes that a protein in the retina of birds the magnetic sense brings about the Zeeman effect.
See also
literature
The original works are:
- Pieter Zeeman: On the influence of Magnetism on the Nature of the Light emitted by a Substance. In: Philosophical Magazine. Vol. 43, 1897, p. 226, doi: 10.1080 / 14786449708620985 (Dutch in the negotiations of the Royal Netherlands Academy, Amsterdam 1896, Over den Invloed eener Magnetisatie op den Aard van het door een Stof uitgezonden light ).
- Pieter Zeeman: Doublets and triplets in the spectrum produced by external magnetic forces. In: Philosophical Magazine. Vol. 44, 1897, p. 55, doi: 10.1080 / 14786449708621060 (Dutch in the negotiations of the Royal Netherlands Academy, Amsterdam, Over Doubletten en Tripletten in het Spectrum teweeg brought about necessary Magnetische Krachten I to III, 1897).
- Pieter Zeeman: The Effect of Magnetization on the Nature of Light Emitted by a Substance. In: Nature. Vol. 55, February 11, 1897, p. 347, doi: 10.1038 / 055347a0 .
- EP Lewis: The Effects of a Magnetic Field on Radiation - Memoirs by Faraday, Kerr and Zeeman . Read Books, 2007, ISBN 1-4067-6505-8 ( limited preview in Google Book Search - facsimile collection of some works by M. Faraday, J. Kerr and P. Zeeman).
Web links
- Alexander Fromm, Martin Hörner: Zeeman Effect ( Memento from July 5, 2010 in the Internet Archive ). University of Freiburg, internship attempt, September 8, 2005, accessed on February 2, 2010 (PDF file; 434 kB).
Individual evidence
- ↑ P. Zeeman: About an Influence of Magnetization on the Nature of Light Emitted by a Substance , Negotiations of the Physical Society in Berlin, p. 127, 1896. (The internet source erroneously contains further pages of the volume between the pages of the article.)
- ^ Nobelprize.org: The Nobel Prize in Physics 1902 (accessed November 6, 2012).
- ^ Anne J. Kox: A pioneer of magneto-optics . Physik Journal 14 (2015) No. 6, pp. 51–53.
- ↑ Klaus Hentschel: The discovery of the Zeeman effect , Physikalische Blätter, Vol. 52 pp. 1232-1235, 1996; doi: 10.1002 / phbl.19960521209
- ↑ The exact value is and measured to 12 decimal places, because the small deviation of 2 is a touchstone for quantum electrodynamics ( CODATA ). This deviation was only discovered in 1946 and played practically no role for the Zeeman effect and its applications in spectroscopy, which is why it is not considered here either.
- ↑ Birgit Dalheimer: The Inner Compass , heureka science magazine, accessed on December 17, 2011.