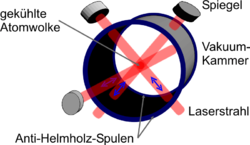
Magneto-optical trap
A magneto-optical trap ( English magneto-optical trap , MOT) is a means of nuclear physics , which is used for cooling and storage of neutral atoms. Cooling here means slowing down the atoms, since the temperature of an individual atom is expressed through its kinetic energy , i.e. its speed. In concrete terms, this means: If a large number of particles (atoms, molecules, etc.) are in thermal equilibrium , the mean kinetic energy of a particle can be expressed in terms of temperature.
In contrast to the storage of charged particles (ions), which can be caught in a Paul or Penning trap by electrical and magnetic fields , the optical force is required for neutral atoms, as this is charge-independent. A MOT consists of six pairs of counter-rotating laser beams that perform the laser cooling . In addition, you need a magnetic field to keep the cooled atoms in place. The magnetic field causes a Zeeman splitting of the atomic levels, which in connection with the laser beams leads to a position-dependent force.
The magneto-optical trap was at the beginning of the experimental research on Bose-Einstein condensation and is used in many experiments to study cold atoms.
Working principle
Cool
Atoms are cooled down according to the principle of laser cooling . This means that the photons from the laser beams transfer their momentum to the atom, which is energetically stimulated in the process. This state of excitation then decays spontaneously or induced. However, while in stimulated emission the direction of the absorbed and emitted photons are the same, in spontaneous emission the direction of the emitted photon is independent of that of the absorbed. Therefore, only absorption processes contribute to cooling, in which spontaneous emission takes place (averaging over many absorption-emission processes). If six pairs of opposing beams are used, as shown above, the atoms can be slowed down and cooled in all spatial directions. The following figure illustrates the braking process schematically:

To catch

If one only applied this principle, one would indeed get cooled atoms, but they would diffuse out of the area of the cooling, since there is only a velocity-dependent, but no position-dependent force. If you add a magnetic field that increases linearly with the distance to the cooling area (e.g. by means of an anti-Helmholtz arrangement of coils ) , a restoring force results due to the Zeeman splitting of the atomic states, which is proportional to the magnetic field the laser. Due to the selection rules of the Zeeman effect , it is now necessary to radiate circularly polarized light, since otherwise no interaction with the atomic states would be possible.
The drawing on the right explains this process in more detail for a simple model system, the ( F = 0 to F = 1 ) transition. The magnetic field leads to a location-dependent splitting of the levels into a higher, a lower and an unchanged state ( m F = ± 1.0 ). Since the laser is red-detuned by Δω with respect to the resonance frequency, it comes into resonance with the lowered or raised state at a certain position. To the left of the cooling region there is a point at which the cooling laser comes into resonance with the lowered state ( m F = +1 ). Due to the selection rules, it can only interact with light of helicity σ + . The same applies to σ - light, to the right of the cooling region with the (m F = -1) state. If one radiates σ + - light from the left and σ - light from the right , a net force results which drives the atoms back into the cooling region.
In the laboratory, the helicities translate into circular polarizations in such a way that a pair of opposing rays each have the same polarization. This fact arises from the fact that the direction of rotation of the light is considered once in relation to the direction of propagation of the beam (polarization of the light) and once in relation to the quantization axis of the atom (helicity σ + or σ - ). The quantization axis is parallel to the magnetic field, so it turns around at the point x = 0 . For the atom, only the direction of rotation with respect to this axis is important, not the direction from which the light comes. The rotation of the quantization axis (when reversing the magnetic field) in the reference system of the atom also leads to a change in the direction of rotation of the light.
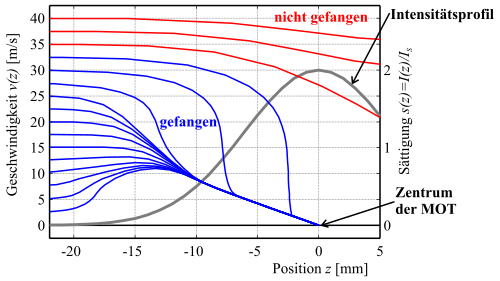
A magneto-optical trap can only catch atoms that are slower than a certain maximum speed. For faster atoms, the braking from the absorption / emission cycles is no longer sufficient and they become slower, but not trapped. This is illustrated in the following graphic, which shows the trajectories (speed v as a function of location z ) of atoms with different initial speeds . Too fast atoms are slowed down, but not caught. The gray profile indicates the intensity profile of the MOT laser (right coordinate axis, I S is the so-called saturation intensity of the transition). The magnetic field was assumed to be linear, which for the central region of a MOT i. A. is a good approximation.
Real atoms
Real atoms normally have several states into which the excited atom can decay, but not all of which interact with the cooling light. In order to prevent the atoms from being lost from the trap as a result of such decays, one or more pump back lasers are used, depending on the atomic species, to transfer these competing states back into the cooling process.
literature
- Harold J. Metcalf , Peter van der Straten: Laser cooling and trapping. Springer, New York NY et al. 1999, ISBN 0-387-98747-9 ( Graduate Texts in contemporary Physics ).
- William D. Phillips : Laser cooling and trapping of neutral atoms. In: Reviews of Modern Physics. 70, 1998, ISSN 0034-6861 , pp. 721-741.
- EL Raab, M. Prentiss, Alex Cable, Steven Chu, DE Pritchard: Trapping of neutral sodium atoms with radiation pressure. In: Physical Review Letters. 59, 1987, ISSN 0031-9007 , pp. 2631-2634, doi : 10.1103 / PhysRevLett.59.2631 .
Web links
- Guide to a laboratory experiment at the University of Colorado (English) ( Memento of 10 June 2010 at the Internet Archive )