laser
Laser (/ lɛɪzər / even / leːzər / or / laːzər /; acronym for English l ight A mplification by S timulated e mission of R adiation , light amplification by stimulated emission of radiation " ) refers to both the physical effect and the device used to generate laser beams.
Laser beams are electromagnetic waves . They differ from the light from a light source used for illumination , for example an incandescent lamp , primarily in the otherwise unattainable combination of high intensity , often a very narrow frequency range ( monochromatic light ), sharp focus of the beam and long coherence length . With a very wide frequency range, extremely short and intense beam pulses with an exact repetition frequency are also possible.
Lasers have many applications in technology and research as well as in daily life (eg. As from simple light pointer laser pointer for presentations) about Distance measuring instruments , cutting and welding tools , reading of optical storage media such as CDs , DVDs and Blu-ray discs , message transmission through on the laser scalpel and other devices using laser light in everyday medical practice.
Lasers are available for radiation in different areas of the electromagnetic spectrum : from microwaves ( maser ) to infrared , visible light , ultraviolet and X-rays . The special properties of the laser beams arise from their generation in the form of a stimulated emission . The laser works like an optical amplifier , typically in resonant feedback . The energy required for this is provided by a laser medium (e.g. crystal, gas or liquid) in which there is an inversion of population due to external energy input. The resonant feedback is usually caused by the fact that the laser medium is located in an electromagnetic resonator for the radiation of a certain direction and wavelength.
In addition to the discrete energy levels of atomic transitions, there are also laser types with continuous energy transitions such as the free-electron laser . Since atomic energy levels are limited to less than 13.6 eV , which corresponds to a limit at the wavelength of 90 nm, the X-ray lasers operating in the X-ray radiation range with wavelengths less than 10 nm require designs with continuous energy transitions.
Basic functions
Basic ingredients
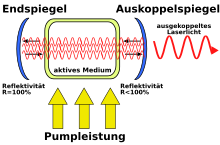
Conceptually, a laser consists of three components:
- Active medium (laser medium)
- In the active medium , the optical transition of excited atoms or molecules into an energetically more favorable state creates photons . The central condition for a laser medium is that a population inversion can be produced. This means that the upper state of the optical transition is more likely to be occupied than the lower. Such a medium must have at least three levels and can be gaseous (e.g. CO 2 ), liquid (e.g. dye solutions) or solid (e.g. ruby crystal , semiconductor material ).
- pump
- A population inversion bring about, must be in the laser medium energy pumped ( English pumping ) are. So that this pumping process does not compete with the stimulated emission, it must be based on a different quantum mechanical transition. Pumping can bring the atoms or molecules of the laser medium into excited states optically ( irradiation of light ) or electrically (e.g. gas discharge , electrical current in laser diodes ) .
- Resonator
- A resonator consists, for example, of two parallel mirrors between which the active laser medium is located. Photons whose propagation is perpendicular to the mirrors remain in the resonator and can therefore trigger (stimulate) the emission of further photons in the active medium several times . A photon created in this way corresponds in all quantum numbers to the triggering photon. Spontaneous photons that leave the resonator, for example transversely, accordingly tend not to stimulate any further photons. This selection of the resonator leads to a narrow beam direction of laser radiation. Some resonators are also wavelength-selective (dichroic mirrors, Bragg gratings) and can thereby further limit the oscillating longitudinal modes. In some high-gain laser media, a resonator is not absolutely necessary to achieve stimulated emission (see super emitters ).
functionality
At first, atoms in the laser medium are transferred from lower energy levels (e.g. ground state ) to higher energy levels, i.e. H. excited states. The mean decay time of the excited states (usually due to spontaneous emission ) should be as long as possible. Thus, the pump energy remains stored there for a “longer” time so that a population inversion can be built up. It is now sufficient to stimulate an atom with a photon with the energy to be emitted so that the excited atom falls back into its ground state and emits a photon of the same energy (i.e. identical wavelength and frequency) and the same phase position as the stimulating photon. Both photons move in the same direction. By doubling the stimulating photon, the laser medium acts like a light amplifier. The “freshly created” second photon can then in turn stimulate other excited atoms to emit, and a chain reaction occurs .
In addition to this amplifier effect, the arrangement is located in a resonator (see below under laser resonator ), which is matched to the desired wavelength due to its dimensions. If a photon passes through the laser medium several times, it has enough chances to stimulate other atoms. The resonator is basically formed from two mirrors at the ends of the arrangement. The direction of the generated light beam is finally determined by these mirrors. One of the two mirrors is partially transparent so that part of the light can exit and be used.
history
Albert Einstein described stimulated emission as a reversal of absorption as early as 1916. In 1928 Rudolf Ladenburg succeeded in proving it experimentally. After that, it was long puzzled whether the effect could be used to intensify the light field, since a population inversion had to occur to achieve the amplification . But this is impossible in a stable two-level system. First a three-level system was considered, and the calculations showed a stability for radiation in the microwave range, realized in 1954 in the Maser by Charles H. Townes , which emits microwave radiation. Afterwards, Townes and Arthur L. Schawlow , among others, worked on the transfer of the maser principle to shorter wavelengths. The first laser - a ruby laser - was completed by Theodore Maiman on May 16, 1960. The first gas laser, the helium-neon laser , was also developed in 1960 ( Ali Javan , William R. Bennett , Donald R. Herriott ).
The term was coined in the late 1950s by Gordon Gould based on the burl; Gould first used the term in his notes in 1957. Early publications called the laser nor optical maser (optical maser).
Further development then led first to various gas lasers ( oxygen , nitrogen , CO 2 lasers , He-Ne lasers) and then to dye lasers (the laser-active medium is liquid) by Fritz P. Schäfer and Peter Sorokin (1966). A further development of crystal technologies enabled a very strong expansion of the useful spectral range. Tunable lasers for approaching a certain wavelength and broadband lasers such as. For example, the titanium-sapphire laser heralded the era of ultrashort pulse lasers with pulse durations of picoseconds and femtoseconds in the 1980s.
The first semiconductor lasers were developed in the 1960s ( Robert N. Hall 1962, Nick Holonyak 1962 in the visible spectral range, Nikolai Basow ), but only practical with the development of semiconductor lasers based on heterostructures (Nobel Prize for Herbert Kroemer , Schores Alfjorow ). In the late 1980s, semiconductor technology enabled ever more durable, highly effective semiconductor laser diodes that are used with low power in CD and DVD drives or in fiber optic data networks and are now gradually used as pump sources with powers up to the kW range replace ineffective lamp excitation of solid-state lasers.
In the 1990s, new pump geometries for high laser powers were realized, such as the disk and fiber lasers . At the turn of the millennium, due to the availability of new manufacturing techniques and outputs of up to 20 kW, the latter were increasingly used in material processing, where they can partially replace the previously used types (CO 2 lasers, lamp-pumped Nd: YAG lasers ).
At the beginning of the 21st century, nonlinear effects were used for the first time to generate attosecond pulses in the X-ray range. This made it possible to follow the chronological processes inside an atom. Most recently, blue and ultraviolet laser diodes were ready for the market.
In the meantime, the laser has become an important instrument in industry, medicine, communication, science and consumer electronics.
Physical basics
In the active medium in the resonator there is a fixed number of atoms or molecules with several, but always the same, energy levels. Two of these levels, referred to as the lower laser level and the upper laser level (where ), form the laser transition . The laser transition is the optical transition whose energy difference corresponds to the frequency of the laser light. The difference between the number of particles in the lower and upper laser level is known as "inversion" and is decisive for the functioning of the laser.
There are two basic conditions that must be met at the same time for a laser to work:
- (Population inversion) - there must be more particles in the upper than in the lower laser level.
- If a resonator is used, the amplification of the laser light due to stimulated emission during one pass through the resonator must be greater than its losses due to absorption , scattering and mirror losses , in particular coupling-out losses . The resonator mirrors must have a reflectivity of less than one on at least one side so that laser light can leave the laser and can be used at all. This decoupling of part of the laser light is referred to as decoupling loss because this portion no longer contributes to further amplification in the laser medium through stimulated emission.
Each transition between the two levels corresponds to the emission or absorption of a photon with the angular frequency , where the energy difference between the two levels is the reduced Planck constant . Such a photon is created during emission, and a corresponding photon is lost during absorption. The choice of the laser medium determines the frequency or the color of the light.
The mathematical description of the occupation takes place using special coupled differential equations , so-called rate equations . These describe the temporal course of the occupation states, i.e. the temporal change of and . The exact form of the rate equations depends on how many energy levels besides the two laser levels are available and used, and on the type of certain approximations .
Two-level system
Two stable energy levels are not enough to construct a laser, as shown below. The consideration of two-level systems, however, provides the basis for considerations of laser media with more than two energy levels at which laser operation is possible. A theoretical two-level system would be pumped directly from the lower to the upper laser level. For a two-level system, the rate equations are:
It is the Einstein coefficient for the spontaneous emission, the Einstein coefficient for absorption and stimulated emission and the intensity of the light in the resonator. The individual terms each stand for the absorption or emission of photons and thus the change in the number of particles in this state. Since inversion is important for laser operation , the difference between these two rate equations is formed, as well as and expressed by and the conservation quantity:
After a certain time an equilibrium will be established in the occupations, whereby the temporal change of the inversion becomes vanishingly small ( fixed point ). In order to find this point of equilibrium , the resulting equation can then be transformed into:
where the saturation intensity is called (the index stands for "stationary"). This population inversion is always positive, regardless of how great the intensity becomes. This means that there are always fewer particles in the upper laser level than in the lower. Hence, population inversion is not possible in a stable two-level system. It is therefore impossible to construct a laser in this way.
The Einstein coefficients provide a clear explanation. As soon as half of all particles in the laser medium are in the upper laser level, the probability that an atom in the lower laser level will absorb a photon is just as high as the probability that an atom in the upper laser level emits a photon through stimulated emission. The additional spontaneous emission ensures that not even this theoretical limit is reached.
Three-level system
In addition to the two levels in the two-level system, there is another energy level above the upper laser level in a three- level system, so that applies . This time the pumping takes place from the lower laser level to the new level . For the third level, the condition is also set that it passes into the state much faster than after , so that it applies or again . This rapid transition occurs either without radiation or via spontaneous emission. Similar to the two-level system, rate equations are set up here as well:
In contrast to the two-level system, there is no stimulated emission from the pumping process. Again, these rate equations can be transformed into an equation for the occupation by forming the difference, expressing it through and and then considering the equilibrium state :
This equation becomes negative ( ) as soon as the condition is met. This means that in a three-level system there can be more particles in the upper laser level and therefore population inversion is possible. The prerequisite is a high intensity of the light in the resonator. Three-level lasers are thus possible.
Four level system
With a four-level system, there is an additional energy level compared to the three-level system. This is below the lower laser level , so that applies . The transition from to has again as a condition that it happens very quickly. This changes the approximate condition for the total number of particles to , and the equation for the population becomes to . The pumping process happens from to . The rate equations thus result in:
Here, too, it is again possible to express and through and as well as to set the equilibrium condition and to resolve it:
In this case, the occupation is always negative. This means that an externally excited four-level system is very suitable as a laser medium. Practically all modern lasers are designed as four- or multi-level systems.
Laser resonator
In a laser, the radiation, which was initially initiated by spontaneous emission, is repeatedly guided through the area in which population inversion prevails by a suitable arrangement of two mirrors. Such an arrangement is called an optical resonator or laser resonator. By constantly moving back and forth, sufficient amplification can be achieved to exceed the laser threshold . The laser threshold can only be exceeded if the gain in the resonator is greater than the loss (e.g. due to spontaneous emission, scattering and decoupled power). In addition to the population inversion, this condition is the second fundamental requirement for a laser to function.
In the simplest case, a laser resonator consists of two mirrors, between which the radiation is reflected so that the path through the laser medium is lengthened. As a result, a photon can very often cause stimulated emission. One of the two mirrors is partially transparent and is called a decoupling mirror or decoupler . This ensures that part of the radiation can leave the device as a laser beam. Laser media with very high amplification can also work with only one mirror or without a mirror.
In the resonator only frequencies are amplified which fulfill the resonance condition, for which the following applies:
Here is a natural number and the length of the resonator. Other frequencies are canceled out by destructive interference. Another construction is the ring resonator , in which the light passes through a closed path by multiple reflection.
The quality of the resonator (i.e. the ratio between radiation reflected back and forth to exiting radiation) must be particularly high in the case of low-amplifying media. An example of this is the helium-neon laser . The resonator quality can often be influenced in a time-dependent manner by means of optical components located in it, but also with regard to the wavelength and the lateral beam profile, in order to achieve good beam quality , frequency constancy and coherence as well as pulse shaping of the laser beam. Such components are e.g. B. diaphragms, optical switches ( quality switches ) or frequency-selective end mirrors.
The resonator stability can be calculated with simple resonators (mirror - active medium - mirror) with the so-called g-factors. They are defined as:
Here and are the radii of curvature of the two resonator mirrors and the total length of the resonator. The stability condition is
A paraxial beam does not leave the resonator even after any number of reflections. If the result is 0 or 1, the resonator is borderline stable. An example of this is the confocal ( ), hemispherical ( ), concentric ( ) or plane-plane resonator ( ), which is also known as the Fabry-Perot resonator . In practice, these types of lasers are very difficult to adjust and usually only work because other lens effects lead the resonator into the area of stability. Such an effect can be, for example, a thermal lens effect, in which a thermal lens is created by a temperature gradient in the resonator. Stable resonators have a positive effect on the beam quality and the coherence properties of the laser beam. The disadvantage is the poor utilization of the laser medium, since the light beam hits the same particles again and again instead of exciting new particles.
For unstable resonators, or . For these, the diffraction losses are very high, but unstable resonators can be used advantageously with a laser medium with a large diameter, since these generate a uniform intensity distribution in the resonator. A prerequisite for this, however, is a high gain in the laser medium. Unstable resonators are therefore mostly used in lasers which have a high gain per resonator cycle and for which high output power and less the beam quality are decisive. The asymmetrical confocal unstable resonator is of particular importance because it provides a parallel output beam.
Since a not inconsiderable part of the energy used is converted into heat when generating laser radiation, efficient cooling of the laser active medium must always be ensured when designing laser resonators, especially in the high-performance range. Optical effects caused by a temperature gradient in the laser active medium also play a major role here, as a result of which the focus position within the resonator depends on its temperature. In the case of gas lasers, efficient cooling can be achieved, for example, by constantly circulating the gas used in order to cool it outside the actual laser.
Longitudinal modes
Different waveforms are called modes . The vibration along the direction of propagation of the radiation is called longitudinal. Expressed figuratively, these are intensity peaks and valleys at a distance of half a wavelength. With a He-Ne laser a few centimeters long you could count around 600,000 intensity mountains between the mirrors, with a short laser diode only a few thousand.
Depending on the design, certain wavelengths and their multiples are particularly amplified by the resonator, because there is a standing wave between the mirrors only for certain wavelengths .
The picture shows the intensity distribution around the fundamental mode (given as mean intensity as a function of frequency ).
More precisely, the following relationship applies to the possible light frequencies in a laser resonator:
- ,
is the permissible frequency of the -th mode, the speed of light and the resonator length (distance between the resonator mirrors). In this formula you can replace the frequency with the more common term wavelength and get for the possible wavelengths in a resonator:
An optical resonator therefore acts like a comb filter that amplifies or weakens certain successive frequencies.
Due to the Gaussian Doppler broadening of the emission line, which is actually sharp, the Gaussian envelope is created over a certain number of "comb teeth". Due to the above resonator property (and the subsequent Doppler broadening), several partial lines of the emission line of the active medium are amplified in the resonator. The individual partial lines amplified in the resonator have a Lorentz profile with very small line widths because of the great length of the wave trains in the resonator and because interference effects such as the Doppler effect take a back seat at resonance . This gives the spectrum shown opposite with several Lorentz curves (the so-called laser modes) with a Gaussian envelope. However, since a minimum intensity is necessary so that amplification can still take place in the resonator, only a limited number of modes are obtained, since modes that are too far away from the center of the line are not intense enough to be amplified.
The frequency spacing between two neighboring modes is:
A state can also arise in which the beam has to travel back and forth through the resonator twice in order to get back to the starting point. This doubles the effective resonator length and halves the mode spacings .
The half width of the maxima is
The factor that occurs is called finesse and is the key figure for resonators, which indicates the spectral resolution. indicates the free spectral range of the resonator. If the losses in the resonator are neglected, the finesse only depends on the reflection factor of the mirrors:
Depending on the mirrors used, the finesse can take on values from about 10 to several 100,000.
Multiple longitudinal modes are undesirable in many applications. Shortening the resonator length in order to generate only one mode, however, usually makes no sense, since the desired light output cannot be achieved in this way. One remedy is to introduce a so-called etalon into the resonator . In principle, the etalon represents a “resonator in a resonator”, which only amplifies waves of the desired mode, but suppresses other modes. In this case one speaks of monomode or singlemode lasers (as opposed to multimode lasers).
Transverse modes
The distribution of the phase position of the waves perpendicular to the direction of propagation is called transverse modes. So if a mode develops that does not fill the space perpendicular to the resonator mirrors, but runs somewhat obliquely, the light and resonator path becomes longer and the frequency shifts somewhat. On the one hand, this leads to competition for excited medium molecules between the various frequencies (mode competition), and on the other hand, standing waves can develop that have nodal lines within the laser profile. Whether and how they occur in a laser beam can be determined by optical components such as polarization filters or diffractive optical elements .
The type of transverse modes depends on the design of the laser:
- When using flat reflectors, TEM modes occur, which means that the electromagnetic wave has no electrical or magnetic components in the direction of propagation. This also applies to the propagation of light in free space.
- The majority of lasers use curved mirrors; hybrid modes then almost always occur, which also have electrical and magnetic components in the direction of propagation.
( Pure TE or TM modes can also be observed in waveguides with a metallic shell, because electrical currents can flow in the shell surface.)
With a cylindrical cross-section of the laser, the beam intensity ideally has a Gaussian profile; this mode is called TEM 00 mode ( see also: Modes # Other acoustic modes ). However, other profiles with angular and radial dependencies can also occur, which can be calculated using Laguerre polynomials . If this cylindrical symmetry is disturbed by a polarization filter or Brewster window , rectangular symmetries occur which are calculated using Hermitian polynomials . Depending on the number of their node lines in the horizontal and vertical directions, they are referred to as TEM xy mode. For these modes, the light path through the resonator to the starting point is partly different, that is, the resonator length appears to have changed. This can lead to a falsification of the longitudinal mode spectra in that the spectra of different transverse modes overlap.
Properties of laser radiation

1. Near field with fill factor and energy density ,
2. Beam quality in the far field,
3. Pulse duration and spectral width ( line width )
The beam properties of a laser beam are essentially determined by the type of laser resonator, in particular the geometry of the active medium and the mirror arrangement play an important role. With lasers it is possible to control or manipulate light to a high degree ( brilliance , intensity , direction , frequency , polarization , phase , time ). It is therefore not possible to make a general statement about the beam properties. It is also incorrect that a laser beam always has to be a tightly bundled beam with a narrow frequency range, which is often assumed to be the case. However, depending on the objective, such rays can be generated. An outstanding, general property, however, is the possibility of strong bundling, with which very high power densities can be achieved. The lateral power density distribution of laser beams is a Gaussian profile ( Gaussian beam ) with good beam quality .
In general, it can be said of the beam properties that laser beams are characterized by many differences compared to conventional light sources, which are mentioned below.
coherence
With a normal incandescent lamp, light waves are not only emitted with different wavelengths, but also in an indefinite phase relation to one another. With a laser, on the other hand, the waves are almost phase-synchronized with one another. The waves are almost in phase over more or less long stretches ( coherence length ), which is used, for example, in holography .
polarization
The polarization of laser beams is mostly linear due to polarizing optical components in the resonator (inclined deflecting mirror and Brewster window , low height of the resonator in semiconductor lasers). This is often desirable in order to be able to carry out polarization-dependent coupling and beam splitting. When cutting metals, however, polarization-dependent absorption occurs in the cutting gap , particularly with the linearly polarized CO 2 laser radiation , which results in poor and direction-dependent cut edge quality. For this reason, circular polarization is used when cutting metal, which is achieved by phase-rotating retardation plates in the beam path of the laser beam.
Frequency, wavelength
The frequency of laser radiation is determined by the active medium and its energy transitions suitable for lasing. There are substances that can be excited to laser at many wavelengths - but mostly particularly well at one wavelength. Lasers can be very narrow-band beam sources, but the gain bandwidth (for carbon dioxide lasers, for example, 9 to 11 µm) is usually higher than the bandwidth of the emitted radiation - either the laser oscillates by itself at the maximum of the gain bandwidth (for carbon dioxide lasers, for example 10.6 µm) on or by means of frequency-determining elements for a narrow-band emission on a single frequency. Extreme narrowing is e.g. B. in the interferometric length measurement by means of lasers of importance. With extreme broadband one speaks of supercontinuum lasers, which z. B. be used in optical coherence tomography and for generating frequency combs. The minimum achievable bandwidth is described by the fundamental laser line width . The Schawlow-Townes limit is a four-fold approximation of this fundamental laser line width.
Laser types according to the waveform
Continuous wave
A continuous wave laser is a laser that, in contrast to pulse lasers, emits a light wave of constant intensity.
Laser radiation from the continuous wave lasers ( English continuous-wave laser, CW laser ) is in the ideal case narrow band (monochrome, color), d. H. it consists only of radiation of one wavelength . In particular, continuous wave laser radiation from stable laser resonators is coherent in time or longitudinally (along its direction of propagation) due to the multiple rotation, which means that the transmitted wave trains not only vibrate at the same frequency , but also in phase over a long distance (the coherence length ) are constant. As a result, such light shows particularly pronounced interference phenomena .
During the settling process of the continuous wave laser, spiking often occurs, an irregular emission of laser pulses. A mode-locked laser uses this behavior in a targeted manner . B. triggers or synchronized.
Pulse
In contrast to the continuous wave laser, a pulsed laser generates pulsating radiation. Pulses can be generated by pulsed excitation or by measures in the laser itself ( Q-switching ). In the case of very short pulses, the active medium principally requires a larger gain bandwidth within which the frequencies involved are coupled (mode coupling) and combine to form a pulse. The shorter the pulse duration, the wider the spectrum generated , according to the laws of Fourier analysis , and the wider the frequency band within which the active medium can amplify. The lowest achievable pulse durations are in the order of magnitude of femtoseconds and attoseconds (→ femtosecond laser ).
Lasers can also synchronize themselves to emit a pulse train if, for example, a non-linear (saturable) absorber is present in the resonator. The repetition frequency with which the pulses are generated in such a laser depends u. a. at the instantaneous Kerr lens -Modenkopplung ( English Kerr lens mode lock-in , a process for producing a stable pulse train of pulses of short duration) on the resonator length: In a resonator having a length of half a meter, this approximately 300 MHz is - the period corresponds to the pulse running back and forth in the resonator. The peak power increases with every revolution, the pulse duration remains very short by itself. For example, individual pulses are released from such pulsed lasers using optical switches and further amplified. With further measures, it is possible to generate peak power up to the petawatt range, which can only be transmitted and focused undisturbed in a vacuum. Air is ionized by the high electric field strength of light .
The quality modulation ( Q-switching ) of the resonator with acousto-optical Q- switches or Pockels cells are further techniques for generating high-energy laser pulses with short duration: The stimulated emission is initially suppressed, and then when the population inversion has increased due to the pumping (high, stored in the active medium Energy) suddenly.
Classification based on the laser medium
| Rough classification of laser types | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lasers are often categorized and named based on the properties of the optical laser medium used . The roughest classification is based on the state of aggregation .
Important gas lasers are, for example, the helium-neon laser emitting at 632.8 nm and the carbon dioxide laser emitting at 10.6 μm . Special classes of gas lasers are excimer lasers , in which the laser medium is an excimer molecule, and metal vapor lasers , in which the gaseous laser medium must first be obtained by evaporating metal.
Lasers with a liquid laser medium are known as dye lasers . These lasers are characterized by a very large, continuous and tunable range of wavelengths. The dyes used are in many cases stilbenes , coumarins and rhodamines .
The group of solid-state lasers includes lasers whose laser medium is crystals. This can include doped glass , yttrium aluminum garnet and other host crystals or semiconductors . Important examples are the Nd: YAG laser , the laser diode and the titanium: sapphire laser . Frequently used dopants are titanium , chromium and neodymium . There are many options for the shape of the solid, such as: B. the rod laser , slab laser , fiber laser and the disk laser . The color center lasers are a special form of solid-state lasers, which function similarly, but use color centers to generate the laser transitions.
The free electron laser (FEL) is a special form . It is a synchrotron radiation source that emits directed radiation in the microwave range up to the X-ray range . However, an FEL is not a laser in the strict sense of the word, as the radiation is not generated by stimulated emission in a laser medium.
Applications

Lasers are used in very many areas of life and work, research and industrial branches and medical fields of activity. The following sections provide a rough overview of the most important areas of application for laser technology.
Everyday life and entertainment
Lasers have found their way into many areas of daily life. There are laser diodes in every laser printer and all optical drives , such as CD , DVD and Blu-ray Disc players.
Laser pointers contain weak lasers with visible wavelengths. In discotheques and laser shows , lasers with an output power of up to several watts are used for light effects. In the so-called laser harp , a fanned out laser beam is used as an input device to control musical instruments. In Planetariums laser are separated as projectors used. One variant is the " All Dome Laser Image Projector ", as used in the Jena planetarium, for example . In some barcode scanners , lasers are used to scan the barcodes .
Data acquisition and transmission
An important area of application for diode lasers and fiber lasers is data transmission using optical fibers . The optical radio relay is possible, but not widespread because of the susceptibility to interference. The transmission of data between satellites or spacecraft by means of lasers enables a much higher data rate than the previously common radio waves due to the higher frequency. The technology has so far been used in particular as a relay, for example by Artemis . The communication to earth with laser is hindered by the atmosphere. The associated technology is still in the testing phase, but could play a bigger role in the future.
Further applications are holography and laser scanning for measuring objects or in leveling devices .
Industry and material processing
In industry and manufacturing technology , lasers are used for various manufacturing processes (DIN 8580). For this purpose, they are operated on a laser processing machine or a laser scanner. Lasers are suitable for forming , cutting , joining , coating and changing the properties of a wide variety of materials, such as wood, plastic, paper and metals.
Among the most important methods include laser sintering , the stereolithography , the laser beam bending and laser-assisted bending , the laser cutting and drilling , the laser ablation , the laser trimming , laser beam welding , surfacing and brazing, the laser marking , the laser spraying and pulsed laser , the laser polishing .
Furthermore, structures in the micrometer and submicrometer range can be written on photosensitive materials with lasers. Using microphotolithographic systems, high-resolution templates (masks) are created for various applications using the direct writing process. B. be copied to the final materials by means of broadband high-power lasers in production. Other applications include the direct writing of patterns on silicon - wafers in low quantities or the writing patterns on photosensitive films (eg. Strain gauges ) a. Screen masks , circuit boards , integrated circuits and sensors can be produced in this way .
medicine
In general medicine , the laser is mainly used in diagnosis, e.g. B. when measuring blood flow ( flowmetry ) and circulation. There are also low-level laser therapy devices for treating wounds and pain.
In ophthalmology , laser light with different wavelengths is used, with wavelength, exposure time (exposure time) and energy influencing the physical reaction and penetration depth. The argon laser is used with its thermal effects to prevent coagulation (e.g. in the case of diabetic retinopathy, thrombosis), the formation of new vessels or to perform retinopexy (welding of tissue layers in the event of a retinal hole or detachment). The neodymium-YAG laser and femto-LASER cause a precisely, narrowly circumscribed tissue tear (photodisruption) due to the high-energy ultrashort suprapulse and the excimer laser, through its own phenomenon of tissue evaporation (photoablation / sublimation), a reshaping of the corneal surface (e.g. B. PRK or LASIK) to eliminate the ametropia. The femtosecond laser cataract surgery is a new method in surgery of cataracts ( cataract ), which is in some important steps during this engagement of particularly high precision. In addition, three-dimensional imaging processes such as optical coherence tomography (OCT) or online pachymetry, optical path measurement and photo documentation of all eye structures with a resolution in the micrometer range are possible with the laser.
In surgery , vascular surgery and phlebology , the laser is mainly used in endoscopy or as a laser scalpel . Another application is the treatment of defective veins ( varicose veins ). The laser can be used endovenous (laser light guide is inserted into the vein). This laser treatment method replaces the removal of the vein with " stripping ". In many cases, laser treatment is gentler and can be carried out on an outpatient basis.
In dermatology , cuts and sclerosing can be carried out with laser beams . Blood vessels can be coagulated by lasers of specific wavelengths. Pigment spots can be removed or selectively destroyed with the help of ablating (= peeling) lasers. Subcutaneous (= located under the skin) pigment can be destroyed with the help of an ultra-short pulsed laser and thus removed without seriously damaging the skin surface. By using long-pulsed lasers, hair roots can be permanently destroyed by epilation . Lasers are also used for the targeted treatment of inflammatory skin diseases, primarily psoriasis ( psoriasis ). Superficial unevenness of the skin (nodules, wrinkles) are smoothed out (resurfacing) for the cosmetic improvement of the skin's appearance. Laser light can also be used to selectively heat the dermal parts, which is primarily intended to help build up collagen to tighten the skin (“subsurfacing”).
In ear, nose and throat medicine , lasers are used to remove changes to the vocal cords during microlaryngoscopy , as well as to partially remove the tonsils ( tonsillotomy ) and tumors in the mouth and throat (e.g. in tongue carcinoma). During otosclerosis surgery , lasers are used to perforate the stapes footplate.
In dentistry , lasers can be used to remove hard tooth substance ("drilling without a drill") or in periodontology (germ reduction and concretion removal in inflamed gum pockets ). Diode lasers are used in dentistry for surgical interventions, e.g. B. lip frenulum removal, used for germ reduction in endodontics (root canal treatment) or for tooth whitening (bleaching). Advantages of laser treatment compared to the conventional method are that the patient experiences less pain, the setting of sutures is sometimes superfluous, there is less bleeding because the wound is sclerosed and the treated area is simultaneously decontaminated (germ-free). In some cases, however, better studies with a higher level of evidence are required to assess the benefits of the laser.
In cancer therapy it is used for photodynamic therapy ; in urology for the treatment of kidney and ureter stones and the prostate . The laser microdissection is a method for obtaining small samples of tissue sections or cell cultures.
Techniques still being researched include: a. attempts to grow nerves in a targeted manner using laser light.
The safety regulations for medical lasers are dealt with in EN 60601-2-22 .
Measurement and control technology
A number of precise measuring devices for distances and other quantities work with lasers. They are used, for example, in tunnel construction , in construction and for measuring the machine geometry of machine tools and systems.
Other measuring devices based on lasers are coherence radar , optical distance measurements using light detection and ranging (Lidar) and laser guns , laser-based fire detectors , electronic speckle pattern interferometry (ESPI) for shape detection , laser microphones , laser extensometers , laser Doppler anemometry and particle image velocimetry for measuring flow velocities , laser Doppler vibrometer for non-contact vibration measurement , laser surface velocimeter , laser cloud altimeter in meteorology and laser gyro .
Energy Technology
Lasers can be used to enrich uranium for the production of nuclear fuel .
military
In the military and in the armaments industry , lasers are used for communication and measurement purposes, as in everyday life, but are also used as weapons or weapon-supporting technology. These include aiming aids for laser-guided bombs and rockets as well as for generating target markings on handguns (for example on the AM180 ), "laser rifles" for temporary blinding and high-energy lasers for defense against missiles (laser cannons) (see also energy weapon and space weapon ).
High-performance laser systems in the wavelength range around 1 micrometer serve as “drivers” in systems for inertial fusion such as the National Ignition Facility .
2014 was the US Navy the first laser weapon ( English Laser Weapon System , in short Laws) on the USS Ponce put into operation. In published videos, the weapon is tested on unmanned flying objects and inflatable boats, which start to burn after a short time. In 2018, the Russian laser weapon Peresvet , which is supposed to fight drones, planes and missiles, entered service.
Science and Research
In modern research in physics , chemistry and biology and their respective sub-areas, lasers are one of the most important tools. In laser spectroscopy , lasers are used for laser cooling and the determination of energy levels in atoms and molecules , for density measurement in gases and plasmas, or for determining material properties. Specific laser spectroscopic methods are, for example, atomic spectroscopy , the tunable diode laser absorption spectroscopy , the Raman spectroscopy and nonlinear Raman spectroscopy . Effects such as those predicted by non-linear optics can only be achieved with lasers. Isotope separations , such as AVLIS and MLIS , are also only possible with lasers.
In the surveying laser used for measurement of the earth and the plate tectonics , for example using tacheometers , laser tracker , channel laser , Satellite Laser Ranging and LaserDisto .
The optical tweezers and the two-photon microscope are applications in cell research .
In astronomy , lasers are used for the precise adjustment of optical components and instruments and for the observation of spatial objects. These include laser telescopes , laser theodolites and riflescopes as well as the measurement of the moon's movement using lunar laser ranging .
In super-resolution microscopy with the STED microscope , for which Stefan Hell received the Nobel Prize for Chemistry (with others) in 2014 , two confocal laser beams are used to scan areas with a few atomic diameters.
Homogenization
In some applications, a spatially homogeneous profile is necessary. The laser beam can then be homogenized for the purpose of creating an intensity distribution of the laser radiation that is as uniform as possible over the entire processing spot. A Gaussian profile of the intensity distribution that is initially present, for example, is to be converted into an almost rectangular profile with the least possible inhomogeneity. More often, however, one would like to homogenize irregular and unstable beam profiles. The goal is the even illumination of a surface, for example for heat treatment.
hazards
Health hazards

Lasers can due to the properties of their radiation and due to their z. Sometimes extremely concentrated electromagnetic power can cause biological damage. Therefore, lasers are to be provided with standardized warning notices depending on the laser class . A distinction is made here between the wavelengths and exposure times that lead to characteristic violations and violation threshold values of the power or energy density.
Users and system builders must consider direct, indirect (unintentionally directed reflected ) and scattered radiation (unintentionally diffuse reflected ) with regard to these limit values.
Possible damage:
- The medical use of lasers can cause inflammation of existing or formed gases.
- In addition to the damage mentioned, lasers in the ultraviolet range also cause photochemical changes in the tissue. These include symptoms similar to sunburn with the risk of cancer development as well as clouding of the cornea, the lens of the eye and the vitreous humor.
- During laser material processing, pyrolysis and evaporation sometimes produce highly toxic gases, dusts and aerosols that have to be extracted and filtered.
- Laser beams in the near-infrared range (around 1000 nm) or their scattered radiation penetrate deep under the skin and can cause painless, poorly healing burns in the subcutaneous tissue.
- Burns in the eye: Even at relatively low power (a few milliwatts ) of a wavelength for which the eye is transparent (approx. 350 to 1200 nm), partial blindness occurs in the unprotected eye due to retinal damage, as the parallel laser beam focuses on the retina through the eye lens becomes. Scattered radiation from stronger lasers in this wavelength range is also dangerous. Damage is often not noticed, but only discovered by the ophthalmologist.
- Burns of eyes and skin: If laser beams or their scattered radiation of a wavelength for which the skin and cornea are not transparent (from about> 1400 nm), superficial burns or charring occur with the corresponding power density.
The risk from laser radiation on machines for laser material processing is often assessed according to the Machinery Directive and usually results in Category 4 or Safety Level 3 (also Safety Integrity Level 3, SIL-3 for short) on the risk graph .
Property damage
With sufficient power or focus, laser beams can cause fires and explosions. Highly brilliant lasers for material processing can cause damage to components or walls that are far outside their focal plane if the control system (for example a robot) fails.
Hazard prevention
Every facility in Germany that uses lasers from class 3R must name an instructed person, a laser safety officer , who knows and monitors the dangers and the safe use of lasers.
It is often not possible to completely shield the radiation from the laser by enclosing the machine or the experiment. Access doors must therefore be electrically monitored or locked as long as the laser can emit dangerous radiation. Even light grid can be used to shut off when the scattered radiation is sufficiently low.
Observation windows and protective goggles often allow observation while the laser is switched on if the scattered radiation is low, and consist of filter materials that are at least partially transparent for visible wavelengths, but non-transparent for the specific laser wavelength.
Laser classes
Laser devices are divided into classes according to the harmful biological effects of laser radiation. The definition of limit values at which no damage is to be expected is decisive for the national and international laser classes. In addition to the American ANSI standard, the International Commission on Non-Ionizing Radiation Protection issues limit values in the spectral range between 400 and 1400 nm.
In the case of non-ionizing radiation, the thermal output per area and the specific wavelength-dependent absorption properties of the tissue (skin and retina, cornea, vitreous and lens of the eye) are decisive. By focusing the eye lens, the danger in the visible and especially in the adjacent infrared range is increased.
Above 1.4 µm wavelength, the radiation is absorbed over a large area in the cornea . It provides protection for the retina of the eye. However, the absorption depth is reduced to less than 0.1 mm at 3 µm wavelength, which can damage the cornea. For this reason, i.e. the wavelength range from 1.5 to 2 microns eye safe ( English eye safe ).
Below 1.4 µm, the cornea, skin and underlying tissue are partially transparent in the range of 1200 nm (near infrared) to red (700 nm), so that deep damage can occur here, the development of which is often not noticed because there is no sensation of heat there. Damage to the retina caused by near-infrared laser radiation is also often not noticed and only discovered through medical eye examinations provided for the relevant workplaces.
At wavelengths below about 400 nm, organic molecule bonds are destroyed, the depth of absorption in the tissue shifts to the surface of the skin and eyes with a shorter wavelength. Lens and corneal opacities and damage to the skin, comparable to sunburn, occur even with low thermal power densities. Accordingly, the limit values of the power density at these short wavelengths are lower than, for example, in the mid-infrared.
The classification of laser devices and systems is based on the maximum power or energy densities that occur, depending on whether they are continuous or pulsed lasers. The duration of exposure and the wavelength are also decisive.
Classification according to DIN EN 60825-1

The specified services only apply to point sources and strongly collimated laser radiation. With extended sources and divergent radiation, higher powers are permissible.
The lasers are divided into device classes according to their danger to humans. The classification according to DIN EN 60825-1 is carried out by the manufacturer. (The old classification according to DIN VDE 0837 (→ below) may no longer be used for new lasers.)
| class | description |
|---|---|
| 1 | The accessible laser radiation is harmless, or the laser is located in a closed housing |
| 1C | The accessible laser radiation is harmless to the eye, but in special cases dangerous to the skin. |
| 1M | The accessible laser radiation is harmless as long as no optical instruments such as magnifying glasses or binoculars are used. |
| 2 | The accessible laser radiation is only in the visible spectral range (400 nm to 700 nm). Short-term exposure (up to 0.25 s) is also harmless to the eye. |
| 2M | Like class 2, as long as no optical instruments such as magnifying glasses or binoculars are used. |
| 3R | The accessible laser radiation is dangerous to the eye. |
| 3B | The accessible laser radiation is dangerous for the eyes and in special cases also for the skin. Diffuse scattered light is generally harmless. (Laser from CD / DVD burners; laser radiation, however, not directly accessible) |
| 4th | The accessible laser radiation is very dangerous to the eye and dangerous to the skin. Diffusely scattered radiation can also be dangerous. There is a risk of fire or explosion when using this laser radiation . (Material processing, research laser) |
Comment on laser classes 2 and 2M: A scientific study showed that the eyelid closing reflex (this occurs within 0.25 s; prolonged exposure to radiation damages the eye) was only present in approx. 20% of the test persons. The presence of the blink reflex cannot therefore be assumed as a rule.
Note on the power: Lasers that represent extended light sources and / or emit divergent radiation can allow far higher powers than collimated lasers of the same class. So z. E.g. on page 67 of EN 60825-1: 2007 example B.3.2 is given, in which a strongly divergent 12 mW laser diode (wavelength 900 nm) is classified according to class 1M.
Classification according to DIN VDE 0837
Until March 1997 the laser classes according to DIN VDE 0837 were in effect in Germany. This classification is still in use in the USA today.
| class | description |
|---|---|
| 1 | corresponds to class 1 according to EN 60825-1 |
| 2 | corresponds to class 2 according to EN 60825-1 Lasers in this class may now be classified in 1M. |
| 3a | The accessible laser radiation is dangerous for the eye if the beam cross-section is reduced by optical instruments. If this is not the case, the emitted laser radiation is harmless in the visible spectral range (400 nm to 700 nm) with short-term irradiation times (up to 0.25 s), and in the other spectral ranges also with long-term irradiation. Depending on the wavelength, these lasers are mostly classified in class 2M or 3R today. |
| 3b | corresponds to class 3B according to EN 60825-1 |
| 4th | corresponds to class 4 according to EN 60825-1 |
literature
- Fritz Kurt Kneubühl, Markus Werner Sigrist: Laser. 7th edition. Teubner, Wiesbaden 2008, ISBN 3-8351-0145-5 .
- Jürgen Eichler , Hans Joachim Eichler : Laser. Designs, beam guidance, applications. 7th edition. Berlin / Heidelberg, Springer 2010, ISBN 3-642-10461-4 .
- Jeff Hecht: Beam: The Race to Make the Laser , Oxford UP 2005
- Anthony E. Siegman : Lasers . University Science Books, Mill Valley, CA 1986, ISBN 0-935702-11-3 .
- William T. Silfvast: Laser Fundamentals. 2nd Edition. Cambridge University Press, Cambridge 2004, ISBN 0-521-83345-0 .
- Axel Donges: Physical basics of laser technology. Shaker, Aachen 2007, ISBN 978-3-8322-6392-8 .
- Charles H. Townes: How the Laser Happened. Oxford University Press, New York / Oxford 1999, ISBN 0-19-512268-2 .
- Ute Mauch: Laser medicine. In: Werner E. Gerabek , Bernhard D. Haage, Gundolf Keil , Wolfgang Wegner (eds.): Enzyklopädie Medizingeschichte. De Gruyter, Berlin / New York 2005, ISBN 3-11-015714-4 , p. 827 f.
Web links
- Laser in the Encyclopedia of Laser Physics and Technology (Engl.)
- Different types of semiconductor lasers - overview of the available wavelengths of semiconductor lasers
- Sam's Laser FAQ - Collection of technical documentation and repair instructions
- LaserFest - Website of the American Physical Society on the occasion of the 50th anniversary of the laser
- Laser - light in formation, video about the laser on Youtube, posted by the Max Planck Society
- Video: what is a laser? . Leibniz Universität Hannover 2011, made available by the Technical Information Library (TIB), doi : 10.5446 / 393 .
See also
Individual evidence
- ↑ a b c d e f g Patrick Voss-de Haan: Laser. In: Spektrum.de. 1998, accessed November 7, 2019 .
- ^ FK Kneubühl, MW Sigrist: Laser. 3. Edition. Teubner, 1991, p. 4.
- ^ TH Maiman: Stimulated Optical Radiation in Ruby. In: Nature. 187, 4736, 1960, pp. 493-494.
- ^ R. G Gould: The LASER, light amplification by stimulated emission of radiation . In: The Ann Arbor Conference on Optical Pumping . 1959.
- ↑ A. Javan, WR Bennet, DR Herriot: Population Inversion and Continuous Optical Maser Oscillation in a Gas Discharge Containing a He-Ne Mixture. In: Phys. Rev. Lett. 6, 1961, pp. 106-110.
- ↑ J. Eichler, HJ Eichler: Laser - designs, beam guides, applications . 7th edition. Springer Verlag, 2010, p. 275, equation (13.31)
- ^ T. Graf: Laser. Basics of laser beam sources. 1st edition. Vieweg + Teubner, 2009, pp. 189ff.
- ↑ a b M. Pollnau, M. Eichhorn: coherence Spectral Part I: Passive resonator linewidth, fundamental laser linewidth, and Schawlow-Townes approximation . In: Progress in Quantum Electronics . In press, Nr. Journal Pre-proof, 2020, p. 100255. doi : 10.1016 / j.pquantelec.2020.100255 .
- ^ AL Schawlow, CH Townes: Infrared and optical masers . In: Physical Review . 112, No. 6, 1958, pp. 1940-1949. doi : 10.1103 / PhysRev.112.1940 .
- ↑ Burkhard Dick, Ronald D. Gerste, Tim Schultz: Femtosecond Laser in Ophthalmology. Thieme, New York 2018, ISBN 978-1-62623-236-5 .
- ^ Cochrane Library meta-study
- ^ Non-Lethal Ocular Disruptor. - green glare laser. In: alfalight.com (PDF)
- ↑ Homogenization of laser beams (PDF; 567 kB).
- ↑ Revision of Guidelines on Limits of Exposure to Laser Radiation of Wavelengths between 400 nm and 1.4 mm. (PDF; 1.7 MB) International Commission on Non-Ionizing Radiation Protection, March 30, 2000, accessed on December 14, 2017 .
- ↑ German Institute for Standardization e. V .: DIN EN 60825-1 (VDE 0837-1): 2015-07 . Ed .: DIN and VDE. Correction 3rd edition. Beuth Verlag, Berlin June 19, 2014, p. 23, 31 f .
- ↑ H.-D. Reidenbach, K. Dollinger, J. Hofmann: Review of the laser classification taking into account the eyelid-closing reflex . In: Series of publications by the Federal Institute for Occupational Safety and Health . Fb 985. Wirtschaftsverlag NW, Bremerhaven 2003, ISBN 978-3-89701-968-3 (summary of human responses to averting visible laser radiation (PDF; 120 kB).).