Coherence (physics)

In physics, coherence (from Latin : cohaerere = to be connected) denotes the property of an extended wave field that the momentary deflections at different locations change over time in the same way except for a constant phase shift . As a result, a spatially stationary interference can become visible when coherent waves are superimposed . The lack of coherence is known as incoherence .

While the often chosen mathematical description of a wave as a sinusoid is thought to be unlimited in time and space, real physical waves are limited in time and space. Also, two waves generated by different arrangements usually have slightly different frequencies. The presence of coherence therefore mostly indicates a common or coherent history of the origin of the waves. Depending on the duration of this formation, the coherence can be limited in time; the distance covered is called the coherence length , which measures the spatial extent of its coherence.

Coherence plays a role in all areas of physics in which interferences are observed, especially in laser optics, spectroscopy and interferometry . It makes no difference to the importance of coherence whether it is light waves or matter waves . Since it is possible, especially in laser technology , to generate numerous copies of individual photons with a coherent history of their origin, coherence is particularly important in their areas of application, such as the creation of holograms , quantum cryptography or signal processing .

The correlation integral serves as a measure of the interference ability of two waves and thus the coherence of the two .

More detailed description

All physical waves such as light waves, radar waves, sound waves or water waves can be coherent to other waves in a certain way, or there can be coherence between corresponding partial waves. The cause of the coherence can be a common history of the origin of the waves. If, for example, the same causal mechanism was the basis for the generation of the waves, constant vibration patterns can arise in the wave train, which can later be made visible by comparing partial waves. If the wave amplitudes of two waves are directly correlated with one another, this becomes evident when the waves are superimposed on the occurrence of stationary (spatially and temporally unchangeable) interference phenomena. In other cases, a technically higher effort or a more complicated mathematical consideration of the wave course is sometimes necessary in order to prove coherence in the waves.

In simple cases, such as with periodic waves, two partial waves are coherent if there is a fixed phase relationship to one another. In optics, this phase relationship often means a constant difference between the phases of the oscillation period. Partial waves, which are superimposed at a certain (time-averaged) intensity at a fixed location (e.g. on an observation screen), can then either intensify or extinguish (complete coherence), or slightly intensify or weaken (partial Coherence) or equalize to a medium intensity (incoherence) . In this case, incoherence is mainly present at different frequencies if all phase differences occur equally often and no constructive or destructive interference is possible as a result.

On the other hand, waves with different frequencies can also have coherence with one another. Technically, this type of coherence plays a role in the frequency comb or in radar technology . This coherence is generated by mode coupling or frequency doubling or multiplication.

In wave fields one can also differentiate between the cases of temporal and spatial coherence, even if both forms of coherence must normally be present. Temporal coherence exists when there is a fixed phase difference along the time axis (often figuratively equated with the spatial axis parallel to the direction of propagation). Spatial coherence exists when there is a fixed phase difference along a spatial axis (often reduced to the spatial axes perpendicular to the direction of propagation).

Mathematical representation

Coherence and correlation

The coherence in waves necessary for interference capability can be quantified using the correlation function. This function provides a measure of the similarity of the temporal progression of two related wave amplitudes.

The function

{\ displaystyle \ Gamma _ {\ mathrm {A} \ mathrm {B}} (\ tau) = \ langle E (\ mathbf {r} _ {\ mathrm {A}}, t) E ^ {*} (\ mathbf {r} _ {\ mathrm {B}}, t + \ tau) \ rangle = \ lim \ limits _ {T \ to \ infty} {\ frac {1} {T}} \ int \ limits _ {- T / 2} ^ {+ T / 2} {E (\ mathbf {r} _ {\ mathrm {A}}, t) E ^ {*} (\ mathbf {r} _ {\ mathrm {B}}, t + \ tau) {\ textrm {d}} t}}

first defines the (complex) cross-correlation function between the time courses of two observed amplitudes. The two amplitudes are picked out at the location points A and B of the wave and when there is a time difference of and compared as a function of time . ${\ displaystyle E}$ ${\ displaystyle \ tau}$ ${\ displaystyle t}$

The contrast function for spatiotemporal coherence, which by

{\ displaystyle K _ {\ mathrm {A} \ mathrm {B}} (\ tau) = \ left | {\ frac {2 \ Gamma _ {\ mathrm {A} \ mathrm {B}} (\ tau)} { \ Gamma _ {\ mathrm {A} \ mathrm {A}} (0) + \ Gamma _ {\ mathrm {B} \ mathrm {B}} (0)}} \ right |}

is given, now directly supplies the strength of the coherence as a value between 0 and 1. In general, one distinguishes three cases:

	${\ displaystyle K _ {\ mathrm {A} \ mathrm {B}} (\ tau)}$	= 1	complete coherence
0 <	${\ displaystyle K _ {\ mathrm {A} \ mathrm {B}} (\ tau)}$	<1	partial coherence
	${\ displaystyle K _ {\ mathrm {A} \ mathrm {B}} (\ tau)}$	= 0	complete inconsistency

In the case of purely temporal coherence, only correlations with A = B are considered. Here the contrast function provides temporal coherence

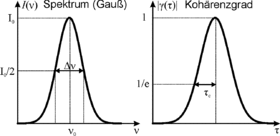
{\ displaystyle K (\ tau) = \ left | {\ frac {\ Gamma (\ tau)} {\ Gamma (0)}} \ right |}

the strength of the temporal coherence as a function of the time interval . has a maximum value of 1 and, depending on the coherence, falls more or less quickly to 0. The coherence time is defined as the time interval at which the contrast function has dropped to 1 / e. If the coherence between different waves is to be calculated, the cross-correlation function ${\ displaystyle \ tau}$ ${\ displaystyle K (\ tau)}$ ${\ displaystyle \ tau = 0}$ ${\ displaystyle \ tau _ {c}}$ ${\ displaystyle \ tau}$

{\ displaystyle \ Gamma (\ tau) = \ langle E_ {1} (t) E_ {2} ^ {*} (t + \ tau) \ rangle}

of waves and used. ${\ displaystyle E_ {1}}$ ${\ displaystyle E_ {2}}$

In the case of purely spatial coherence, only correlations are considered. Here the contrast function provides spatial coherence ${\ displaystyle \ tau = 0}$

{\ displaystyle K _ {\ mathrm {A} \ mathrm {B}} = \ left | {\ frac {2 \ Gamma _ {\ mathrm {A} \ mathrm {B}}} {\ Gamma _ {\ mathrm {A } \ mathrm {A}} + \ Gamma _ {\ mathrm {B} \ mathrm {B}}}} \ right |}

the strength of the spatial coherence between points A and B. A volume in which all pairs of points A, B have a contrast forms a so-called coherence volume , within which there is spatial coherence. Most of the time, the term spatial coherence is understood to mean only the coherence transverse to the direction of propagation of the wave, which would have to be referred to more precisely as transversal spatial coherence . The spatial coherence along the direction of propagation, i.e. the longitudinal spatial coherence , on the other hand, is often equated with the temporal coherence, which is only approximately correct. ${\ displaystyle K _ {\ mathrm {A} \ mathrm {B}}> 1 / e}$

Multi-beam interference

The mathematical definition of coherence shown only describes the correlation between two points on a wave. In many applications, however, the condition must be met that a large number of partial waves can overlap to form a common interference pattern. The pairwise coherence of the partial waves alone is not sufficient. For this purpose, the concept of coherence must be expanded or linked to additional conditions.

In the example of a diffraction grating in optics, for example, in which a very large number of partial waves must interfere, the paired spatial coherence is not sufficient to make sharp diffraction spectra visible. In addition, there must be a simultaneous correlation between the phases of all partial waves, so that the partial beams that are in pairs capable of interference come into congruence in a common diffraction maximum on the screen. This condition is met in particular when plane wave fronts hit a plane diffraction grating. Two other applications in which multi-beam interference plays a role are Bragg reflection and the Fabry-Pérot interferometer .

Consistency in classic optics

In classical optics, coherence is directly related to the ability of light to interfere. The contrast of the interference pattern V ( Visibility ) is a measure of the coherence of the light. In optics in particular, the two special cases of spatial and temporal coherence play a major role.

Coherence and Contrast of an Interferogram

In optics, coherence means the ability to interfere with a specific experiment and is associated with the contrast of the interference pattern, which can be a maximum of 1 (completely coherent light) and a minimum of 0 (completely incoherent light). The interference pattern of two light sources depends on their complex mutual coherence function or the complex mutual degree of coherence or on the contrast ${\ displaystyle V}$ ${\ displaystyle \ Gamma = \ left \ langle E_ {1} E_ {2} ^ {*} \ right \ rangle}$ ${\ displaystyle \ gamma = {\ frac {\ Gamma} {\ sqrt {I_ {1} I_ {2}}}}}$ ${\ displaystyle V = {\ frac {2 {\ sqrt {I_ {1} I_ {2}}}} {I_ {1} + I_ {2}}} \ left | \ gamma \ right |}$

{\ displaystyle I = I_ {1} + I_ {2} + 2Re \ {\ Gamma \} = I_ {1} + I_ {2} +2 {\ sqrt {I_ {1} I_ {2}}} Re \ {\ gamma \}}

For two-beam interference of a wave with its spatially and temporally shifted copy , the two-beam interference formula results . ${\ displaystyle E_ {1} = E ({\ vec {r}} _ {1}, t_ {1})}$ ${\ displaystyle E_ {2} = E ({\ vec {r}} _ {2}, t_ {2})}$ ${\ displaystyle I = I_ {0} \ left (1 + V \ cos (\ Delta \ Phi) \ right)}$

Temporal coherence

Interference between two temporally separated points of a wave

Light arises from discontinuous emission acts that send out photon wave trains. These wave trains are each connected to a regularly oscillating field that randomly changes its phase. "This interval in which the light wave represents a sinusoidal oscillation is a measure of its temporal coherence." The coherence time is thus defined by the mean time interval in which the light wave oscillates in a predictable manner. A higher coherence time corresponds to a higher temporal coherence of a light-emitting source.

Individual wave packets of the same frequency and different phase. The sum signal results in a coherence time in the order of magnitude that corresponds to the duration of the individual wave packets.

Temporal coherence is necessary if the wave is to be coherent with a time-shifted copy of itself. This is the case, for example, when the path lengths in a Michelson interferometer have different lengths in the object and reference arm. The time after which the relative values of phase and / or amplitude have changed significantly (so that the correlation decreases to a decisive extent) is called the coherence time . When the coherence is still not perfect, but it has on the time significantly reduced. The coherence length is defined as the distance that the wave travels within the coherence time. ${\ displaystyle \ tau _ {c}}$ ${\ displaystyle \ Delta t = 0}$ ${\ displaystyle \ Delta t = \ tau _ {c}}$ ${\ displaystyle l_ {c}}$

Wiener-Chinchin theorem

In the case of a light source, the temporal coherence is determined by the spectral composition of the light. Light from a monochromatic light source is completely coherent in time. Light that is composed of different wavelengths (e.g. due to Doppler broadening ) is - depending on the type of composition - partially coherent or incoherent. This relationship is described by the Wiener-Chintschin theorem , which states that the degree of coherence (as an autocorrelation function of the field strength) corresponds to the normalized Fourier transformation of the light spectrum. The coherence length of light is defined as the point at which the degree of coherence has dropped to. ${\ displaystyle 1 / e}$

The connection between the spectrum of the light source and the temporal coherence can be illustrated using the Michelson interferometer as an example. When the reference mirror is tilted, the path length difference between the two beams is linearly dependent on the tilting direction. If the path length difference corresponds to an integral multiple of the wavelength, the rays interfere constructively and the interference pattern has a maximum. With monochromatic light, a striped pattern is visible on the screen.

If the light has different wavelengths, the individual stripe patterns are shifted to one another. The greater the wavelength, the wider the stripes. When the stripe patterns are superimposed on a viewing screen, the stripes cancel each other out or reinforce each other (partial coherence) in some places. The return of the contrast cannot be explained in the picture of the finitely long wave trains.

Temporal coherence as a Fourier transform of the spectrum of the light source

If one calculates the coherence function according to the Wiener-Chintschin theorem for the case of a laser with a Gaussian spectrum (bandwidth FWHM = , centroid wavelength ), one obtains a Gaussian coherence function with the coherence length . ${\ displaystyle \ Delta \ lambda}$ ${\ displaystyle \ lambda}$ ${\ displaystyle l_ {c} = {\ frac {\ lambda ^ {2}} {\ Delta \ lambda}}}$

From the Fourier transformation it follows directly that - depending on the shape of the spectrum (for example not in the above case of the Gaussian spectrum, but for example for a beat in which the autocorrelation function is periodic) - also for greater path length differences than again a high coherence can be achieved. This property of coherence cannot be explained in the clear picture of the finitely long wave trains (see below). ${\ displaystyle l_ {c}}$

Clear explanation of the temporal coherence through finite wave trains

“Natural” light is created when an electron in an atom changes from an excited to a less excited state. When the excited state decays, the electron oscillates for a certain time in the semiclassical conception. During this time (= lifetime) it will emit a photon (damped oscillation ). Typical lifetimes of such atomic processes are (= coherence time). This leads to wave packets with lengths of (= coherence length ) with a frequency uncertainty of about 100 MHz. ${\ displaystyle \ tau = 10 \, \ mathrm {ns}}$ ${\ displaystyle l_ {c} = c \ tau \ approx 3 \, \ mathrm {m}}$ ${\ displaystyle \ Delta f = {\ frac {1} {\ tau}}}$

The resulting light is made up of wave packets that were emitted by many different atoms and differ in phase and frequency. Since the atoms are mostly in thermal motion, the light emitted by such atoms shows Doppler broadening , and with strong mutual interaction (e.g. collisions) of the atoms also pressure broadening . Both effects shorten the coherence time or length of the emitted light considerably.

Modeling the decays using finite wave trains cannot explain all aspects of temporal coherence, but it serves as an aid in simple cases.

Spatial coherence

Interference between two points along a wave

If the wave is to interfere with a spatially shifted copy of itself, spatial coherence is necessary. This is the case , for example, in Young's double slit experiment : Here, two points are picked out from the incident wave by the two slits and brought to interference. The extent of the area of spatial coherence describes how far apart these two points may be.

Van-Cittert-Zernike theorem

Complex degree of coherence as a Fourier transform of the intensity distribution of the light source for a round light source

In the case of an extended light source with a statistical phase distribution, i. H. Applicable to LEDs, light bulbs and gas discharge lamps, but not to lasers, the spatial coherence is determined by the size and shape of the light source. It is more about the angular extent than the actual extent, so that the spatial coherence therefore increases with increasing distance. A point light source has complete spatial coherence even at a short distance. This relationship is described by the Van-Cittert-Zernike theorem - after Pieter Hendrik van Cittert (1889–1959) and Frits Zernike - which states that the complex degree of coherence of the standardized Fourier transform corresponds to the intensity distribution of the light source (conditions: small dimensions of the Light source and the observation area, sufficient observation distance). For a circular light source, the spatial coherence drops rapidly and reaches its minimum depending on the distance between the observation screen and the light source. After that, the coherence is not lost, but comes back for larger distances (in a very weak form). ${\ displaystyle 1 {,} 22 \ lambda z / 2 \ rho}$ ${\ displaystyle z}$

The relationship between the expansion of the light source and spatial coherence can be illustrated using the example of the double-slit interference experiment. An interference pattern is created on the observation screen depending on the difference in transit time between the two beams. A sufficiently high temporal coherence of the light beams is necessary for this. For the point of the observation screen that lies between the two columns, the light rays have no transit time difference. Here the interference pattern has the zeroth maximum. In the case of an extended light source, the point with a transit time difference of zero is slightly shifted for each point of the light source. The individual interference patterns blur each other depending on the size of the light source.

Generation of coherent light

The choice of light source is crucial for coherence. However, coherence is not a property of a light source itself, but of the light rays, since the light's ability to interfere can be lost during propagation.

If one sends spatially non-coherent light through a very narrow gap, the light behind it behaves as if the gap were a point light source (in one dimension) that emits elementary waves (see Huygens principle ). In the case of a simple gap, the size of the spatial coherence area is indirectly proportional to the gap size (van-Cittert-Zernike theorem, Verdet's coherence condition ). With increasing distance from the light source, the angular extent of the light source decreases and thus the spatial coherence increases.

The temporal coherence of the light can be increased by using a wavelength filter that limits the spectrum of the light source.

Fluorescent tubes, incandescent lamps and gas discharge lamps are spatially extended light sources (spatially incoherent) that produce white light of a large amount of different frequencies (temporally incoherent). Using pinhole diaphragms and wavelength filters, spatially and temporally coherent light can be generated, but the remaining intensity of the light is greatly reduced so that this method is not very practical.

Laser light, on the other hand, is considered to be the most easily generated monochromatic light and has the greatest coherence length (up to several kilometers). For example, a helium-neon laser can produce light with coherence lengths of over 1 km. However, not all lasers are monochromatic (e.g. a titanium: sapphire laser can also have spectral widths of Δλ ≈ 2 - 70 nm). LEDs are less monochromatic (Δλ ≈ 30 nm) and therefore have shorter coherence times than most monochromatic lasers. Since a laser usually has the same phase over its entire exit aperture, the emitted laser light also has a very high spatial coherence.

Measurement of coherence

Temporal coherence

The coherence time or coherence length of a light wave can be determined by dividing it into two partial beams and combining them again later - for example in a Michelson interferometer or Mach-Zehnder interferometer . One sees interference phenomena in such an arrangement only when the difference in transit time or the path difference between the partial waves remains smaller than the coherence time or coherence length of the wave trains emitted by the atoms.

The time coherence can also be determined from the measurement of the spectrum by means of Fourier transformation. Conversely, the spectrum of a light source can also be determined by measuring the interference contrast in a Michelson interferometer while the path length difference is varied ( FTIR spectrometer ).

Spatial coherence

Similar to the case of temporal coherence, spatial coherence can be determined by measuring the contrast of an interference pattern if an interferometer is used that is sensitive to spatial coherence (relatives of the double-slit structure). In stellar interferometry, the angular extent of stars is determined by measuring the contrast using spatial coherence.

swell

↑ The mathematical definition follows the textbook Coherent Optics by Werner Lauterborn . The * marks the transition to the complex conjugated.
↑ Eugene Hecht: Optics . 4th, revised edition. 2005, p. 631 .

literature

Paul, Harry: Lexicon of Optics . Spectrum Academic Publishing House, 2003, ISBN 3-8274-1422-9 .
Lauterborn, Werner : Coherent Optics. Basics for physicists and engineers . Springer 1993, ISBN 3-540-56769-0 .
Lipson; Lipson; Tannhauser: optics . Springer 1997, ISBN 3-540-61912-7 .
Goodman, Joseph: Statistical Optics . Wiley 1985, ISBN 0-471-01502-4 .
Roy J. Glauber : Quantum Theory of Optical Coherence: Selected Papers and Lectures. Wiley-VCH, Weinheim 2007, ISBN 978-3-527-40687-6 .

Web links

Commons : Coherence - collection of images, videos and audio files

[1] The mathematical definition follows the textbook Coherent Optics by Werner Lauterborn . The * marks the transition to the complex conjugated.

[2] Eugene Hecht: Optics . 4th, revised edition. 2005, p. 631 .