Phase shift

The phase shift , also called phase difference or phase position , is a term used in physics and technology in connection with periodic processes. Two sinusoidal oscillations are mutually shifted in their phase angles if their period durations match, but the times of their zero crossings do not. A constant phase shift can also be specified if the period lengths are not the same, but are integral multiples of each other.

Phase shifts can occur where timers, inertia or reactances play a role, especially in electrical engineering , electroacoustics , acoustics and vibration mechanics . The term is also used in other areas, see below .

Right: Two oscillations in their course over the phase angle , which are mutually shifted by the angle . Left: Two rotating hands with the same difference in phase angle. Their projections onto the vertical straight line through the origin result in the instantaneous values. The oscillation drawn in blue precedes the oscillation drawn in red by 60 °. ${\displaystyle \omega t}$ ${\displaystyle \Delta \varphi }$

illustration

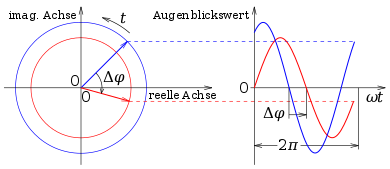
A phase shift can be seen in a line diagram of the alternating quantities over time at the offset of the zero crossings (with the same sign of the slopes of the curves). It can also be illustrated in the pointer model . The two oscillations are symbolized by pointers, which both rotate around the coordinate origin with the same constant angular velocity . A pointer is a complex quantity with the real part and the imaginary part . The horizontal deflection and the vertical deflection are both real, see also DIN 1302 . ${\displaystyle \omega }$ ${\displaystyle {\underline {z}}}$ ${\displaystyle {\underline {z}}=x+\mathrm {j} y}$ ${\displaystyle \mathrm {Re} \,{\underline {z}}=x}$ ${\displaystyle \mathrm {Im} \,{\underline {z}}=y}$ ${\displaystyle x}$ ${\displaystyle y}$

A full revolution corresponds to a full period of the oscillation. The phase shift angle , also referred to as phase rotation , is here the angle enclosed by the two pointers.

The sense of direction of the phase shift of an oscillation compared to the reference oscillation leads to the terms lag angle or lead angle , further lag or lead. The use of the pointers as complex quantities makes mathematical calculations much easier (see complex AC calculation ).

Size of the phase shift

Motor nameplate with details of cos  φ to identify the phase shift (right in the middle)

A period corresponds to the full angle of 360 °, and the phase shift over time is specified as an angle . Instead , it is also written simply , provided that confusion is impossible. An indexed formula symbol is more unambiguous; for example, an explanatory note can be used for the difference in a voltage versus a current intensity . The same applies to the spelling together with . ${\displaystyle \Delta \varphi }$ ${\displaystyle \Delta \varphi }$ ${\displaystyle \varphi }$ ${\displaystyle u={\hat {u}}\,\sin(\omega t+\varphi _{u})}$ ${\displaystyle i={\hat {\imath }}\,\sin(\omega t+\varphi _{i})}$ ${\displaystyle \varphi _{u}-\varphi _{i}}$ ${\displaystyle \varphi _{ui}}$ ${\displaystyle \varphi _{ui}}$ ${\displaystyle u={\hat {u}}\,\cos(\omega t+\varphi _{u})}$ ${\displaystyle i={\hat {\imath }}\,\cos(\omega t+\varphi _{i})}$

Angles are given in radians or degrees ; z. B. the information and 90 ° mean the same phase shift of a quarter period. It is also possible to specify the phase shift time as a measure or a length specification if a spatial distance is covered during the process, e.g. B. with a light beam. ${\displaystyle {\frac {\pi }{2}}}$ ${\displaystyle \Delta t=\Delta \varphi /\omega }$

In electrical power engineering, the phase shift is indicated by the cosine of the phase shift angle , that is. The " ", also known as the active factor , is specified on every AC motor rating plate and other reactive electrical loads and is used, for example, to calculate the active power share of the total output or to dimension switch contacts (see switching arc ). (The sole specification of does not say anything about the "type" or flow direction of the reactive power (whether inductive or capacitive reactive power consumption), since the sign of is lost when the is formed.) ${\displaystyle \varphi }$ ${\displaystyle \cos \varphi }$ ${\displaystyle \cos \varphi }$ ${\displaystyle \cos \varphi }$ ${\displaystyle \cos }$ ${\displaystyle \varphi }$

With an oscilloscope , two or more oscillations that are shifted in time can be made immediately visible as individual curves in their time course. The time offset of the zero crossings and the period can be read off and the phase shift angle calculated: ${\displaystyle \Delta t}$ ${\displaystyle T}$

${\displaystyle {\frac {\Delta \varphi }{360^{\circ }}}={\frac {\Delta t}{T}}\;.}$

If the phase angles match, ie if the phase difference is zero, the oscillations are referred to as "in-phase" or "in-phase"; colloquially they are "in phase".

Manifestations, applications

Electrical engineering

Phase shift between current and voltage at an inductance

Phase shift between current and voltage on a capacitance

Three-phase alternating voltage consists of three alternating voltages, each oscillating 120 ° from one another

In electrical engineering, the term phase shift in an AC circuit is used in connection with currents and voltages. A shift always occurs when a two-port operated with alternating current has inductive or capacitive, differentiating or delaying properties. In the high frequency range, the signal propagation time alone can be responsible for this.

Phase shift between complex voltage and complex current ${\displaystyle {\underline {u}}(t)}$ ${\displaystyle {\underline {i}}(t)}$

• With an inductance (ideal coil ) the current strength follows the voltage by 90 ° (the voltage leads the current strength by 90 °). The phase shift angle is given as positive; it is independent of the frequency. ${\displaystyle \Delta \varphi =\varphi _{ui}}$
• With a capacitance (ideal capacitor ), the voltage follows the current strength by 90 °. The phase shift angle is given as negative; it is independent of the frequency.
• With ohmic resistance , voltage and current are always in phase.
• With a combination of R, L and C , the phase shift angle can assume any value between −90 ° and + 90 °; it depends on the frequency and changes particularly strongly in the vicinity of a resonance point ; compare: resonant circuit .

See also : Impedance  and Electrical Resistance # AC Resistance

High frequency technology

Here the phase shift is used for phase modulation . In the two-sided frequency spectrum, this means that the pointer of the signal frequency points in alternating directions in relation to the pointer of the carrier frequency. This can be used to encode data.

Acoustics, sound engineering

Phase-shifted sinusoidal oscillations of the same frequency

If two or more sound waves of the same frequency are superimposed, an either amplified or attenuated signal results depending on the phase shift angle. Such an overlay is called interference and is location-dependent in the sound field: depending on the distance and position of the sources, all possible combinations of amplifications and attenuations result at different observer positions (on the subject of attenuation, see also anti-noise ).

${\displaystyle \Delta \varphi }$	${\displaystyle \Delta \varphi }$	${\displaystyle f}$	${\displaystyle \lambda }$
360 °	2 π rad	2000 Hz	0.1715 m
180 °	π rad	1000 Hz	0.3430 m
90 °	π / 2 rad	500 Hz	0.6860 m
45 °	π / 4 rad	250 Hz	1.372 m
22.5 °	π / 8 rad	125 Hz	2,744 m
11.25 °	π / 16 rad	62.5 Hz	5.488 m

With the definition of the units for the plane angle

${\displaystyle 1\ \mathrm {rad} =1\ {\frac {\mathrm {m} }{\mathrm {m} }}=1\;;\quad 1^{\circ }=(\pi /180)\ \mathrm {rad} }$,

with the wavelength and the speed of sound  = 343 m / s at 20 ° C ${\displaystyle \lambda =c/f}$ ${\displaystyle c}$

For example, for a fixed delay of = 0.5 ms, the adjacent frequency-dependent phase shift angle results : ${\displaystyle \Delta t}$ ${\displaystyle \Delta \varphi }$

The unit radian can be omitted if it is not intended to clarify an angle.

For the acoustic connection between phase shift and time difference in stereophony, see time stereophony . With digital signal processing it is now possible to adjust the phase position of signals fed to several loudspeakers individually and thus to control the sound field specifically for a small listening point or measuring point. ${\displaystyle \Delta \varphi }$ ${\displaystyle \Delta t}$

other areas

In the optical lenses are antireflection coated by a thin layer on the glass surface a double reflection created which at a certain wavelength λ , a phase shift of the two reflections of ½  λ achieved. The layer thickness is usually set to the wavelength of the yellow light ( λ ≈ 600 nm).

Schematic representation of the pig cycle

Phase shifts are also known in economics , such as B. the pig cycle . Time delays in the regulating mechanism between demand , supply and the resulting price as well as the investment incentives derived from them explain the phenomenon of a phase shift between price and flow of goods.

In ecology , periodic population fluctuations are often observed in predator-prey relationships . The predator population fluctuates with respect to the prey population with a phase delay. (see Lotka-Volterra rules )

In the case of thermal insulation , phase shift describes the period between the occurrence of the highest temperature on the outer surface of a component until the highest temperature is reached on its inner surface, although there is no sinusoidal function.

Mathematical description

Equations for vibration and rotating pointer

→ Main article : Complex AC bill

The simplest case of an oscillation is the harmonic oscillation. Mathematically it can be described by

${\displaystyle x(t)={\hat {x}}\cdot \cos(\omega \cdot t+\varphi _{0})\;;\quad {\underline {x}}(t)={\hat {x}}\cdot \mathrm {e} ^{\mathrm {j} (\omega \cdot t+\varphi _{0})}}$

where the real value at the time , the complex value, the amplitude, the angular frequency , the frequency and the imaginary unit represent. is called the phase angle and the zero phase angle . ${\displaystyle x(t)}$ ${\displaystyle t}$ ${\displaystyle {\underline {x}}(t)}$ ${\displaystyle {\hat {x}}}$ ${\displaystyle \omega =2\pi f}$ ${\displaystyle f}$ ${\displaystyle \mathrm {j} }$ ${\displaystyle \varphi (t)=\omega \,t+\varphi _{0}}$ ${\displaystyle \varphi _{0}}$

Phase shift angle and phase delay

The relationship between the phase shift angle and the transit time difference is: ${\displaystyle \Delta \varphi }$ ${\displaystyle \Delta t}$

${\displaystyle \Delta \varphi =\omega \cdot \Delta t=2\pi \cdot f\cdot \Delta t}$

or moved

${\displaystyle \Delta t={\frac {\Delta \varphi }{\omega }}={\frac {\Delta \varphi }{2\pi \,f}}={\frac {\Delta \varphi }{360^{\circ }\,f}}}$

based on the conversions given above

${\displaystyle \omega =2\pi f\ }$   and   . ${\displaystyle 2\pi =360^{\circ }}$

Phase shift by 180 ° and phase reversal

Sawtooth signal as an example of a non-symmetrical signal:
top: original signal,
middle: signal phase shifted by 180 ° in the basic
oscillation, bottom: signal with reverse polarity

In the event of a phase reversal , positive instantaneous values become negative and negative instantaneous values ​​become positive . In the case of a symmetrical, for example sinusoidal, alternating signal, a phase reversal appears like a phase shift by 180 ° of the fundamental oscillation. In general there is no relationship between phase shift and phase inversion.

Web links

Wiktionary: phase shift  - explanations of meanings, word origins, synonyms, translations

• Phase shift φ and transit time difference Δ t (PDF file; 178 kB)
• Calculator: Relationship between phase, phase angle, frequency and transit time (delay)
• Reverse polarity and phase shift are different terms (PDF; 62 kB)
• Calculate phase angle φ - The phase shift as a practical application with the oscilloscope (www.Afug-Info.de)

Individual evidence

1. ↑ ^{a b c} DIN 1311-1: 2000 Vibrations and systems capable of vibrating .
2. ↑ ^{a b} DIN 40 110-1: 1994 alternating currents - two-wire circuits .
3. ↑ ^{a b} DIN 1301-1: 2010 units - unit names, unit symbols .