Reactance
The reactance (also reactance ) is a quantity in electrical engineering which limits an alternating current by building up an alternating voltage and causes a temporal phase shift between voltage and current strength. The value of the reactance depends on the frequency. The addition of “blind” stems from the fact that electrical energy is transported to the reactances, but is not converted into thermal, mechanical or chemical energy there.
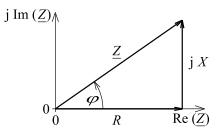
Reactance in the complex AC calculation
The reactance is a physically existing real variable for processes in alternating current technology. A mathematical treatment of sinusoidal processes is possible with trigonometric functions, but it is often laborious. To make it easier, the calculation can be carried out in a mathematically elegant manner with complex quantities, with the results then having to be converted into real quantities.
In the complex AC calculation, the reactance is the imaginary part of the complex resistance ( impedance ). The real part of is called the effective resistance . The Pythagorean sum of real and reactance is called impedance . The instantaneous values of voltage and current are also complex quantities in this calculation .
The unit of the reactance is - as with the effective resistance - the ohm with the unit symbol Ω.
In general:
From this it follows for the reactance:
- For
or
- For
Inductive and capacitive reactance
Capacitors and coils are energy stores. When electricity flows, a capacitor creates an electric field ; when a voltage is applied to a coil, it builds up a magnetic field . During this time, electrical energy is withdrawn from a current or voltage source . However, this energy can be returned to the source when the current or voltage direction is reversed - unlike with an effective resistance. The course of energy transport is determined by the course of the voltage or current.
The most frequently observed curve in electrical engineering is that of sinusoidal alternating quantities. In this case, the energy storage device is charged and discharged periodically through a sinusoidal voltage curve and a phase-shifted sinusoidal current curve (" reactive current "). The relationship between the voltage and the current, which is shifted by a quarter period , is called reactance, and the energy oscillating between the source and the energy storage device is called reactive energy .
In the case of a transient, one-time charging or discharging process, the curve of the absorbed or released energy follows an exponential function . These time courses can be determined in particular by solving differential equations .
Reactance with sinusoidal signals
The derivation of the following equations can be found under the keywords complex alternating current calculation and electrical resistance .
Kitchen sink
For an ideal coil with the inductance is its impedance
where j is the imaginary unit.
Their reactance, also called inductance , is the imaginary part of the impedance:
Their reactance is a linear alternating current resistance (independent of voltage or current strength), which increases with increasing frequency (or increasing angular frequency ). A calculation example of the inductive resistance is here to see.
capacitor
For an ideal capacitor with capacitance is its impedance
Its reactance, historically also known as capacitance , is the imaginary part of the impedance:
- Note on the convention
- This notation corresponds to international standards. In the literature, the amount of the capacitive reactance is sometimes referred to as. Then the amounts from and from each other are deducted in common formulas . In the convention used here (see also impedance , series resonant circuit ), the capacitive reactance is negative in contrast to the inductive reactance . Physically, the opposite sign means the opposite phase position between voltage and current.
The reactance of an ideal capacitor is also a linear alternating current resistance , but its magnitude decreases with increasing frequency .
Reactance with non-sinusoidal signals
If the voltage or current curve is not sinusoidal, no clear reactance can be specified. Every periodic signal can be represented by a sum of sinusoidal signals of different frequencies, which is the basis of Fourier analysis . These harmonics , which occur in addition to the sinusoidal fundamental oscillation, must each be taken into account and their reactance values determined. A single reactance value cannot be specified; instead, a superimposition of different reactances at different frequencies and different voltage or current amplitudes has to be determined. The current curve is thus distorted compared to the voltage curve. This case occurs, for example, with non-linear loads, such as switched-mode power supplies , or with inductive components that are in magnetic saturation .
Reactance of an electrical consumer on the power grid
An ideal linear reactance only causes reactive power in the network , but does not consume any real power . The electrical energy required to build up and break down electric or magnetic fields is returned to the generator, but puts a strain on the lines.
Reactive resistances, however, never occur on their own, since in practice there are no lossless circuits. Reactive resistances are always linked to real resistances that actually convert power.
If the inductive reactance predominates over the capacitive one in a consumer, the consumer is referred to as ohmic-inductive, otherwise as ohmic-capacitive.
Example : The series choke in fluorescent and gas discharge lamps is an inductive series resistor (reactance) for current limitation and therefore causes only small losses (ohmic and magnetic losses) compared to an ohmic resistance .
The following consumers are usually ohmic-inductive:
- Electric motors
- Transformers
- Fluorescent and gas discharge lamps with conventional ballast , if not compensated
- Sagittarius
The following consumers are usually ohmic-capacitive:
- Switching power supplies without power factor correction (engl .: P ower F actor C orrection, PFC), u. a. many computer power supplies
- Capacitor power supplies
- Frequency converter without PFC
- Fluorescent lamps with a series connection of a choke and capacitor (used for reactive current compensation of other luminaires without this series connection)
- Capacitors for reactive power compensation (stand-alone control cabinets or part of lights and other inductive loads)
The first two capacitive consumers mentioned are - if they do not have any circuit measures for power factor correction - also non-linear loads due to the input rectifier; In addition to reactive power, they therefore also generate harmonics in the supply network.
See also
Web links
Individual evidence
- ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: International Electrotechnical Dictionary Entry 131-12-46
- ↑ EN 80000-6: 2008, quantities and units - Part 6: Electromagnetism ; Entry 6-51.3