Reactive power

Reactive power is a term used in electrical engineering . In the electrical energy supply network , energy should be transmitted from the generator to the consumer. In networks operated with single-phase or three-phase alternating current (three-phase current), more energy often flows between the generator (power plant) and an electrical consumer (e.g. electrical machine ) than is converted in the consumer in the same number of periods . This additional energy per time that does not contribute anything to the active power ("actual power") is referred to as reactive power. It is largely undesirable.

Determinations

The article uses the consumer counting arrow system, which is widely used in electrical engineering , to determine the direction .

In the case of equal quantities , the electrical power is defined from voltage and current strength . ${\displaystyle P=U\cdot I}$ ${\displaystyle U}$ ${\displaystyle I}$

In alternating quantities , according to the instantaneous value of the power of the instantaneous values of the voltage and the current strength defined. Instead of the instantaneous values, if possible, values ​​obtained through averaging (integration) and constant in stationary processes are used: ${\displaystyle p=u\cdot i}$ ${\displaystyle u}$ ${\displaystyle i}$

• the rms values of voltage and current ${\displaystyle U={\sqrt {\,{\overline {u^{2}}}\;}}}$ ${\displaystyle I={\sqrt {\,{\overline {i^{2}}}\;}}}$
• three performance figures
  • the real power ${\displaystyle P={\overline {\,p\,}}={\overline {u\;i\,}}}$
  • the apparent power ${\displaystyle S=U\cdot I}$
  • the total reactive power ${\displaystyle Q_{\mathrm {tot} }={\sqrt {S^{2}-P^{2}}}}$

These definitions apply generally according to standardization.

The unit of power is the watt ( symbol W). In electrical power engineering, according to the same standards - also in DIN 1301-2 ("units") - the volt-ampere (unit symbol VA) and for reactive power the var (unit symbol var) are mainly used for apparent power ; applies here . ${\displaystyle 1\mathrm {var} =1\mathrm {VA} =1\mathrm {W} }$

Further specifications in DIN 40108 and DIN 40110-2 must be observed for the supply network.

Sinusoidal voltages and currents

Shift reactive power

For use in the power supply network, and are alternating quantities with the same basic frequency . If they are also both sinusoidal with and , possibly shifted by the phase shift angle , as well as with the amplitudes and , according to the derivation of the active power applies ${\displaystyle u}$ ${\displaystyle i}$ ${\displaystyle u={\hat {u}}\sin \omega t}$ ${\displaystyle i={\hat {\imath }}\sin(\omega t-\varphi )}$ ${\displaystyle \varphi }$ ${\displaystyle {\hat {u}}={\sqrt {2}}\;U}$ ${\displaystyle {\hat {\imath }}={\sqrt {2}}\;I}$

${\displaystyle P=U\;I\ \cos \varphi }$ .

The phase shift creates a shift reactive power . To derive it, the current strength is broken down using an addition theorem into ${\displaystyle i}$

Instantaneous values ​​of the power
The power consumed by the consumer (curve 1) is made up of a component that contributes to the real power (curve 3) and a remainder that contributes to the reactive power (curve 2)

${\displaystyle i={\hat {\imath }}\sin(\omega t-\varphi )={\hat {\imath }}\sin \omega t\cos \varphi -{\hat {\imath }}\cos \omega t\sin \varphi }$ .

This represents an active current strength that corresponds to the voltage in terms of the phase angle and a reactive current strength that is offset by 90 °. This is the instantaneous value of the performance ${\displaystyle u}$

${\displaystyle p=u\,i={\hat {u}}\,{\hat {\imath }}\sin ^{2}\omega t\cos \varphi -{\hat {u}}\,{\hat {\imath }}\sin \omega t\cos \omega t\sin \varphi }$

and with the double angle functions

${\displaystyle p={\frac {1}{2}}{\hat {u}}\,{\hat {\imath }}\cos \varphi \cdot (1-\cos 2\omega t)-{\frac {1}{2}}{\hat {u}}\,{\hat {\imath }}\sin \varphi \cdot \sin 2\omega t}$ .

This equation is broken down in the diagram opposite. Curve 2 shows the second summand as an oscillation around height zero, which therefore does not contribute anything to the energy flow on average over time . The factor in this summand is used in analogy to the definition of the active power to define the displacement reactive power ${\displaystyle {\tfrac {1}{2}}{\hat {u}}\,{\hat {\imath }}\sin \varphi }$ ${\displaystyle Q}$

${\displaystyle Q={\frac {1}{2}}{\hat {u}}\,{\hat {\imath }}\sin \varphi =U\;I\ \sin \varphi }$ .

The total reactive power with sinus curves results from the definition above

${\displaystyle Q_{\mathrm {tot} }={\sqrt {S^{2}-P^{2}}}=U\;I\,{\sqrt {1-\cos ^{2}\varphi }}=U\;I\,|{\sin \varphi }|}$ .

If no confusion is possible, the reactive power shift alone is called reactive power . ${\displaystyle |Q|=Q_{\text{tot }}}$

The two possible signs of characterize two types of phase-shifting passive two-pole devices (consumers): ${\displaystyle Q}$

Inductive consumer: The current lags behind the voltage	${\displaystyle 0^{\circ }<\varphi <90^{\circ }}$	${\displaystyle Q>0}$
Capacitive consumer: The current strength precedes the voltage	${\displaystyle 0^{\circ }>\varphi >-90^{\circ }}$	${\displaystyle Q<0}$

In electrical engineering, it is common to carry out the alternating current calculation (i.e. calculating with sinusoidal alternating quantities) with the help of pointers in the complex plane , since this is much simpler than the calculation with trigonometric functions . Then in the complex AC calculation, the reactive power is the imaginary part of the complex electrical power .

The following section was inserted after a discussion that was controversial to the end; it is not yet part of the article.

This is a call for third opinions that have been missing so far.

See discussion: Reactive Power # Phase Shift Angle at the end of the long chapter.

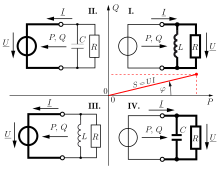
Signs of power and ranges of the phase shift angle of active two-pole devices

Signs of active and reactive power in the four quadrants of the phase shift angle with circuit examples ${\displaystyle -180^{\circ }<\varphi \leq 180^{\circ }}$

The passive two-poles that have only been considered up to now (see table above) occupy quadrants I and IV in a - diagram (see graphic on the right) . Active bipoles can have an inductive or capacitive effect. Whether they draw or supply reactive power is determined solely by the connected passive two-pole: If a - -bipole is connected (quadrant II), the active two-pole picks up the reactive power generated by the - -bipole and thus acts inductively. If a - bipole is connected (quadrant III), the active bipole that supplies the reactive power has a capacitive effect. The signs of the - and values ​​and the value range for all possible load cases can be seen in the - diagram . A correctly placed simple circuit is drawn as an example in each of the four quadrants . With respect to their reactive power the thickly drawn (ie after the act consumer convention bepfeilten) Two poles in the upper half plane inductively and capacitively those in the bottom. With regard to their active power, they act as a motor in the right half-plane and as a generator in the left . ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle \tan \varphi =Q/P}$ ${\displaystyle -90^{\circ }<\varphi <90^{\circ }}$ ${\displaystyle R}$ ${\displaystyle C}$ ${\displaystyle R}$ ${\displaystyle C}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle {\mbox{Q-}}}$ ${\displaystyle \varphi }$ ${\displaystyle \varphi }$

root cause

Time curve of voltage , current strength and power with a purely ohmic consumer ${\displaystyle u}$ ${\displaystyle i}$ ${\displaystyle p}$

Time curve of voltage , amperage and power with a purely inductive consumer ${\displaystyle u}$ ${\displaystyle i}$ ${\displaystyle p}$

With an ohmic load , the voltage and current have an in-phase curve, which is the phase shift angle . All of the energy supplied by the producer is converted by the consumer (e.g. as thermal or chemical energy). ${\displaystyle \varphi =0}$

In the case of an inductive consumer (e.g. choke coil , transformer , asynchronous motor ), the energy supplied by the generator is used to build up the magnetic field . The energy is initially stored in the magnetic field, but with the periodic change in the sign of the voltage, the field is reduced again and the energy is fed back into the network. With a purely inductive load, the current follows the voltage by a quarter of a period, the phase shift angle is 90 °. The product is off and is alternately in the positive and negative range, with the frequency of the power being twice the fundamental frequency. If the power is in the negative range, it means that energy is being returned to the grid. The power fluctuates around its mean level of zero, which shows that energy in the network only oscillates back and forth. However, it generates a “blind” flow of electricity . In this case it results ${\displaystyle u}$ ${\displaystyle i}$ ${\displaystyle p}$

${\displaystyle Q=U\cdot I\cdot 1=S\,;\quad P=0}$

The same applies to capacitive loads (e.g. capacitor motors , underground cables ), which, however, generate an electric field instead of the magnetic one that sets a phase shift in the other direction, but otherwise delivers the same thing: the one for building up and reducing the field pro Period of energy transported represents reactive power.

To clarify: Active power stands for energy consumption at which electrical energy is drawn and mostly irreversibly converted into another form of energy. Displacement reactive power, on the other hand, stands for energy demand at which electrical energy is drawn, stored for a fraction of a network period and then reversibly fed back into the network.

The reactive power usually occurs in all components connected to the network and also in the line network itself. Since, in principle, the three passive linear properties of capacitance , inductance and ohmic resistance are always present in a circuit , either in discrete components or as a " line covering ", there is practically always a reactive power load in an AC supply network.

Reactive power load

Overview of the occurrence of reactive power

Reactive power occurs in the following areas:

• inevitable due to inductive or capacitive loads connected to the power grid and the grid itself (see section above)
• targeted by setting the excitation current in synchronous machines in power plants for central reactive power compensation, setting the grid voltage and load flow control
• through targeted decentralized reactive power demand in order to
  • to compensate decentrally required reactive power or
  • to influence the voltage at the grid connection point

Example for the last point: According to VDE AR-N-4105, photovoltaic inverters with an apparent power of 13.8 kVA or more also respond in the standard setting at full load with inductive reactive power demand , because this lowers the voltage at the feed point. This is intended to counteract the increase in the line voltage at the feed point due to the ohmic resistance and thus enable a higher power to be fed in before the inverter would have to be disconnected from the grid at a line voltage of 253 V. ${\displaystyle \cos \varphi =0{,}9}$

consequences

The power is drawn from the supply network when the voltage and current have the same sign. If the signs are opposite, the power is fed back again. The feedback causes a reactive power and a reactive current , which increases with increasing reactive power demand of the consumers. To counteract the heating of the line, larger conductor cross-sections in the supply lines as well as larger generators and transformers are required. Large electrical consumers in industry have to pay not only for the active energy they use, but also for their reactive energy. Private and small consumers, who, in contrast to industry, mainly purchase electricity for heat generation, cause low reactive power load and are therefore exempt from the costs due to the high effort involved in recording them, or the costs can be found in the price of the real work (specified in kWh) again. - In addition, reactive load changes cause significantly greater voltage changes in the network, since the internal resistance of generators and transformers is predominantly inductive. ${\displaystyle p}$

Example of reactive power

Due to the small distance between the cores, underground cables represent a large capacitive load for a given length. The approximately 11.5 km long 380 kV Berlin Transversal has a capacity of 2.2 μF. To reload this at 50 Hz, a reactive current of 160 A must be applied, which corresponds to a reactive power of 110 Mvar. This is why the maximum sensible cable length is limited to around 70 km.

Countermeasures

The large energy consumers try to keep the reactive power requirement as low as possible by taking suitable measures. The inductive reactive power requirement of an asynchronous machine can be compensated by a capacitor battery , synchronous machine or a special converter ( power factor correction ), this is called reactive power compensation . The energy required to generate the magnetic field then no longer shuttles into the supply network to the generator, but only between the asynchronous machine and capacitor bank or synchronous machine. This reduces the resulting current that the drive draws from the network. The top picture illustrates this in the three curves shown:

Curve 1: power consumed by the machine; it oscillates with the amplitude  . ${\displaystyle S}$

Curve 2: Power to be delivered by the capacitor; it oscillates with the amplitude  . ${\displaystyle |Q|}$

Curve 3: Then power drawn from the grid; it oscillates with the amplitude  . ${\displaystyle |P|}$

For drives with asynchronous machines, the reactive power requirement is defined by the motor and largely independent of the mechanical drive power. Compensation with the help of a capacitor battery, synchronous machine or a special converter (power factor correction) is possible. In systems with a variable reactive power requirement, it is necessary that a regulated compensator is used instead of a compensation device with constant reactive power (capacitor).

The reactive power within a regional power grid can be compensated by phase shifting transformers or rotating phase shifters .

The parallel connection of capacitance and inductance for this purpose can also be viewed as an oscillating circuit which, with a suitable design, has its resonance frequency at 50 Hz and blocks reactive current. An example is shown under reactive power compensation .

Non-sinusoidal currents

With sinusoidal voltage, non-sinusoidal currents can also occur. This is the case with all non-linear consumers, such as converters in power electronics or with inductors that saturate magnetically . Non-sinusoidal currents can also occur in power supplies without power factor correction . See also current flow angle .

Such a current is a sum of sinusoidal components of different frequencies; In addition to the fundamental component, it also contains harmonic components . If the rms value of the fundamental oscillation is designated with , ... the rms values ​​of the harmonics, then applies to the active power ${\displaystyle I_{1}}$ ${\displaystyle I_{2}}$ ${\displaystyle I_{3}}$

${\displaystyle P=U\;I_{1}\;\cos \varphi _{1};}$

only the parameters of the fundamental oscillation of the current are important; Harmonics have no influence. In contrast, all harmonics are included in the result for apparent and reactive power. ${\displaystyle P}$

${\displaystyle S=U\;I=U\;{\sqrt {I_{1}^{2}+I_{2}^{2}+I_{3}^{2}+\dotsc }}}$

With the total reactive power

${\displaystyle Q_{\mathrm {tot} }={\sqrt {S^{2}-P^{2}}}\ ,}$

a displacement reactive power in the fundamental

${\displaystyle Q_{1}=U\;I_{1}\ \sin \varphi _{1}}$

and a distortion reactive power in the harmonics

${\displaystyle Q_{d}=U\;{\sqrt {I_{2}^{2}+I_{3}^{2}+\dotsc }}}$

surrendered

${\displaystyle Q_{\mathrm {tot} }={\sqrt {Q_{1}^{2}+Q_{d}^{2}}}\ .}$

Reactive power meters, insofar as they work like real power meters as described below, only record (with sinusoidal voltage) . Electronic devices with sufficiently fast digital sampling and calculation also allow the measurement of . ${\displaystyle Q_{1}\,}$ ${\displaystyle Q_{\mathrm {tot} }}$

Multiphase system

In the cause section in the first picture you can see that with sinusoidal voltage and ohmic load the instantaneous power does not have any negative instantaneous values, but fluctuates. So there is a mean value (the active power) and a power fluctuation, which in this case is not reactive power.

With the transition to the symmetrical three-phase system , the active power triples. Because there are no return conductors (only 3 instead of 6 conductors are required), the feed line losses only increase by a factor of 1.5. This saving in feed line losses can be explained by the fact that in the symmetrically loaded three-phase network the total power is constant over time, i.e. no power fluctuation occurs.

In the case of an asymmetrical load, additional losses occur in the neutral conductor; they are superimposed on the temporal course of the total power as oscillations. This effect is described with asymmetry reactive power .

Measurements in the energy supply network

This section is limited to the case that voltage and current are sinusoidal, but with a phase shift .

Measuring device

A power meter has a current path and a voltage path . It multiplies instantaneous values ​​of voltage and current strength, averages over the instantaneous values ​​of the product and is therefore an active power meter according to the definition of active power. Alternatively, the device is suitable for measuring reactive power if the voltage on the voltage path lags behind the voltage on the consumer by 90 °. For measuring devices that can only output positive values, the polarity of the voltage must be reversed in the case of a capacitive reactive load to avoid negative measured values.

If the voltages on the consumer and on the voltage path have the same rms value, measurement is made ${\displaystyle {\underline {U}}}$ ${\displaystyle {\underline {U}}_{\text{Spg.pfad}}}$

${\displaystyle {\overline {u_{\text{Spg.pfad}}\;i\;}}=U\;I\ \cos(\varphi -90^{\circ })=U\;I\ \sin \varphi =Q\ .}$

In a single-phase network, an artificial circuit is required for phase shifting, e.g. B. the Hummel circuit , which generates a shift of 90 ° with two lossy coils and an ohmic resistor at a fixed frequency.

Voltage vector for the three-phase network in the complex plane

Reactive power measurement in a single-phase network

Voltages shifted by 90 ° - voltages rotated by 90 ° in the pointer representation in the complex plane - are directly available in the undistorted three-phase network with neutral conductor. For example, is lagging by 90 °  . However, the voltages are different in the amount:  . Using a series resistor or a voltage converter , however, the voltage can be reduced by the factor ; Depending on the circumstances, the result can also be corrected mathematically. ${\displaystyle {\underline {U}}_{3\mathrm {N} }}$ ${\displaystyle {\underline {U}}_{12}}$ ${\displaystyle U_{12}={\sqrt {3}}\ U_{3\mathrm {N} }}$ ${\displaystyle 1/{\sqrt {3}}}$

For the measurement with the correct sign, it is important to ensure that the paths are correctly connected, which are specified by correct circuit diagrams. The existing standardization for the normal case is consistently applied within this article in the circuit diagrams. How the insertion of a measuring device into the circuit is shown on the basis of the circuit diagram, how the display is transferred to the circuit using the identification of the path terminals, what is to be observed with the measuring device, is explained under the keyword active power measurement . ${\displaystyle |\varphi |<90^{\circ }}$

Single-phase network

The usual circuit corresponds to the circuit for real power measurement, only that the current through the voltage path has to be shifted by 90 ° compared to the voltage, - as a rule as stated above: voltage on the voltage path lagging by 90 ° compared to the voltage on the consumer.

Three-phase network

Four-wire circuit with neutral wire

Reactive power measurement in a three-phase network

The most comprehensive case is the four-wire circuit with a neutral conductor and three outer conductors, as is common in the low-voltage network with = 230 V or = 400 V, in connection with any load. Arbitrary means here: Currents with different amplitudes and different phase shift angles can flow in the three outer conductors with respect to the respective reference voltage. This means that the reactive power can be measured with three power meters or a combination device. The corresponding circuit for measuring inductive reactive power is shown in the picture. What should be measured, namely ${\displaystyle U_{1\mathrm {N} }}$ ${\displaystyle U_{12}}$

${\displaystyle Q=U_{1\mathrm {N} }\;I_{1}\sin \varphi _{1}+U_{2\mathrm {N} }\;I_{2}\sin \varphi _{2}+U_{3\mathrm {N} }\;I_{3}\sin \varphi _{3}\ ,}$

is measurable with the voltages lagging by 90 ° as

${\displaystyle Q={\frac {1}{\sqrt {3}}}\left({\overline {u_{23}\;i_{1}}}+{\overline {u_{31}\;i_{2}}}+{\overline {u_{12}\;i_{3}}}\right).}$

Three-wire circuit

Aron circuit; above for active power measurement, below for reactive power measurement

Due to the lack of a neutral conductor in the three-wire circuit

${\displaystyle i_{1}+i_{2}+i_{3}=0.}$

As shown in the article on active power, a current can be deducted here , and two power meters in Aron circuit are sufficient. The corresponding picture shows the measuring circuits for active and reactive power. Both are suitable for any load. The calculation for the active power results ${\displaystyle i_{2}}$

Current and voltage phasors in the undistorted voltage triangle, originally and lagging by 90 °

${\displaystyle P={\overline {u_{12}\;i_{1}}}+{\overline {u_{32}\;i_{3}}}.}$

To connect the voltages lagging by 90 °, the neutral conductor potential in the three-wire circuit must be artificially created through a star point as shown in the figure with a resistance that is just as large as the resistance of the voltage path in the power meters. Since the rotated voltages are smaller by the factor here , the measured values ​​must be increased by the factor (with a voltage converter or by calculation), and this results ${\displaystyle 1/{\sqrt {3}}}$ ${\displaystyle {\sqrt {3}}}$

${\displaystyle Q={\sqrt {3}}\cdot ({\overline {u_{\mathrm {N} 3}\;i_{1}}}+{\overline {u_{1\mathrm {N} }\;i_{3}}})}$

${\displaystyle Q={\sqrt {3}}\cdot \left(U_{\mathrm {N} 3}\;I_{1}\ \cos \delta _{1}+U_{1\mathrm {N} }\;I_{3}\ \cos \delta _{3}\right)}$

where = angle between and ${\displaystyle \delta _{1}=60^{\circ }-\varphi _{1}}$ ${\displaystyle {\underline {U}}_{\mathrm {N} 3}}$ ${\displaystyle {\underline {I}}_{1}}$

and = angle between and . ${\displaystyle \delta _{3}=120^{\circ }-\varphi _{3}}$ ${\displaystyle {\underline {U}}_{1\mathrm {N} }}$ ${\displaystyle {\underline {I}}_{3}}$

The individual measured values ​​of the two measuring devices have no clear meaning, not even in the sign. If it becomes smaller than 30 °, the second summand becomes negative; a correct connection is required for measuring with the correct sign. ${\displaystyle \varphi _{3}}$

Symmetrical loading

With symmetrical loading, it is sufficient to use only one power meter for the power consumption through one of the outer conductors. The total output is three times that.

${\displaystyle Q=3\cdot U_{1\mathrm {N} }\;I_{1}\;\sin \varphi _{1}.}$

This becomes with the twisted tension

${\displaystyle Q={\sqrt {3}}\cdot U_{23}\;I_{1}\;\cos \gamma _{1}}$

where = angle between and ${\displaystyle \gamma _{1}=90^{\circ }-\varphi _{1}}$ ${\displaystyle {\underline {U}}_{\mathrm {2} 3}}$ ${\displaystyle {\underline {I}}_{1}.}$

See also

• Reactance
• Blind work
• complex ac bill
• Asynchronous generator
• Double-fed asynchronous machine

literature

• Réne Flosdorff, Günther Hilgarth: Electrical energy distribution. 4th edition, Teubner, Stuttgart 1982, ISBN 3-519-36411-5 .
• Horst Bumiller u. a. (Ed.): Electrical engineering. 29th edition, Europa-Lehrmittel, Haan-Gruiten 2014, ISBN 978-3-8085-3190-7 .
• Horst Stöcker (Ed.): Pocket book of physics. 6th edition, Harri Deutsch, Frankfurt am Main 2010, ISBN 978-3-8171-1861-8 ; 7th edition. Europa-Lehrmittel, Haan-Gruiten 2014, ISBN 978-3-8085-5677-1
• Günter Springer: Electrical engineering arithmetic book. 11th improved edition, Europa-Lehrmittel, Haan-Gruiten 1992, ISBN 3-8085-3371-4 .

Web links

Wiktionary: reactive power  - explanations of meanings, word origins, synonyms, translations

• AC basics
• Ballast in power lines: the reactive power

Individual evidence

1. ↑ ^{a b c} DIN 40110-1: 1994 AC quantities, section 3.3.1
2. ↑ ^{a b} DIN EN 80000–6: 2008 Sizes and units - Part 6: Electromagnetism , Sections 6.56 ff
3. ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: Internationales Electrotechnical Dictionary - IEV. , Entry 131-11-44
4. ^ Wilfried Weißgerber: Electrical engineering for engineers 2: alternating current technology, locus curves, transformers, multi-phase systems . Vieweg, 6th ed., 2007, p. 146
5. ↑ Wolfgang Böge, Wilfried Plaßmann (ed.): Vieweg Handbook Electrical Engineering: Fundamentals and applications for electrical engineers. Vieweg, 4th ed., 2007, p. 312
6. ↑ DIN 40110-1: 1994 alternating current quantities, Sections 2.3 and 3.3.1
7. ↑ Beckhoff: Signs for power measurement. Beckhoff, accessed on July 29, 2020 . 
8. ↑ Energy portal: four-quadrant counter. Energy portal, accessed on August 4, 2020 . 
9. ↑ From an RWE publication, quoted in: Herbert Niederhausen, Andreas Burkert: Electric power: production, transmission, distribution, storage and use of electrical energy in the context of the energy transition. Springer Vieweg, 2014, p. 389
10. ↑ Dayo Oshinubi: Energy-efficient evaluation electronics for capacitive micromechanical yaw rate sensors. KIT Scientific Publishing, 2010, p. 51
11. ↑ Volkmar Seidel: Start-up electrical engineering. Teubner, 2000, p. 96 f
12. ↑ SMA: SMA basic knowledge of reactive power. SMA, accessed July 18, 2018 .