Phase angle

This article covers the phase angle in physics and engineering; for meaning in astronomy see day-night boundary

Physical size
Surname	Phase angle, phase
Formula symbol	${\displaystyle \varphi }$
Size and unit system unit dimension SI wheel 1

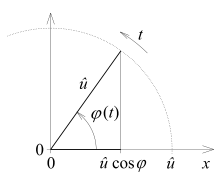
The phase angle or phase indicates the current position in the course of a periodic process. For sinusoidal curves, the phase is the quantity on which the angle function depends directly (mathematically referred to as the “argument” of the function ). It therefore has the dimension of an angle.

Pointer of length û rotating with constant angular frequency ω  . The phase angle φ ( t ) increases linearly with time. The projection of the pointer onto the x -axis is û  cos φ .

The course of a harmonic oscillation can be visualized by a pointer that rotates around the origin of the coordinates at a constant angular velocity (see illustration). If you project this pointer onto one of the two coordinate axes, the end point of the projection carries out the harmonic oscillation. The angle that the pointer makes with the horizontal axis is the phase angle.

Definitions

For the cosine function

${\displaystyle x(t)={\hat {x}}\,\cos(\omega t+\varphi _{0})}$

the following quantities are defined in the standards:

• the phase angle as the linear time dependent argument of this function, ${\displaystyle \varphi (t)=\omega t+\varphi _{0}}$
• the angular frequency as a constant with the frequency or the period , ${\displaystyle \omega =2\pi f=2\pi /T}$ ${\displaystyle f}$  ${\displaystyle T}$
• the zero phase angle as the phase angle at the point in time . ${\displaystyle \varphi _{0}\ }$ ${\displaystyle t=0}$

This is coupled with two sinusoidal oscillations of the same frequency

• the phase shift angle as the difference between the phase angle or zero phase angle of the two oscillations. This variable is sometimes also referred to as “phase difference”, “phase difference” or “phase shift”. Unlike the phase angle, the phase shift angle is a constant over time. ${\displaystyle \Delta \varphi }$
  

Applications

• Electrical engineering :
  • In the case of alternating current resistors , alternating voltage and alternating current are phase shifted from one another.
  • With three-phase current , the voltage oscillations in the three lines are shifted by 120 ° each.
• Interference : When two or more waves are superposed , the current phase angle of all waves involved must be taken into account. If the waves are in phase at the point under consideration, they interfere constructively. Two waves in phase opposition of the same amplitude cancel each other out (destructive interference).
• Phase modulation : Targeted influencing of the phase angle for modulating a carrier in communications technology.

Individual evidence

1. ↑ DIN 1311-1 (2000): Vibrations and vibratory systems .
2. ↑ DIN 5483-1 (1983): Time-dependent quantities
3. ↑ DIN 40110-1 (1994): AC quantities