Impedance
The impedance ( lat. Impedire " hemmen ", "hinder"), also alternating current resistance , is an electrical resistance in alternating current technology . In the case of a two-pole network element, it indicates the ratio of electrical voltage to current strength . The term is used in particular when there is a phase shift between the two quantities , which means that the ratio of resistance differs in DC applications.
The impedance is a physical quantity used to describe it
- the behavior of a component or device (more precisely a passive linear two-pole ) when an electrical alternating current is applied (see also complex alternating current calculation ),
- the electromagnetic wave propagation in a line or a medium (see also wave impedance ). When the wave propagates, no specific component is involved in this resistance, neither an active nor a reactance .
General
The impedance is advantageously specified as a complex-valued function of the frequency . It is the summary of two statements:
- the ratio of the amplitudes of sinusoidal alternating voltage to sinusoidal alternating current and
- the shift in the phase angle between these two quantities.
Both properties are mathematically summarized by representing the impedance as a complex quantity:
- , where is the imaginary unit .
The amount of the complex impedance is the impedance . The time shift is given by the phase shift angle, which can assume values between −90 ° and + 90 °. In a different spelling is
The real part is the part of the impedance at which no phase shift occurs; this is always positive. The imaginary part is the part in which a phase shift of 90 ° occurs; this can be positive or negative, - positive when the current lags the voltage, - negative when the voltage lags the current. The phase-shifting component is frequency-dependent, the non-phase-shifting component can either be frequency-dependent or independent; see under keyword electrical resistance .
The reciprocal of the impedance is the admittance (complex conductance).
The choice of terms in this article follows the standardization which defines:
| Impedance (complex impedance) | ||
| Impedance, amount of impedance |
In the technical literature, the term impedance is not always used consistently and is used synonymously for both the complex size and its amount .
calculation
| R i | R a |
|---|---|
| Internal resistance | External resistance |
| Source resistance | Load resistance |
| Output resistance | Input resistance |
| Wave impedance | Terminating resistor |
The impedance is the quotient of the instantaneous values of complex alternating voltage and complex alternating current (for the representation of an alternating quantity as a complex alternating quantity see complex alternating current calculation ).
The impedance results as a quotient from the real amplitudes or from the effective values of the alternating voltage and the alternating current
In the case of the effective values, the normalizing factors are reduced.
In the case of electromagnetic wave impedance, voltage and current strength are replaced by other, corresponding quantities: the voltage through the field strength and the current strength through the magnetic flux density and in acoustics the voltage through the sound pressure and the current strength through the sound velocity .
Applications
The impedance is important for the adaptation of high frequency lines, but also for the wave propagation in free space. If, for example, the input impedance of a device does not match the impedance of the line, reflections occur , which reduces the power transmission and can lead to resonance phenomena and thus to a non-linear frequency response .
Electrodynamic loudspeakers are operated with alternating current, which is why the inductive resistance of the built-in voice coil causes a phase shift between current and voltage that is frequency-dependent. For this reason, we do not speak of resistance, but of the impedance of the loudspeaker.
If impulses are transmitted through cables , an ohmic resistance of the cable has little relation to the impedance of the cable. Here it is almost always important to avoid reflections of the impulses at the opposite end of the cable. The terminating resistor required for this is practically real for lossless lines, i.e. an ohmic resistor. This value is a characteristic impedance and characteristic impedance referred to the cable. Depending on the line losses at low frequencies, this can become complex-valued and highly frequency-dependent. It can be determined using time domain reflectometry .
In biology , the impedance can be used by means of electric cell substrate impedance sensing to detect changes in shape in animal cells . In the case of in vitro cell cultures, the electrical impedance at a fixed frequency is given as the TEER value .
The electrochemical impedance spectroscopy is an important method of investigation of the electrochemistry , both in basic research as well as various optimization electrochemical applications (. Eg energy storage such as batteries or fuel cells , electrochemical sensors such. As oxygen probes) is used.
presentation
The impedance has the unit ohm with the symbol Ω. In the two representations as a complex quantity , its components and their meaning can be read:
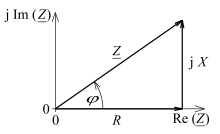
- When formulated in polar coordinates , the absolute value of the complex quantity stands for the impedance; it gives the length of the pointer in the vector diagram. The angle specification stands for the phase shift between voltage and current strength; In the vector diagram it results in the rotation of the pointer with respect to the real axis:
- When formulated in Cartesian coordinates , the real part stands for the effective resistance (resistance) or ohmic resistance , which converts the transmitted effective power . The imaginary part is the reactance (reactance) , which converts any real power, but saves energy and after a quarter period feeds back to the generator (see Reactive Power ):
In a consumer with an inductance , this has a positive (inductive) reactance ; the voltage leads the current. It stands for the angular frequency of the oscillation. In a consumer with a capacitance , however, this has a negative (capacitive) reactance ; the voltage lags the current. (For the sign convention used, see note under reactance , for derivation see under Complex AC Calculation ).
The vector diagram for shows how the component behaves,
- inductive: pointer in the first (upper right) quadrant of the coordinate system, positive imaginary part, or
- capacitive: pointer in the fourth (bottom right) quadrants, negative imaginary part .
The apparent resistance is provided by the Pythagorean addition of the active and reactive resistances:
In the case of technical devices, often only this amount of impedance, i.e. the apparent resistance, is specified. In a general network of ohmic resistances, inductances and capacitances, however, this is frequency-dependent.
Loudspeakers have highly frequency-dependent impedances - however, a nominal value (e.g. 4 Ω or 8 Ω) is specified. According to the international standard (IEC 60268), the lowest impedance occurring in the frequency range must not fall below this nominal value by more than 20%. Any higher impedances at other frequencies are permitted.
In high frequency - cables , the (maximum design) Characteristic impedance is referred to as characteristic impedance. It is 50 Ω to 100 Ω for coaxial cables and 110 Ω to 300 Ω for symmetrical (two-wire) lines.
In antennas , the input impedance is also called base impedance, it should at the frequency for which the antenna is intended to be real and match the impedance of the cable (eg., 60 Ω or 240 Ω).
Impedance matching
- See also: Reflection in electrical lines , impedance matching and wave impedance
When transmitting alternating voltage, waves are reflected when the impedance of a line or of the transmission medium changes. In principle, this is not tied to the number of wavelengths on a line, but with short transmission paths in relation to the wavelength, the change in the impedance of the transmission medium has hardly any effect. A part of the incoming wave is reflected at the place where the impedance changes. The magnitude of the reflection factor is between 0 and 1. If its magnitude is 1, the entire wave is reflected and if = 0 (that means ) there is no reflection, in this case impedance matching is present. This is often desirable with high-frequency lines and electromagnetic wave propagation.
literature
- Jürgen Detlefsen, Uwe Siart: Basics of high frequency technology. 2nd expanded edition. Oldenbourg, Munich a. a. 2006, ISBN 3-486-57866-9 .
- Adolf J. Schwab : electrical energy systems. Generation, transport, transmission and distribution of electrical energy. Springer, Berlin a. a. 2006, ISBN 3-540-29664-6 .
- Wolfgang-Josef Tenbusch: Basics of the loudspeakers. Michael E. Brieden Verlag, Oberhausen 1989, ISBN 3-9801851-0-9 ( Klang Ton Edition , 1).
- Gert Hagmann: Fundamentals of electrical engineering. 15th edition. AULA publishing house. Wiebelsheim, ISBN 978-3-89104-747-7
Web links
Individual evidence
- ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: International Electrotechnical Dictionary Entry 131-12-43.
- ↑ DIN 1304-1, symbols , 1994
- ↑ DIN 5483-3, time-dependent quantities, complex representation of sinusoidal time-dependent quantities , 1994
- ↑ DIN 40110-1, alternating current quantities ; Two-wire circuits , 1994
- ^ Ralf Kories, Heinz Schmidt-Walter: Taschenbuch der Elektrotechnik . 6th edition. Harri Deutsch, 2004, ISBN 3-8171-1734-5 , pp. 123 .