Wave resistance
The wave resistance , also the wave impedance or the impedance , is a property of a medium in which a wave propagates. The ratio of reflected and transmitted amplitude of the wave at an interface is determined by the wave resistance of the two media.
Electromagnetic waves in a homogeneous medium or in a vacuum
Field wave resistance
In electrodynamics is wave impedance - English wave impedance - the ratio between the electric and magnetic field component a is transversal propagating electromagnetic wave in a homogeneous, isotropic medium. The field wave resistance is formed from the square root of the quotient, which is composed of the generally complex permeability μ, the generally complex permittivity ε and the electrical conductivity σ. It is generally a complex quantity. For the material through which the wave moves, one obtains the field wave resistance with the imaginary unit j :
Here ω denotes the angular frequency . If the wave propagates in electrically non- conductive material, i. H. for σ = 0, the frequency dependence does not apply and the following applies:
In a vacuum, i.e. for , as well as , the field wave resistance results solely from natural constants. The free space wave resistance, i.e. the field wave resistance for an electromagnetic wave in a vacuum, is thus also a natural constant. Its value is real and amounts to
- .
For air ( ε r ≈ 1,00059) the wave resistance differs only slightly from this value. It is approximately .
The field wave resistance must not be confused with the line wave resistance known from line theory (see below).
Current and voltage waves on lines
Line impedance
The line impedance (also called cable impedance or nominal impedance , English characteristic impedance ) is a parameter of longitudinally homogeneous lines; these include B. cables or single wire assemblies consisting of at least two electrical conductors. The wave impedance of a waveguide is not considered here. The line impedance describes the ratio of current and voltage waves propagating in a common direction. In an electrical line, the line wave resistance Z l and the field wave resistance Z w are linked to one another via the geometry of the line boundary.
While the signal propagation behavior on a homogeneous line section is not determined by the wave impedance but by the propagation constant, its abrupt change (at joints) or any mismatches present at the line ends influence the signal propagation behavior - through reflection and refraction . This is particularly the case when the transmitted signals are high-frequency or contain high-frequency components. High is here compared to the reciprocal of the signal propagation time on the line; that is, in addition to the signal frequency, the cable length must be considered. This is e.g. B. the case for
- high frequencies (e.g. high frequency signals or steep- edged signals on practically any lines)
- long lines, such as B. Intercontinental 50 Hz high voltage lines
- Switching operations on lines (see pulse schedule )
The line impedance of homogeneous high-frequency lines is often a real quantity (e.g. 50 Ω for common coaxial cables) and is independent of the line length, but is usually slightly frequency-dependent ( dispersion ). The frequency dependence is essentially caused by non-ideal properties of the dielectric in the cable and must be taken into account for broadband signal transmissions. The line impedance should not be confused with the ohmic line resistance, which describes the (heat) losses when a current flows through the line. A clear idea of the line impedance is the input resistance of an endlessly long, homogeneous line, i.e. a line at the end of which no signal reflection takes place.
The line impedance, the line termination and the input impedance of a line
The line impedance does not exist in the sense of a component. Although an infinitely long line shows its wave impedance as input impedance at its beginning, in the real world the wave impedance is expediently specified by the manufacturer or calculated based on the geometry, since it cannot be easily measured. If, on the other hand, a line is terminated with a (possibly complex) resistor , the resistance value of which is the same as the wave resistance of the line, the line shows this resistance value at the beginning, regardless of its length. This case is called closed with the wave impedance: At the end of the line a resistor component or another load with the resistance value of the line wave impedance is connected. This can be an ohmic resistor or, for example, an antenna. However, this adaptation is only possible with a real load resistance if the wave resistance in the transmitted frequency range can also be assumed to be real. This is practically always the case with HF cables , for example .
If the line is not terminated with its characteristic impedance, the input impedance of the line generally varies depending on the line length, operating frequency, terminating impedance and line impedance and is complex. The matching of the impedances of the source, load and line impedance is only necessary if disturbing reflections or echoes of signals in both directions have to be avoided (example: bidirectional data cables such as USB ). Then the output has been matched, so the efficiency cannot be greater than 50%. If a higher degree of efficiency is required, it is sufficient to terminate the line without reflection (i.e. adapted) at the end - the signal source can have any source impedance. In the case of powerful transmitters, a different, usually much smaller source impedance is therefore always selected in order to enable a higher degree of efficiency - the Wachenbrunn transmitter achieved an efficiency of 85% in this way.
A distinction is made between the following three cases in high-frequency technology, of which the first two are often used to implement complex, frequency-dependent components such as resonant circuits , trap circuits or high-pass filters . Such components are called line circuits .

|
Representation of a coaxial line running open at the end. Incoming voltage pulses are reflected in phase, current pulses in opposite phase. At the end of the line, the total current from the outgoing and returning wave I = 0 is established. |

|
Representation of a coaxial line short-circuited at the end. Incoming voltage pulses are reflected out of phase, current pulses with the same phase. At the end of the line, the total current from the outgoing and returning current wave I = 2 · I (outgoing wave) is established . |
|
Representation of a coaxial line terminated with an impedance or a reflection-free with its line impedance. Incoming current or voltage pulses are not reflected if the terminating resistor has the value of the line impedance. For other values, the ratio between the outgoing and returning waves corresponds to the reflection factor . |
The line termination for voltage pulses
If a voltage pulse is applied to a homogeneous line that is not terminated with the characteristic impedance at the output, a reflection occurs at the location of the terminating impedance - comparable to an acoustic echo . As a result of the mismatch , a voltage-current ratio that differs from the line impedance is enforced, which causes the partial reflection of the incoming wave. The reflected pulse portion depends on the degree of mismatch. It runs counter to the incoming voltage pulse. If the source impedance of the signal source does not correspond to the characteristic impedance of the line, the signal is also reflected at the source impedance as an echo. The impulse then runs back and forth several times until its energy is converted into heat (see also time domain reflectometry ).
A line terminated with its wave impedance (right picture) prevents the reflection of voltage pulses as long as the impedance at the line termination matches the line wave impedance over the entire frequency spectrum of the pulse.
Equivalent circuit diagram of an electrical line

Figure 1 shows the equivalent circuit diagram of a line section of infinitesimal length d x . The sizes contained therein are the coatings related to the length: The inductance coating L ' , the capacitance coating C' , the resistance coating R ' and the dissipation coating G' . For sinusoidal signals, the complex amplitudes of voltage U and current I on the line can be used to determine the two differential equations of the homogeneous line with this equivalent circuit:
( j is the imaginary unit here.)
In the following, the line impedance is defined with the abbreviation Z l from the solution of the differential equation system.
Definition of the line impedance for the general solution of the line equations
If one differentiates the above first line equation with regard to x and then substitutes the expression for d I / d x from the second equation, one obtains the following linear differential equation of the second order
which through an approach of form
can be solved. By inserting the approach and comparing the coefficients, γ can be determined:
Because of the quadratic equation that occurs here, γ can be used with both positive and negative signs . These two solutions for the approach can be superimposed linearly (provided with two constants). They give the so-called “general solution” for the voltage U at a distance x from the start of the line
with the coefficients a 1 and a 2 depending on the boundary conditions . The complex parameter γ is called the propagation constant or also the propagation constant. It generally depends on the frequency and only if the Heaviside condition is met for the line is its real part constant and the imaginary part linearly dependent on the frequency.
The current strength at point x of the line can be determined from the line equations:
Using the above general solution for the voltage curve U ( x , ω ) results in the current curve I ( x , ω ) along the line as a function of the frequency ω :
The parameter Z l occurring therein is called the line impedance :
A calculation of the line coverings according to the conductor geometry and insertion into the general form of the line wave resistance shows: The closer the conductors are to each other and the larger the conductor cross-section, the lower the line wave resistance.
Frequency dependence of the line impedance
The behavior of the characteristic impedance of a line with direct current , low and high signal frequencies is explained below. The diagrams in this section serve to illustrate the frequency response of the line impedance, which corresponds to the input impedance of a lossy, infinitely long line. They show the frequency dependencies described in the following subsections using the example of the line impedance of a real three-phase overhead line for 110 kV. The frequency behavior of the line impedance discussed below can be seen particularly well on the locus .
Behavior with direct current
With direct current (0 Hz) the two frequency-dependent terms and thus the imaginary parts disappear in the general formula of the line impedance. Therefore, the line impedance becomes large and real at the frequency 0 Hz.
Ideally, it would be infinite. Typical values are between 100 kΩ and a few 10 MΩ.
Behavior at low frequencies
- → For the significance of the wave resistance in energy technology, see: Natural performance

At low frequencies, it is mainly the capacitive coating that becomes noticeable, as its effect very quickly dominates the effect of the discharge coating and (especially in the case of cables) the effect of the inductance coating has not yet reached the order of magnitude of the line resistance coating. Then L ' and G' can be neglected as a first approximation, so that the characteristic impedance is in a narrow frequency range
amounts. The locus can then be approximated by a straight line with a slope of −45 °.
This case is important for low frequency transmission lines and telephone lines. The equation is z. It is also used, for example, to determine the resistance and capacitor values of the line termination (the hybrid circuit ) in analog telephones . If the values are chosen correctly, the imaginary parts generated by the line are compensated. In this way, the effect of the mismatches can be prevented even though it has a (smaller) characteristic impedance that differs from the load resistor.
Behavior at high and very high frequencies
At high frequencies , the ohmic resistance per unit length can be R ' , and the conductance per unit length G' compared with the frequency-dependent terms of the capacitive and inductive pad j.omega.C ' or jωL' of the line of secondary importance. Then in the general equation for the line impedance R ' and G' can be replaced by zero, and the fraction within the root can then be shortened by jω . The line impedance therefore results for high and very high frequencies approximately from capacitive and inductive line coating and thus corresponds to the impedance of an ideal lossless line:
At very high frequencies in the order of GHz, although R ′ increases due to the skin effect and G ′ due to the dielectric dissipation factor in a real line , the resistance coating R ′ and the discharge coating G ′ still have a subordinate effect on the line impedance.
The wave resistance of a lossless line can, however, also be somewhat frequency-dependent due to the dispersion (see there) of the insulating material ( dielectric ) used.
For the reasons mentioned, a constant, real line impedance can often be expected from frequencies greater than 20 kHz. This line impedance value, which is only dependent on the line geometry and the dielectric, is usually a few 10 Ω ( coaxial line, e.g. 50 ... 75 Ohm) to a few 100 Ω (two-wire line 150 ... 300 Ohm). It is important for all high-frequency signals and also for the transmission of steep impulses.
Line and field wave resistance of selected line shapes
In a line there is a line wave resistance and a field wave resistance at the same location. One characterizes a natural current-voltage ratio of a wave, the other characterizes the natural ratio between the electric and magnetic field components of an electromagnetic wave. The field impedance in a line depends only on the material, the line impedance on the material and the line geometry. Both values exist side by side at the same place in a line and generally assume completely different values, which, however, are related to one another via the geometry of the line boundary.
The line impedance can be calculated from the geometry of the conductor and the permittivity of its insulation. The line impedance of a coaxial conductor ( coaxial cable ) is at high frequencies under the assumption μ r = 1:
with the permittivity ε r of the insulation material and the wave resistance of the vacuum . The field wave resistance between the inner conductor and outer conductor of the same coaxial line is :
This field wave resistance applies to the transverse electromagnetic field within the insulation of the coaxial line. It is only material-dependent and independent of geometry. The line impedance is material-dependent and depends on the geometry of the conductor edge. It is linked to the field wave resistance via the geometry of the inner and outer conductors.
The following applies to the two-wire line or Lecher line :
or equivalent, but including μ r :
The field wave resistance takes on the same form as with the coaxial line, because it does not depend on the line geometry, but only on the insulation material. The relationship between Z w and Z l shows the following form of the above equation for the two-wire line:
Default values
Not only does the wave resistance of a line depend on the size and geometry of the cross-section and the materials used, but also other parameters, such as signal attenuation, the optimization of which is often more important. This results in standard values for the wave resistance.
For coaxial lines with a given D and variable d , the adjacent diagram shows the attenuation curves due to ohmic losses and the transmittable power (with a given field strength on the inner conductor). The horizontal axis indicates the wave resistance that is also established. The minimum of attenuation is 77 ohms. Coaxial television antenna or cable television lines have a wave impedance of 75 Ω. For polyethylene as a dielectric, the minimum damping due to ohmic losses is 51 ohms. Coaxial laboratory measuring lines usually have a characteristic impedance of 50 Ω.
Two-wire lines as antenna lines with a value of 240 Ω are also common in older radio reception systems. Two-wire lines, shielded or unshielded, twisted or routed in parallel, usually have line impedances in the order of 100 to 200 Ω. At a given frequency, the adaptation to other input impedance values takes place, for example with the aid of resonance transformers .
Measurement of wave impedance
Electrical line
The wave impedance (line wave resistance) can be determined by measuring the alternating current resistance of the open line Z 0 (capacitor) and the alternating current resistance of the short-circuited line Z k (inductance) and taking the geometric mean of both measured values. The line impedance Z l is then:
Instead of the designation Z l , the designation Z w (w for shaft) is often used. It should be pointed out once again that this often leads to confusion or to the erroneous equation of the two related but unequal quantities of line impedance and field impedance.
Alternatively, time domain measurement methods are available. Aids for the experimental verification are the pulse generator and oscilloscope , which are also contained in a time domain reflectometer (TDR).
In a third method, the L (with the short-circuited end) and C (with the open end) of a short length of cable are measured with an AC voltage bridge and the line impedance is calculated using the formula . This method only delivers a reliable result if the length of the cable section is much smaller than a quarter of the wavelength of the measurement frequency in the cable.
Acoustic waves in free space (sound waves)
In acoustics, the characteristic sound impedance corresponds to the field wave resistance in electrodynamics - provided that there are no limitations. In the far field , pressure and velocity are in phase, which is why the characteristic acoustic impedance is real-valued and can be calculated from the density ρ and the speed of sound c of the transmitted medium:
It is also called wave resistance - as an analogy to the electrical resistance R = U / I , since the voltage is related to the force, like the sound pressure, and the speed is related to a particle flow. Its derived SI unit is Ns / m³ or Pa · s / m or kg / (s · m²). In the near field, a residual phase angle between sound pressure and sound velocity is measured, which is why Z F is then a complex number.
| medium | Characteristic impedance in |
|---|---|
| hydrogen | 110 |
| air | 413.5 at 20 ° C |
| water | 1.48 x 10 6 at 0 ° C |
| mercury | 19.7 · 10 6 |
| tungsten | 104.2 · 10 6 |
Acoustic impedance in the vicinity of waveguides
As soon as the wave moves near a boundary made of a different material, the wave impedance changes at some distance from the boundary. The transition area is fluid and is on the order of a wavelength. Examples from high frequency technology and optics show that the waveguides do not have to be hollow. With evanescence and Goubau line , the direction of wave propagation is no longer straight, but appears curved.
Acoustic waves in the cylindrical tube
If the sound propagates in pipes , the wall inhibits the propagation of the sound, since the wave impedances at the interface usually differ greatly. Then you do not speak more of the acoustic field impedance , ignoring the effects of limitations, but by the acoustic flow impedance Z A . This results from the quotient of sound pressure p and sound flow q . If all particles of the transmission medium on a surface A have the same sound velocity (velocity) v, i. That is, if the rhythmic flow through the pipe cross-section A is in phase everywhere and there are no standing waves, the equation can be simplified
The derived SI unit is Pa · s / m³.
Acoustic waves with a variable cross-section

In the event that the sound is directed not through a cylinder but through a funnel, the above formula does not apply. The wave impedance changes with the cross-sectional area of the sound channel; this is called an impedance transformer. Horn loudspeakers , mouthpieces , trumpets and macrophones transform the sound pressure very effectively into the speed of sound in order to increase the volume significantly. A phonograph cannot produce a noticeable volume without a bell: the stylus moves the membrane of a pressure chamber loudspeaker, which would be much too quiet on its own. With electromagnetic waves, too, a horn antenna transforms the wave impedance of a waveguide to the field impedance Z w0 of the free space. Without this transformer, hardly any energy would be radiated; instead, a standing wave would form in the waveguide . ( see also Vivaldi antenna )
In brass instruments , the shape of the bell has a number of properties:
- Flat, narrow-gauge funnels emit relatively little sound energy to the ambient air , while at the same time more energy is reflected into the instrument. This supports the formation of the standing wave, which makes these instruments respond very easily.
- Instruments with wide-gauge funnels sound louder because the impedance transformation is more uniform. At the same time, this reduces the energy reflected to form the standing wave and the instrument is relatively difficult to respond.
The impedance transformation also works in the opposite direction: an ear trumpet , formerly called a sound beam catcher, can collect sound waves and concentrate them on the eardrum.
Reflections at interfaces
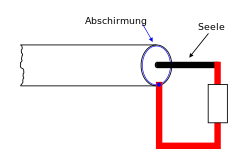
Sound is strongly reflected at the interface between two substances with a large difference in impedance. This difference is between air and z. B. water is particularly pronounced. Therefore, during an ultrasound examination, the probe is always coupled by means of a gel with a high water content, so that the sound is not reflected by air pockets between the probe head and the skin surface. In contrast, differences in impedance inside the body are desirable in order to obtain high-contrast images.
Illuminated objects can only be seen if light waves are reflected sufficiently strongly at an impedance difference. With glass doors this can lead to undesired collisions, with one-way mirrors , on the other hand, the reflectivity is increased by vapor-deposited layers in order to simulate opacity.
If the cross-section of a sound channel does not change slowly enough, the pipe end acts as a point of discontinuity that reflects part of the sound energy and allows it to run in the opposite direction. With certain pipe lengths there can be standing waves and as a result the acoustic flow impedance changes depending on the frequency by about a thousand times, as shown in the picture. This is the functional basis of all wind instruments . Strictly speaking, as in line theory , one has to calculate with complex numbers because of the phase shifts that occur. This is omitted here for the sake of clarity.
Acoustics: air-filled tube
If you measure the sound pressure and sound velocity at the end of a cylindrical pipe that is open on both sides with suitable microphones , you can calculate the flow impedance with the formula given the pipe cross-section
to calculate. Since both ends are open, this is the special case λ / 2 , which is well known when calculating electromagnetic waves along wires. The measurement result in the picture shows several sharp minima of the flux impedance at multiples of the frequency 500 Hz. A check with the pipe length of 325 mm and the speed of sound in air results in the target value 528 Hz.
The measured value of the deepest local minimum of the flow impedance is about 40,000 Pa · s / m³. Its product with the pipe cross-section results in 7 N · s / m³, which deviates considerably from the characteristic acoustic impedance of air (413.5 N · s / m³). There is therefore a mismatch which is greater the smaller the pipe diameter (D = 15 mm) compared to the wavelength. The vibrating column of air in the pipe is therefore only faintly audible here. It is the task of the tube expansions in wind instruments such as the trumpet to reduce this mismatch and thus increase the volume. A corresponding mismatch is also the cause of the very low efficiency of loudspeakers, which can be increased by a sufficiently large horn .
Reflections from changes in wave impedance
At the points where the wave resistance changes, there are reflections . The extreme cases of such changes in wave resistance are open and closed ends. The following analogies can be found:
| Type of wave | Open end | Closed end |
|---|---|---|
| Electromagn. Wave in the cable | not connected | shorted |
| Waveguide | ends open | conductively sealed |
| Vibrating rope / string | End hangs free | End is attached to a wall |
| Sound in the pipe | open end | Lid / stopper |
In the cases mentioned, there is almost complete reflection. The open waveguide, however, emits part of the electromagnetic wave. When a line is short-circuited, the voltage component of the reflected wave on a line changes its sign (also called phase jump or 180 ° phase shift ). In the case of an electromagnetic wave that hits a conductive layer perpendicularly, this is the case for the electric field component. The reflected wave then runs against the respective incident wave. Reflections (e.g. at the ends of a line) are the cause of standing waves .
Examples of weakened reflection
Acoustic wave
- A sound wave hits a soft cardboard box .
Electromagnetic wave
- Inhomogeneities in coaxial lines, v. a. Seamless change in wave resistance at connection points.
- Light hits a dirty pane of glass.
- Radar waves hit a cloud.
Mechanical shaft
- The end of a rope that is excited to vibrate is weighted with weights or attached to a fixed point with a spring.
- A wave of water meets tetrapods .
Examples of full reflection

- Acoustic wave
- A sound wave hits a hard wall from the air ( echo ).
Electromagnetic wave
- A coaxial cable is shorted or left open at the end.
- An electromagnetic wave hits an extensive, electrically ideally conductive surface (see radar cross-section ).
- Light hits a mirror.
Mechanical shaft
- A rope attached on one side is excited to vibrate.
- A wave of water hits a cliff coast .
Examples of anechoic closings
Complete freedom from reflection can only be achieved if the wave impedances on both sides of the interface match exactly. The lack of suitable materials can be compensated for by suitable shaping, as can be seen in the picture.
Acoustic wave
- Walls of an anechoic room . (Freedom from reflection through absorption )
- Bell horn of a gramophone . (Freedom from reflection through impedance matching to the characteristic sound impedance)
- Exponential funnel or horn and spherical wave horn on the horn (loudspeaker) .
Electromagnetic wave
- The source resistance of a transmitter corresponds to the line impedance of the cable (e.g. 50 Ω) and the input impedance of an antenna or equivalent load (see line matching ).
- Anti-reflective coating of optical components.
- A wave sump weakens the high-frequency wave in a waveguide by means of an absorbing material and only reflects a small proportion.
- Light hits a matt black surface.
- Mechanical shaft
- A water wave runs on a flat coast with a suitable angle of incline.
literature
- K. Küpfmüller and G. Kohn: Theoretical electrical engineering and electronics - An introduction . 16th edition. Springer, 2005, ISBN 3-540-20792-9 .
- Martin Gerhard Wegener: Modern radio reception technology . Franzis, 1985, ISBN 3-7723-7911-7 .
- Károly Simonyi: Theoretical electrical engineering . 10th edition. Barth Verlagsgesellschaft, 1993, ISBN 3-335-00375-6 , p. 545-671 .
- H.-G. Unger: Small textbook of electrical engineering . Volume IX: Theory of Lines. Friedr. Vieweg & Son, 1967.
Web links
- Electronics compendium - description of wave impedance
- Wave propagation on information technology lines
Individual evidence
- ↑ CODATA Recommended Values. NIST , accessed July 7, 2019 (value for the magnetic field constant).
- ↑ CODATA Recommended Values. NIST , accessed July 7, 2019 (value for the speed of light).
- ↑ Until the revision of the SI units in 2019 , the numerical values of the constants c and μ 0 were precisely defined by the definition of the units "meter" and "amperes". As a result, Z 0 expressed in SI units had the exact value 4π · 29.9792458 Ω.
- ^ Dieter Suter: Electronics. (PDF; 3.8 MB) (No longer available online.) Archived from the original on July 4, 2017 ; accessed on May 1, 2017 .
- ^ Karl Küpfmüller: Theoretical electrical engineering and electronics. 14th edition, Springer-Verlag, ISBN 3-540-56500-0 , pp. 453-496 (5th chapter: Lines and chain ladders ).
- ↑ Peter Vielhauer : Theory of transmission on electrical lines . Verlag Technik, Berlin 1970, DNB 458535036 .
- ↑ a b Sophocles J. Orfanidis: Electromagnetic Waves and Antennas , chap. 11.4.