Dispersion (physics)

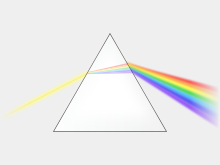
Dispersion in the prism creates a color spectrum

In physics , dispersion (from the Latin dispergere , “spread, disperse”) is the dependence of a physical quantity on the frequency of a wave . In optics this is specifically the speed of light propagation in media, which depends on the frequency of the light. It has the consequence that sunlight is refracted to different degrees on the surfaces of a prism . A colored spectrum therefore appears on the other side of the prism .

The relationship between the angular frequency (or the energy quanta ) of a harmonic wave and the wave vector is called the dispersion relation . In quantum theory in particular, this is the energy-momentum relationship of the particle .

Normal and abnormal dispersion

Refractive index of quartz glass depending on the wavelength (visible light to near infrared )

Influences of the addition of selected glass components on the optical dispersion of a special base glass.

In the case of most transparent materials, the refractive index increases with frequency in the visible range ; glass breaks blue light more strongly than red. One speaks of normal dispersion . A positive derivative of the refractive index according to the frequency of the wave ( ) is equivalent to a negative derivative according to the wavelength ( ). The following applies here with the speed of light in a vacuum and the phase speed . ${\ displaystyle n}$ ${\ displaystyle f}$ ${\ displaystyle {\ text {d}} n / {\ text {d}} f \,> \, 0}$ ${\ displaystyle \ lambda}$ ${\ displaystyle {\ text {d}} n / {\ text {d}} \ lambda \, <\, 0}$ ${\ displaystyle n = {\ tfrac {c} {v (\ lambda)}}}$ ${\ displaystyle c}$ ${\ displaystyle v (\ lambda)}$

On the other hand, if the refractive index falls with increasing frequency, then there is anomalous dispersion . It was discovered in an alcoholic fuchsine solution by Christian Christiansen in 1870. The effect is not a special property of this dye, rather it always occurs in wavelength ranges close to strong absorption . In general, the Kramers-Kronig relation links the course of the refractive index with that of absorption.

Quantitative description

A simple figure for the dispersion of an isotropic, transparent medium is the Abbe number . The Sellmeier equation, on the other hand, tries to reproduce the empirically determined course of the refractive index over the wavelength . There is also a simpler description using the Cauchy equation . In addition, there are numerous other dispersion formulas, e.g. B .: ${\ displaystyle n}$ ${\ displaystyle \ lambda}$

Helmholtz-Ketteler-Drude dispersion formula,
Schott dispersion formulas,
Geffcken's dispersion formula,
Buchdahl's dispersion formula,
Kettler's dispersion formula,
Kramers-Heisenberg dispersion formula,
Breit-Wigner dispersion formula,
Hartmann's dispersion formula,
Herzberg's dispersion formula (for the visual area) or
as a polynomial formula: ${\ displaystyle n ^ {2} (\ lambda) = \ sum _ {i = 1} ^ {6} A_ {i} \ lambda ^ {4-2i}}$

Effects

The dispersion of the phase velocity determines the dispersion of the group velocity .

Phase velocity dispersion

A prism splits light into its color spectrum.
Images using lenses show undesirable color fringes , which can be corrected by combining lenses made of optical glasses with different dispersion (see achromat and apochromat ).
Magnetic lenses such as those of an electron microscope also show dispersion depending on the speed of the electrons. Countermeasures are a narrow energy distribution of the electrons, from field instead of glow emission , a high acceleration voltage and a small aperture .

Group velocity dispersion

Light pulses in optical fibers , which are for example used in optical data transmission experienced due to the group velocity dispersion a broadening during transmission. The shorter the duration of a light pulse, the broader its frequency spectrum and the more pronounced the change in the shape of the pulse, especially on long transmission paths (see dispersion in optical fibers ).
Depending on the frequency, electrical cables have different propagation speeds due to their insulating materials . B. shows in the time domain reflectometry on broadened reflected pulses. The effect leads to delay time distortions in broadband signals (for example in the form of flatter pulse edges) and can be avoided by using suitable insulating materials.
The distance-dependent change in the thunder sound from bang to rumble is due to various dispersion effects of the sound waves on the way to the observer. The reasons for this can be different refractions of temperature and pressure changes and different deflections by winds of the different frequency components of the original popping noise.

Examples

Dispersion of water waves
Dispersion relation of phonons
Polarization mode dispersion in optical fibers

Individual evidence

↑ Glassproperties.com Calculation of the Mean Dispersion of Glasses (in English).
^ Hans Bach, Norbert Neuroth: The Properties of Optical Glass . Springer, 1995, ISBN 978-3-540-58357-8 , pp. 19-27 .
↑ Rainer Dohlus: Photonics: Physical-technical basics of light sources, optics and lasers . Oldenbourg Verlag, 2010, ISBN 978-3-486-58880-4 , pp. 277 .
↑ Max Herzberger: Color Correction in Optical Systems and a New Dispersion Formula . In: Journal of Modern Optics . tape 6 , no. 3 , 1959, pp. 197-215 .

[1] Glassproperties.com Calculation of the Mean Dispersion of Glasses (in English).

[2] Hans Bach, Norbert Neuroth: The Properties of Optical Glass . Springer, 1995, ISBN 978-3-540-58357-8 , pp. 19-27 .

[3] Rainer Dohlus: Photonics: Physical-technical basics of light sources, optics and lasers . Oldenbourg Verlag, 2010, ISBN 978-3-486-58880-4 , pp. 277 .

[4] Max Herzberger: Color Correction in Optical Systems and a New Dispersion Formula . In: Journal of Modern Optics . tape 6 , no. 3 , 1959, pp. 197-215 .