Harmonic oscillator (quantum mechanics)

The harmonic oscillator in quantum mechanics describes the behavior of a particle in a potential of form , analogous to the harmonic oscillator in classical physics

${\displaystyle V(x)={\frac {1}{2}}kx^{2}={\frac {1}{2}}m\omega ^{2}x^{2}}$.

with x deflection, k reference variable , m mass, ω angular frequency

Such a square potential is also known as a harmonic potential. Classically obtained this potential for a system whose restoring force proportional to the displacement from the rest position.

Since any potential in the vicinity of a stable equilibrium position can be approximately described as a harmonic potential, this is one of the most important model systems in quantum mechanics. It is also one of the few quantum mechanical systems for which an exact analytical solution is known.

Hamilton operator and eigenstates in the one-dimensional case

The Hamilton operator or energy operator, which describes the total energy ( kinetic energy + potential energy ) in quantum mechanics , is for the harmonic oscillator

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {m\omega ^{2}{\hat {x}}^{2}}{2}}=-{\frac {\hbar ^{2}}{2m}}\Delta +{\frac {m\omega ^{2}x^{2}}{2}}.}$

Here is the particle mass and the natural angular frequency of the oscillator. In the position representation is the position operator and the momentum operator . The squared local derivative is expressed by the Laplace operator . ${\displaystyle m}$ ${\displaystyle \omega }$ ${\displaystyle {\hat {x}}=x}$ ${\displaystyle {\hat {p}}=-\mathrm {i} \hbar \nabla }$ ${\displaystyle \nabla ^{2}=\Delta }$

The stationary Schrödinger equation

${\displaystyle {\hat {H}}\psi _{n}(x)=E_{n}\psi _{n}(x)}$

is thus for the one-dimensional harmonic oscillator

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\Delta \psi _{n}(x)+{\frac {1}{2}}m\omega ^{2}x^{2}\psi _{n}(x)=E_{n}\psi _{n}(x).}$

Spatial wave functions of a particle in the harmonic potential in the states n = 0… 7

Residency probability density belonging to the location wave functions.

The eigenfunctions of the harmonic oscillator result from solving this linear differential equation . These solutions are the Hermite functions (derivation possible e.g. via the ladder operator method): ${\displaystyle \psi _{n}(x)}$

${\displaystyle \psi _{n}(x)=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}{\frac {1}{\sqrt {2^{n}n!}}}H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)e^{-{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}}$.

Here are the Hermite polynomials : ${\displaystyle H_{n}(y)}$

${\displaystyle H_{n}(y)=(-1)^{n}e^{y^{2}}{\frac {\mathrm {d} ^{n}}{\mathrm {d} y^{n}}}\left(e^{-y^{2}}\right)}$ or equivalent ${\displaystyle H_{n}(y)=e^{\frac {y^{2}}{2}}\,\left(y-{\frac {\mathrm {d} }{\mathrm {d} y}}\right)^{n}\,e^{-{\frac {y^{2}}{2}}}\,,}$

so

${\displaystyle {\begin{aligned}H_{0}(y)&=1\\H_{1}(y)&=2y\\H_{2}(y)&=(2y)^{2}-2=4y^{2}-2\\H_{3}(y)&=(2y)^{3}-6(2y)=8y^{3}-12y\\H_{4}(y)&=(2y)^{4}-12(2y)^{2}+12=16y^{4}-48y^{2}+12\\\ldots \end{aligned}}}$

The term describes the exponential drop outside the oscillator potential. When calculating by hand, the following relation is often useful: ${\displaystyle e^{-{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}}$

${\displaystyle \int _{-\infty }^{\infty }x^{2n}e^{-ax^{2}}dx=\Gamma \left({\frac {1}{2}}+n\right){\sqrt {\frac {1}{a^{2n+1}}}}={\frac {(2n-1)!!}{2^{n}}}{\sqrt {\pi }}{\sqrt {\frac {1}{a^{2n+1}}}}={\frac {1\cdot 3\cdot 5\cdot \ldots \cdot \left(2n-1\right)}{2^{n}}}{\sqrt {\frac {\pi }{a^{2n+1}}}}}$.

The basic state has the form of a Gaussian curve ${\displaystyle n=0}$

${\displaystyle \psi _{0}(x)=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}e^{-{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}}$.

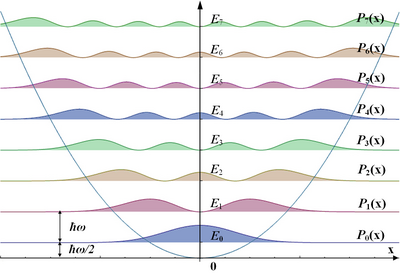
The upper graphic opposite shows the first eight solutions for the wave function , including the square of the magnitude , which indicates the probability of a particle being located. The given harmonic potential is the blue parabola. The heights of the zero lines correspond to the energy levels ${\displaystyle \psi _{n}(x)}$

${\displaystyle E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right)}$

of the solutions.

Zero point energy

Comparison between classic and quantum mechanical oscillator

→ Main article : Zero point energy

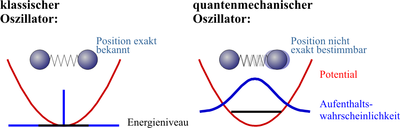
The state with the lowest energy is thus above the minimum potential. As a result, in accordance with Heisenberg's uncertainty principle , the particle is not exactly localized at, as one would expect from a classical oscillator. One speaks here of a zero point energy or zero point oscillation. In quantum field theories , this leads to vacuum fluctuations . ${\displaystyle E_{0}={\frac {1}{2}}\hbar \omega }$ ${\displaystyle x=0,p=0}$

The ladder operator method

The problem of the harmonic oscillator in quantum mechanics can be treated by means of creation and annihilation operators . The method was developed by Paul Dirac , based on the work of Niels Bohr and Otto Wiener . This approach is also called the algebraic method .

For this approach, two operators and are defined , which each add or remove an energy quantum from an oscillator . That is why they are called annihilation and creation operators. Other common names are ladder operator and step up / down operator. The notation is converted to the simpler notation (see also Bra-Ket notation ). Such a state is called the Fock state or occupation number state because it indicates the number of energy quanta in the oscillator. These operators are defined in such a way that they satisfy the following relationships: ${\displaystyle {\hat {a}}}$ ${\displaystyle {\hat {a}}^{\dagger }}$ ${\displaystyle \hbar \omega }$ ${\displaystyle \psi _{n}(x)}$ ${\displaystyle \left|n\right\rangle }$ ${\displaystyle n}$

${\displaystyle {\begin{aligned}{\hat {a}}\left|n\right\rangle &:={\sqrt {n}}\,\left|n-1\right\rangle \\{\hat {a}}^{\dagger }\left|n\right\rangle &:={\sqrt {n+1}}\,\left|n+1\right\rangle \end{aligned}}}$

The application of leads from an eigenstate to the eigenstate with a lower energy level, the application of transforms in the opposite direction. From these operators the occupation number operator can be put together, which gives the number of energy quanta in a state (i.e. the number ): ${\displaystyle {\hat {a}}}$ ${\displaystyle \left|n\right\rangle }$ ${\displaystyle \left|n-1\right\rangle }$ ${\displaystyle {\hat {a}}^{\dagger }}$ ${\displaystyle {\hat {n}}={\hat {a}}^{\dagger }{\hat {a}}}$ ${\displaystyle n}$

${\displaystyle {\hat {n}}\left|n\right\rangle =n\left|n\right\rangle }$

Now the Hamilton operator can be rewritten with these new operators as:

${\displaystyle {\hat {H}}=\hbar \omega \left({\hat {a}}^{\dagger }{\hat {a}}+{\frac {1}{2}}\right)=\hbar \omega \left({\hat {n}}+{\frac {1}{2}}\right)}$

The operators and can be represented by the canonical operators and : ${\displaystyle {\hat {a}}}$ ${\displaystyle {\hat {a}}^{\dagger }}$ ${\displaystyle {\hat {x}}}$ ${\displaystyle {\hat {p}}}$

• Annihilation operator: ${\displaystyle {\hat {a}}={\sqrt {\frac {m{\omega }}{2\hbar }}}\left({\hat {x}}+{\frac {\mathrm {i} {\hat {p}}}{m{\omega }}}\right)}$
• Creation operator: ${\displaystyle {\hat {a}}^{\dagger }={\sqrt {\frac {m{\omega }}{2\hbar }}}\left({\hat {x}}-{\frac {\mathrm {i} {\hat {p}}}{m\omega }}\right)}$

This directly follows the representation of as well as : ${\displaystyle {\hat {x}}}$ ${\displaystyle {\hat {p}}}$

${\displaystyle {\hat {x}}={\sqrt {\frac {\hbar }{2m\omega }}}\left({\hat {a}}^{\dagger }+{\hat {a}}\right)}$

${\displaystyle {\hat {p}}=\mathrm {i} {\sqrt {\frac {m\omega \hbar }{2}}}\left({\hat {a}}^{\dagger }-{\hat {a}}\right).}$

To determine the eigenfunctions, the Schrödinger equation for the lowest state can be solved explicitly (this is a simple differential equation) and thus receives its position representation. All other states are then obtained through the recursive application of the creation operator to this basic state: ${\displaystyle \left|0\right\rangle }$

${\displaystyle \left|n\right\rangle ={\frac {1}{\sqrt {n!}}}\left({\hat {a}}^{\dagger }\right)^{n}\left|0\right\rangle }$

From this expression (in the following by substitution with and use of the definition of the Hermite polynomials) the above representation of as Hermite function (in spatial space) can be derived: ${\textstyle y(x)={\sqrt {\frac {m\omega }{\hbar }}}x}$ ${\textstyle {\frac {\mathrm {d} }{\mathrm {d} x}}={\frac {\mathrm {d} y}{\mathrm {d} x}}{\frac {\mathrm {d} }{\mathrm {d} y}}={\sqrt {\frac {m\omega }{\hbar }}}{\frac {\mathrm {d} }{\mathrm {d} y}}}$ ${\textstyle \left|n\right\rangle :=\psi _{n}(x)}$

${\displaystyle {\begin{aligned}\left|n\right\rangle =\psi _{n}(x)&={\frac {1}{\sqrt {n!}}}\left({\hat {a}}^{\dagger }\right)^{n}\psi _{0}(x)\\&={\frac {1}{\sqrt {n!}}}{\frac {1}{\sqrt {2^{n}}}}\left({\sqrt {\frac {m{\omega }}{\hbar }}}\right)^{n}\left(x-{\frac {\hbar }{m\omega }}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}\psi _{0}(x)\\&={\frac {1}{\sqrt {{2^{n}}n!}}}\left({\sqrt {\frac {m{\omega }}{\hbar }}}\right)^{n}\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}\left(x-{\frac {\hbar }{m\omega }}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}e^{-{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}\\&={\frac {1}{\sqrt {{2^{n}}n!}}}\left({\sqrt {\frac {m{\omega }}{\hbar }}}\right)^{n}\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}e^{-{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}e^{{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}\left(x-{\frac {\hbar }{m\omega }}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}e^{-{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}\\&\vdots \\&={\frac {1}{\sqrt {{2^{n}}n!}}}\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}e^{-{\frac {1}{2}}{\frac {m\omega }{\hbar }}x^{2}}H_{n}\left(y(x)\right)\\&={\frac {1}{\sqrt {{2^{n}}n!}}}H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)\psi _{0}(x).\end{aligned}}}$

In the same way, quantum-mechanical particles or fields can be described. If, for example, one imagines electromagnetic radiation composed of photons , then operators can also set up creation and annihilation operators for photons. It turns out that the electromagnetic field can be described as a collection of harmonic oscillators. Each oscillator stands for a light wave of a certain frequency . It indicates the number of photons in this "mode" of the light field. Such a procedure is generally called second quantization . A detailed calculation of the eigenvalues ​​of the (one-dimensional) oscillator can be found in the article Creation and Annihilation Operator under Bosonic Climbing Operators . ${\displaystyle \omega }$ ${\displaystyle n}$

Classic borderline case

In the borderline case of large quantum numbers , the probability of stay changes over to the classic probability of stay. This classical probability density is proportional to the inverse speed . The lower the speed of the classical particle in the potential, the longer it stays in a corresponding place. The speed can be derived directly from the energy law. The following figure shows the classical and the quantum mechanical probability density. The bigger it gets, the more similar the curves become: ${\displaystyle n}$ ${\displaystyle 1/v}$ ${\displaystyle v}$ ${\displaystyle n}$

Comparison between the location-dependent probability density of a QM oscillator (blue) at n = 70 and that of a classic oscillator (purple).

Quasi-classical states

Time development of a quasi-classical state in harmonic potential

If you bring a localized wave packet into a harmonic potential (see figure on the right), it behaves like a classical particle in this potential (hence a quasi-classical state). If it hits the potential edges, it will turn around and run back. It then effectively vibrates in potential.

Mathematically, these states correspond to coherent states . They are characterized by a complex number and can be represented as a linear combination of the states : ${\displaystyle \alpha }$ ${\displaystyle \left|n\right\rangle }$

${\displaystyle \left|\alpha \right\rangle =e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over {\sqrt {n!}}}\left|n\right\rangle }$

Such states are important when describing coherent radiation, as it can be shown that the light field in quantum field theory can be traced back to harmonic oscillators (one for each mode of the field) (see also coherent radiation ). The probability distribution of the population numbers of coherent states follows (like the photon statistics of coherent light) the Poisson distribution :

${\displaystyle P(n)=\left|\left\langle n|\alpha \right\rangle \right|^{2}={\frac {|\alpha |^{2n}}{n!}}e^{-|\alpha |^{2}}}$

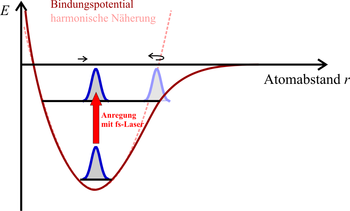
A state similar to the quasi-classical state is created when a diatomic molecule (e.g. hydrogen H ₂ ) is excited with the help of an intense femtosecond laser . It has already been explained above that the harmonic oscillator can be used as an approximation for the oscillation of diatomic molecules. The following figure shows what happens:

First, a deep, narrow wave function is raised to a higher energy state with a laser pulse. There it remains localized and begins to move as a "quasi-classical state" in potential. A second pulse is then emitted for measurement, which ionizes the molecule. The position of the wave function indicates the distance between the atoms in the molecule. From the kinetic energy of the fragments, conclusions can be drawn about this distance and the shape of the wave packet.

N-dimensional harmonic oscillator

The one-dimensional harmonic oscillator can easily be extended to the N-dimensional case. The Hamilton operator in N dimensions is

${\displaystyle {\hat {H}}=\left({{\hat {p}}^{2} \over 2m}+{1 \over 2}m\omega ^{2}{\hat {r}}^{2}\right)=\sum _{i=1}^{N}\left({{\hat {p}}_{i}^{2} \over 2m}+{1 \over 2}m\omega ^{2}{\hat {x}}_{i}^{2}\right)}$.

From this it becomes clear that the N-dimensional harmonic oscillator corresponds exactly to N independent one-dimensional harmonic oscillators with the same mass and restoring force, because a sum of N independent eigenfunctions for each coordinate according to the above one-dimensional scheme solves the Schrödinger equation. This is an advantageous property of the potential (see Pythagorean theorem ), which makes it possible to separate the potential energy into terms that only depend on one coordinate. ${\displaystyle r^{2}=x_{1}^{2}+x_{2}^{2}+\dots +x_{N}^{2}}$

The possible energy levels result accordingly

${\displaystyle E_{n}=\hbar \omega \left[(n_{1}+\cdots +n_{N})+{N \over 2}\right]=\hbar \omega \left[n+{N \over 2}\right]}$.

However, it should be noted that the energy levels of the N-dimensional oscillator are -fold degenerate according to the combinatorial possibilities for realizing the levels as follows: ${\displaystyle E_{n}}$ ${\displaystyle g_{n}}$

${\displaystyle g_{n}={\binom {N+n-1}{n}}}$

Coupled harmonic oscillators

If one considers in the simplest case a system of two one-dimensional particles, which are only coupled to one another by a harmonic force , the Hamilton operator results for this ${\displaystyle F=-k(x_{2}-x_{1})}$

${\displaystyle H={\frac {p_{1}^{2}+p_{2}^{2}}{2m}}+{\frac {1}{2}}\,k(x_{2}-x_{1})^{2}.}$

Since a simple separation of the Schrödinger equation initially prevents, a transformation in centroid coordinates is recommended: ${\displaystyle (x_{2}-x_{1})^{2}=x_{1}^{2}+x_{2}^{2}-2x_{1}x_{2}}$ ${\displaystyle x_{1}',x_{2}'}$

${\displaystyle {\begin{aligned}x_{1}':=&x_{1}+x_{2}&\qquad x_{2}':=&x_{2}-x_{1}\\x_{1}=&{\frac {x_{1}'-x_{2}'}{2}}&\qquad x_{2}=&{\frac {x_{1}'+x_{2}'}{2}}\end{aligned}}}$

The impulses can be expressed by the impulses of the centroid coordinates as

${\displaystyle p_{1}^{2}+p_{2}^{2}={\frac {p_{1}'^{2}+p_{2}'^{2}}{2}}}$.

Thus the separation of the Hamilton operator succeeds

${\displaystyle H={\frac {p_{1}'^{2}+p_{2}'^{2}}{4m}}+{\frac {1}{2}}kx_{2}'^{2}.}$

This corresponds to a single harmonic oscillator with regard to the differential oscillation of the 2 particles (with twice the reduced mass), whereby the system as a whole also moves like a free particle . The solution of the Schrödinger equation leads accordingly to the harmonic energy levels ${\displaystyle x_{2}',p_{2}'}$ ${\displaystyle (x_{1}',p_{1}')}$

${\displaystyle E_{n}=\hbar \omega _{2m}\left(n+{\frac {1}{2}}\right)+E_{\text{translation}}}$.

In a chain of N particles that are coupled in pairs in harmony with one another (one-dimensional lattice), one finds a coordinate transformation in such a way that collective harmonic oscillations (plus a communal center of gravity movement) that are independent of one another result. ${\displaystyle {\vec {x}}'=M{\vec {x}}}$ ${\displaystyle N-1}$

In the case of three-dimensional crystal lattices in solid state physics , this consideration then leads to the phonons .

Applications

The harmonic oscillator is an important model system in quantum physics, as it is one of the few closed (i.e. without approximations and numerical methods ) solvable systems of quantum mechanics. With it, a number of physical facts can be approximately described:

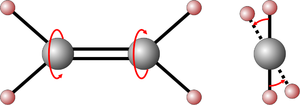
• In molecular physics it allows an approximation of the bonding relationships between atoms and thus enables e.g. B. a prediction of vibration spectra . This can be illustrated by showing a bond through two mass points (the atoms) that are connected to one another by a spring (harmonic potential) and oscillate against each other:

The linear restoring force of such a spring leads to a harmonic potential (proportional ) and thus to the harmonic oscillator. In real molecules the potential looks a little different (compare Morse potential ), but the harmonic oscillator is a good approximation, at least for low vibrational energies. ${\displaystyle F(x)}$ ${\displaystyle V(x)}$ ${\displaystyle x^{2}}$

• Another example is the torsional vibration of the ethene molecule , which is shown in the following drawing:

In doing so, the double bond is twisted, so to speak, and two hydrogen atoms swing against each other while rotating.

• In modern atomic physics , atoms and ions to be examined are caught and cooled in optical traps or ion traps in order to e.g. B. to get a higher resolution for measurements. In addition, new states of matter can be examined in such cases (e.g. Bose-Einstein condensates , Fermi condensates ). Such traps have, as a first approximation, a parabolic potential. Thus, particles in these cases can also be described with the model of the quantum mechanical harmonic oscillator.
• In solid-state physics , the Einstein model (according to Albert Einstein ) describes a method to calculate the contribution of the lattice vibrations ( phonons ) to the heat capacity of a crystalline solid. The basis is the description of the solid as consisting of N quantum harmonic oscillators, each of which can oscillate independently in three directions. In addition, phonons can also be described by a collection of coupled harmonic oscillators. Each atom in the crystal lattice is an oscillator that is coupled to its neighboring atoms.

swell

• Claude Cohen-Tannoudji , Bernard Diu, Franck Laloë, Franck: Quantum Mechanics 1/2. , 2nd edition, Walter de Gruyter, Berlin - New York 1999
• Jun John Sakurai : Modern Quantum Mechanics . Addison-Wesley

Web links

• Complete solution of the harmonic oscillator using the algebraic method (from page 63; PDF file; 4.26 MB)
• Representation of the direct solution of the harmonic oscillator in the position representation

Individual evidence

1. ↑ Th. Ergler, A. Rudenko, B. Feuerstein, et.al .: Time-Resolved Imaging and Manipulation of H ₂ Fragmentation Intense Laser Fields In: Phys. Rev. Lett. 95, 093001, 2005
2. ^ Armstrong, Zinner, Fedorov, Jensen: Analytic Harmonic Approach to the N-body problem . In: Journal of Physics B: Atomic, Molecular and Optical Physics . 44, No. 5, 2011, p. 055303. arxiv : 1011.2453v2 . bibcode : 2011JPhB ... 44e5303A . doi : 10.1088 / 0953-4075 / 44/5/055303 .