Quantum mechanics

The quantum mechanics is a physical theory , with the features and principles of states and operations of the matter will be described. In contrast to the theories of classical physics , it allows the correct calculation of physical properties of matter in the size range of atoms and below. Quantum mechanics is one of the main pillars of modern physics . It forms the basis for the description of the phenomena of atomic physics , solid state physics and nuclear and elementary particle physics , but also related sciences such as quantum chemistry .
Basics
The basics of quantum mechanics were developed between 1925 and 1932 by Werner Heisenberg , Erwin Schrödinger , Max Born , Pascual Jordan , Wolfgang Pauli , Paul Dirac , John von Neumann and other physicists, after first classical physics and then the older quantum theories in the systematic description the processes in the atoms had failed. Quantum mechanics got its name based on and differentiated from classical mechanics . Like these, quantum mechanics remains on the one hand limited to the movement of particles with mass under the action of forces and deals with e.g. B. no formation and destruction processes yet. On the other hand, some central terms of classical mechanics, including “location” and “orbit” of a particle, are being replaced by fundamentally different concepts that are better adapted to quantum physics.
Quantum mechanics refers to material objects and models them as individual particles or as systems that consist of a certain number of individual particles. With these models, elementary particles , atoms , molecules or macroscopic matter can be described in detail. A mathematical formalism specific to quantum mechanics is used to calculate their possible states with their respective physical properties and modes of reaction .
Quantum mechanics differs fundamentally from classical physics not only in its mathematical structure. It uses terms and concepts that elude clarity and also contradict some principles that are considered fundamental and self-evident in classical physics. By applying correspondence rules and concepts of decoherence theory , many laws of classical physics, in particular all of classical mechanics, can be described as borderline cases of quantum mechanics. However, there are also numerous quantum effects without a classic borderline case. To interpret the theory, a number of different interpretations of quantum mechanics have been developed, which differ in particular in their conception of the measurement process and in their metaphysical premises.
The advanced quantum field theories are based on quantum mechanics and their terms , starting with quantum electrodynamics from around 1930, which can also be used to analyze the processes of creating and annihilating particles.
More detailed information on the mathematical formalism can be found in the article Mathematical structure of quantum mechanics .
history

At the beginning of the 20th century, the development of quantum physics began with the so-called old quantum theories . In 1900, Max Planck hypothesized to derive the radiation law named after him that an oscillator can only absorb or release energy in whole-number multiples of the energy quantum (h is Planck's quantum of action , is the frequency of the oscillator). In 1905 Albert Einstein explained the photoelectric effect using the light quantum hypothesis . Accordingly, light consists of discrete particles of the same energy , which with the frequency also have a wave property.
In the period from 1913 onwards, Niels Bohr developed the atomic model named after him . This is based on the assumption that electrons in the atom can only assume states of very specific energies and that the electrons “jump” from one energy level to another when they emit or absorb light (see electronic transition ). When formulating his theory, Bohr used the correspondence principle , according to which the quantum-theoretically calculated optical spectrum of atoms must approach the classically calculated spectrum in the limiting case of large quantum numbers. With the Bohr atomic model and its extensions, the shell model and the Bohr-Sommerfeld model , some successes were achieved, including the explanation of the hydrogen spectrum, the X-ray lines and the Stark effect as well as the explanation of the structure of the periodic table of the elements .
However, these early atomic models quickly proved to be inadequate. So they failed already in the application to the excitation spectrum of helium, in the value of the orbital angular momentum of the electronic ground state of hydrogen and in the description of various spectroscopic observations, such as B. the anomalous Zeeman effect or the fine structure .
In 1924 Louis de Broglie published his theory of matter waves , according to which any matter can have a wave character and, conversely, waves can also have a particle character. This work traced the quantum phenomena back to a common explanation, which, however, was again of a heuristic nature and also did not allow the calculation of the spectra of atoms. Therefore it is the last to be assigned to the old quantum theories, but it was trend-setting for the development of quantum mechanics.
Modern quantum mechanics began in 1925 with the formulation of matrix mechanics by Werner Heisenberg , Max Born and Pascual Jordan . While Heisenberg had spoken of “quantum theoretical mechanics” in the first of these articles, the term “quantum mechanics” , which is still used today, was coined in the two later articles . A few months later, Erwin Schrödinger presented a completely different approach - based on De Broglie's theory of matter waves - wave mechanics or the Schrödinger equation . Shortly afterwards, Schrödinger was able to prove that wave mechanics is mathematically equivalent to matrix mechanics. As early as 1926, JH Van Vleck published the first textbook on new quantum mechanics in the USA under the title Quantum Principles and Line Spectra . The first German-language textbook, Group Theory and Quantum Mechanics by the mathematician Hermann Weyl , followed in 1928.
Heisenberg discovered the uncertainty relation named after him in 1927; In the same year, the Copenhagen interpretation of quantum mechanics , which still prevails today, was formulated. In the years from around 1927 onwards, Paul Dirac combined quantum mechanics with the special theory of relativity . He also first introduced the use of operator theory, including the Bra-Ket notation, and described this mathematical calculus in his 1930 book Principles of Quantum Mechanics . At the same time, John von Neumann formulated a strict mathematical basis for quantum mechanics within the framework of the theory of linear operators on Hilbert spaces , which he described in 1932 in his book Mathematical Fundamentals of Quantum Mechanics . The results formulated in this development phase are still valid today and are generally used to describe quantum mechanical tasks.
Basic properties
This representation is based on the Copenhagen interpretation of quantum mechanics, which was developed from 1927 mainly by Niels Bohr and Werner Heisenberg. Despite its conceptual and logical difficulties, it still has a predominant position over other interpretations . In the following, formulas are largely dispensed with; for more details, see Mathematical Structure of Quantum Mechanics .
Observables and states
In the context of classical mechanics, the trajectory of a (punctiform) particle can be fully calculated in advance from the location and speed of a (point-shaped) particle, provided the forces involved are known . The state of the particle can therefore be clearly described by two quantities, which (always in ideal measurements) can be measured with unambiguous results. A separate treatment of the state and the measured variables (or " observables ") is therefore not necessary in classical mechanics, because the state determines the measured values and vice versa.
However, nature shows quantum phenomena that cannot be described with these terms. In general, it is no longer possible to predict where and with what speed a particle will be detected. If, for example, a scattering experiment is repeated with a particle under exactly the same starting conditions, one must always assume the same state for the particle after the scattering process (see Deterministic time evolution ), but it can strike at different locations on the screen. The state of the particle after the scattering process does not determine its flight direction. In general, the following applies: In quantum mechanics there are states that do not allow the prediction of an individual measurement result even if the state is exactly known. Only one probability can then be assigned to each of the possible measured values . Therefore, in quantum mechanics, measured quantities and states are treated separately and different concepts are used for these quantities than in classical mechanics.
In quantum mechanics, mathematical objects, the so-called observables, are assigned to all measurable properties of a physical system. Examples are the location of a particle, its momentum , its angular momentum or its energy . For every observable there is a set of special states in which the result of a measurement cannot scatter, but is clearly fixed. Such a state is called the “ eigenstate ” of the observable in question, and the associated measurement result is one of the “ eigenvalues ” of the observables. In all other states that are not an eigenstate of this observable, different measurement results are possible. What is certain, however, is that one of the eigenvalues is determined during this measurement and that the system is then in the corresponding eigenstate of these observables. Regarding the question of which of the eigenvalues is to be expected for the second observable or - equivalent - in which state the system will be after this measurement, only one probability distribution can be given, which can be determined from the initial state.
Different observables generally have different eigenstates. Then for a system that is the initial state in the eigenstate of an observable, the measurement result of a second observable is indefinite. The initial state itself is interpreted as a superposition ( superposition ) of all possible eigenstates of the second observable. The proportion of a certain eigenstate is called its probability amplitude . The square of the magnitude of a probability amplitude indicates the probability of receiving the corresponding eigenvalue of the second observable when measuring the initial state (Born's rule or Born's probability interpretation ). In general, any quantum mechanical state can be represented as a superposition of different eigenstates of an observable. Different states only differ in which of these eigenstates contribute to the superposition and with what proportion.
For some observables, for example angular momentum, only discrete eigenvalues are allowed. In the case of the particle location, however, the eigenvalues form a continuum . The probability amplitude for finding the particle at a certain location is therefore given in the form of a location-dependent function, the so-called wave function . The square of the magnitude of the wave function at a certain location indicates the spatial density of the probability of finding the particle there.
Not all quantum mechanical observables have a classical counterpart. One example is spin , which cannot be traced back to properties known from classical physics such as charge, mass, position or momentum.
Mathematical formulation
For the mathematical treatment of physical processes, the state of the system under consideration at the time under consideration should contain all information that - given known external forces - are required to calculate its future behavior. Therefore, the state of a mass point at a certain point in time t in classical physics is already given by specifying the position and momentum, i.e. together by a point in a 6-dimensional space called the state space or phase space . It is precisely in this definition that the quantum phenomena cannot find an explanation in classical physics. This is shown, for example, in the Heisenberg uncertainty principle described below, according to which the position and momentum of a quantum object cannot in principle be uniquely determined at the same time.
In quantum mechanics, the state is represented by a vector in Hilbert space , the usual notation is simplified and is often only written. It must be taken into account that two different vectors designate the same physical state if they only differ by a constant number factor. One of many ways to represent is the wave function (the whole function, not just its value in one place ), often also simply written as. If you look at the development of the state over time, you respectively write two wave functions that differ only by a constant factor, reflect the same state.
An observable is generally represented by a linear operator that acts mathematically on a state vector and generates a new vector of the state space as a result: If this observable is an eigenstate, the eigenvalue equation applies where the factor is the eigenvalue, i.e. the one that is clearly defined for this state Measured value of the observable The state vector is then usually identified by a lower index, e.g. B. or where the eigenvalue itself is or n (the "quantum number") is its serial number in the list of all eigenvalues (if such a list exists, i.e. not for continuous eigenvalues).
Deterministic time development
The description of the temporal development of an isolated system is carried out in quantum mechanics analogous to classical mechanics by an equation of motion, the Schrödinger equation. By solving this differential equation one can calculate how the wave function of the system develops:
with the Hamilton operator , which describes the total energy of the quantum mechanical system. The Hamilton operator is composed of a term for the kinetic energy of the particles in the system and a second term, which describes the interactions between them in the case of several particles and the potential energy in the case of external fields , whereby the external fields can also be time-dependent . In contrast to Newtonian mechanics , interactions between different particles are not described as forces , but rather, similar to the methodology of classical Hamiltonian mechanics, as energy terms. In the typical applications on atoms, molecules, solids, the electromagnetic interaction is particularly relevant.
The Schrödinger equation is a partial differential equation of the first order in the time coordinate, so the time evolution of the quantum mechanical state of a closed system is completely deterministic .
Stationary conditions
If the Hamilton operator of a system does not itself depend on time, there are stationary states for this system, i.e. those that do not change over time. They are the eigen-states of the Hamilton operator . Only in them does the system have a well-defined energy , precisely the respective eigenvalue:
In this case, the Schrödinger equation is reduced to
and has the solution
The development over time is only expressed in an additional exponential factor , a phase factor . This means that the state described by is the same as - a stationary state. Only the quantum mechanical phase changes, with the angular frequency . Even for observables other than energy, the probability of measuring a certain value in stationary states is independent of time.
interference
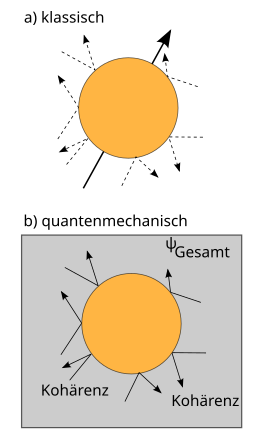
Another essential property of the quantum mechanical state is the possibility of interference. If z. B. and are solutions of the same Schrödinger equation, it is also their sum . This property expresses the principle of superposition, which applies to waves of all kinds . Mathematically, it results here from the linearity of the Schrödinger equation. The corresponding spatial probability distribution for a particle in the state is given (except for a constant normalization factor) by the square of the absolute value. In the state the probability of stay is therefore not the sum of the two individual probabilities of stay and , as one would expect for classical particles. Rather, it is zero at every location where applies (destructive interference), while at locations it is twice as large as the sum of the two individual probabilities of being located (constructive interference). This property is also exhibited by light which, for example, creates an interference pattern behind a double slit . Quantum mechanics predicts similar interference phenomena for particles as for light.
The double slit experiment shows both the statistical nature of quantum mechanics and the interference effect and is thus a good example of wave-particle dualism . Microscopic "particles", for example electrons, are sent in a wide beam onto an obstacle with two closely spaced slits and collected further back on a fluorescent screen. In the distribution of electrons on the screen, assuming the classical particle model, one would expect two clusters that can be clearly distinguished from one another. You can think of it as letting small balls fall through two slits from above; these will form a pile under each slot. The measurement results actually observed with electrons are different (see figure on the right). They only agree with the classical idea of particles in so far as each individual electron causes exactly one luminous point on the screen. When carrying out the experiment with many electrons (regardless of whether they are sent to the column at the same time or one after the other), the probability distribution of the measured position values becomes visible, which does not correspond to the two classically expected accumulations. Instead, as with light, it has pronounced interference fringes in which the destructive and constructive interference alternate.
Measurement process
A measurement on a physical object determines the instantaneous value of a physical quantity. In the formalism of quantum mechanics, the measured quantity is described by an operator, and the measured value is an eigenvalue of this operator. In general, the states of the system are superimpositions of eigenstates to different eigenvalues, but a single measurement does not result in a blurred picture of several values, but always a unique value. The measurement also establishes that the object at this point in time assumes an eigenstate of the operator belonging to this eigenvalue. If it is a measurement that leaves the object intact, an immediate repetition of the measurement must certainly deliver the same result, because every change in the state according to the Schrödinger equation would take a certain amount of time.
The quantum mechanical measurement problem arises from the fact that the transition from the state before the measurement to the state determined by the measurement cannot be understood as a development over time according to the Schrödinger equation. This transition is known as the collapse of the wave function or state reduction. Of the components that the wave function has before the measurement, all those that belong to eigenvalues other than the determined measured value disappear in the collapse. In the corresponding formulations of quantum mechanics, this collapse occurs during the measurement process . But this is only an imprecise and unsatisfactory description in everyday language. The processes in the measuring apparatus are without exception physical processes. But if quantum mechanics is the correct fundamental theory of all physical processes, it should be able to describe all physical systems - including the measuring device itself - and their mutual effects on one another. According to quantum mechanics, the measuring process transfers the system under investigation and the measuring device to a state in which they are entangled with one another. When the measurement result is then determined - at the latest by reading it on the measuring device - the problem of condition reduction arises again. Apparently there is a lack of a definition in physical terms what exactly makes the difference between a “measurement” and all other physical processes, so that it can cause the collapse of the wave function. In particular, it remains open where the boundary between the quantum system to be described and the classic "measuring apparatus" should be determined. This is known as the demarcation problem. For the concrete prediction of the probability distribution of the measurement results on the system under investigation, however, it is irrelevant where this limit is drawn, i.e. which parts of the measurement apparatus are included in the quantum mechanical analysis. The only thing that is certain is that the condition must be reduced between the start of the measurement and the registration of the individual, unambiguous results.
The Copenhagen interpretation does not explain the collapse and the questions about demarcation any further: A measurement is simply described as the interaction of a quantum system with a measuring device , which is itself understood as a classical physical system. The description of observables and states given above is based on this interpretation. The interpretation according to the many worlds theory is very different from this . It does not regard the components that have disappeared in the collapse as having disappeared, but assumes that in the measurement for each individual component a new universe is created in which it is the only one to continue to exist. For these and other perspectives see Interpretations of Quantum Mechanics .
Another important difference between the quantum mechanical and the classical measurement becomes evident in successive measurements of two different quantities. Since the (ideal) classical measurement does not change the measured system at all, the sequence of the two measurements has no effect on the results. According to quantum mechanics, however, the initial state is generally changed by a measurement, unless it is already an eigenstate of the observable in question. In the case of two successive measurements, the sequence is therefore only irrelevant if the system is in a common eigenstate of both observables. Otherwise a state reduction occurs in at least one of the measurements and the relevant measurement result can only be predicted with probability. This is always the case for certain pairs of observables, because they have no common eigen-state at all. Such observables are called complementary observables . An example of a pair of complementary observables are position and momentum. Has z. For example, if a particle has a certain momentum, a measurement of the momentum will give exactly this value. A subsequent location measurement then gives a value from an infinitely broad probability distribution, because with a fixed impulse the location is completely indefinite. However, if the sequence is reversed, i.e. the location measurement is carried out first, the impulse is then indefinite, and thus also the result of the subsequent impulse measurement.
Heisenberg's uncertainty principle
The uncertainty principle of quantum mechanics, known in the form of Heisenberg's uncertainty principle, relates the smallest possible theoretically achievable uncertainty ranges of two measured quantities. It applies to every pair of complementary observables , in particular to pairs of observables that describe physical measured quantities such as position and momentum or angle of rotation and angular momentum , which in classical mechanics are called canonically conjugated and can assume continuous values.
If one of these variables has an exactly determined value for the system under consideration (uncertainty range zero), then the value of the other is completely indeterminate (uncertainty range infinite). This extreme case is only of theoretical interest because no real measurement can be completely exact. In fact, the final state of the measurement of the observables is therefore not a pure eigenstate of the observables , but rather a superposition of several of these states to form a certain range of eigenvalues . If one denotes with the uncertainty range of , mathematically defined by the so-called standard deviation , then the inequality applies to the uncertainty range of the canonically conjugated observables, which is also defined
- .
Therein is the Planck's constant and .
Even if both measuring devices can measure as precisely as required, the sharpness of the measurement of is limited by that of the measurement of . There is no state in which the measured values of two canonically conjugate observables scatter with less uncertainty. For the example of position and momentum, this means that in quantum mechanics the description of the movement of a particle through a trajectory curve is only meaningful with limited accuracy and, in particular, is impossible in the interior of an atom.
A similar uncertainty relation applies between energy and time. However, this takes on a special role here, since in quantum mechanics no observable is assigned to time for formal reasons.
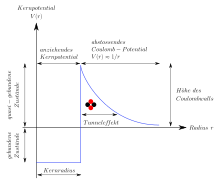
Tunnel effect
The tunnel effect is one of the more well-known quantum effects that stand in contrast to classical physics and everyday experience. It describes the behavior of a particle at a potential barrier . In the context of classical mechanics, a particle can only overcome such a barrier if its energy is higher than the highest point of the barrier, otherwise it will bounce off. According to quantum mechanics, on the other hand, the particle can with a certain probability overcome the barrier even in the classically forbidden case. On the other hand, there is a certain probability that the particle will also be reflected at the barrier if its energy is higher than the barrier. The probabilities for tunneling or for reflection can be calculated precisely if the form of the potential barrier is known.
The tunnel effect is of great importance in various areas of physics, for example in the description of alpha decay , nuclear fusion , the functioning of field emission and scanning tunneling microscopy or in explaining the formation of chemical bonds .
Entanglement, EPR experiment
When two quantum systems interact with each other, they have to be viewed as a total system. Even if the quantum mechanical state of this overall system is simply composed of the two well-defined initial states of the two subsystems before the interaction, it develops through the interaction into a superposition of states, which are each formed from such pairs of states of the subsystems. Different pairings are possible with different degrees of probability (e.g. elastic or inelastic collision, or deflection at different angles, etc.). In each of these pairs, the final states of the subsystems are coordinated in such a way that the conservation laws (energy, momentum, angular momentum, charge etc.) are fulfilled. The state of the overall system is clearly established and is a superposition of all possible pairings. Unlike the initial state before the interaction, it cannot simply be formed from a specific state of both subsystems. Then, with a measurement that is only carried out on one subsystem and finds this in a certain of its possible end states, it is also clearly established that the other subsystem is in the corresponding end state. There is now a correlation between the physical properties of the subsystems. This is why the state of the overall system is called entangled . The entanglement is retained even if the point in time of the interaction is far in the past and the two subsystems have meanwhile moved far apart. For example, it is possible to prepare a pair of electrons in such a way that they are spatially distant and the direction of the spin cannot be predicted for any of the electrons individually, while it is certain that one electron has the spin “down” when the other Electron with the spin "up" was observed, and vice versa. These correlations can also be observed if it is only decided after the interaction which direction in space is defined as the up or down axis.
The result of the interlocking is that the execution of a measurement at one location influences the measurement results at another location (in principle at any distance) and without any time delay, i.e. at faster than light speed . This phenomenon was one of the reasons why Albert Einstein rejected quantum mechanics. He considered the separability or “locality” of physical systems (i.e. the existence of well-defined local physical properties) as a fundamental principle of physics and tried to prove that quantum mechanics is incomplete. To this end, in 1935, together with Boris Podolsky and Nathan Rosen, he developed a thought experiment that became known as the Einstein-Podolsky-Rosen Paradox (EPR Paradox). They showed that the principle of locality results in the existence of additional properties of the systems that are not described by quantum mechanics (so-called hidden variables ); thus the theory is incomplete. However, it remained unclear whether the locality principle known from classical physics actually also applies to quantum mechanics. It was not until 1964 that John Stewart Bell succeeded in expanding the EPR thought experiment to include the experimentally verifiable Bell inequality and thus to put the locality assumption to the test. All experiments carried out since then have shown the violation of Bell's inequality predicted by quantum mechanics and thus refuted Einstein's assumption of locality.
Furthermore, the exact theoretical analysis of the EPR effect shows that it does not contradict the special theory of relativity , since no information can be transferred in this way: The individual measurement - regardless of whether the other particle has already been measured - always results in an am Place and time of measurement unpredictable result. Only when the result of the other measurement is known - at the earliest through communication at the speed of light - can the correlation be established or exploited.
Identical particles, Pauli principle
Due to the fundamental impossibility of determining the state of a quantum physical system "completely" according to classical standards, a distinction between several particles with completely identical intrinsic properties (such as mass or charge , but not state-dependent quantities such as energy or momentum) in quantum mechanics is lost Sense. According to the ideas of classical mechanics, any precise position and momentum measurements can be carried out simultaneously on several particles - whether identical or not - from which (at least in principle) the future path of each particle can be precisely predicted. If you later find a particle at a certain place, you can clearly assign its starting point to it and say with certainty that both places were the same particle. A quantum mechanical consideration does not allow such “consecutive numbering” of identical particles. This is important because z. B. all electrons in this sense are identical particles. It is therefore impossible to answer the question, for example, whether "the same" or a "different" electron was observed in two successive measurements on individual electrons. Here the words “the same” and “different” are placed in quotation marks because they may seem clear in everyday language, but do not make any sense for identical particles. It is not only impossible to answer the question posed, it certainly cannot be asked in a physically meaningful way.
Since exchanging two identical particles does not change any of the physical properties of the state of a many-particle system , the state vector must remain the same or at most it can change its sign. Identical particles are called bosons if the state vector remains the same when they are swapped, and fermions if it changes sign. The spin statistics theorem states that all particles with an integer spin are bosons (e.g. photons) and all particles with half- integer spin are fermions. This cannot be derived in the context of quantum mechanics, but only from quantum field theory .
An important consequence is the rule known as the " Pauli Principle " that two identical fermions cannot assume the same single-particle states. In the case of atoms, it excludes multiple occupations of electronic states and forces them to be “filled” up to the Fermi energy . This is of great practical importance because it enables atoms to enter into many different chemical compounds . The spin statistics theorem also causes considerable differences in the thermodynamic behavior between systems with many identical particles. Bosons obey the Bose-Einstein statistics . B. describes the thermal radiation, fermions of the Fermi-Dirac statistics , which z. B. explains the electronic properties of conductors and semiconductors.
Further aspects
Decoherence
The decoherence is a modern concept of quantum mechanics, the extremely efficient suppression of the effects of macroscopic systems in coherence describes. In the context of quantum mechanics it can thus be explained that macroscopic systems do not show any superposition effects, that is to say (apart from a few exceptions) behave “classically”. Decoherence is therefore an important part of the correspondence principle of quantum mechanics today .
To illustrate this effect, consider the example of a macroscopic object that is exposed to the influence of isotropic light radiation - also referred to below as the environment . In the context of classical physics, the influence of incident light on the movement of the object is negligible, as the momentum transfer associated with the collision of a photon is very low and the collisions from different directions compensate each other on average. From a quantum mechanical point of view, the object is entangled with a photon with every collision (see above ), so that the object and the photon now have to be viewed as an extended overall system. The fixed phase relationships of the quantum mechanical state, which are decisive for interference effects, now extend over two subsystems, the object and the photon; one also speaks of a delocalization of coherence.
If the (partial) state of the object is considered in isolation, each collision manifests itself in a shift in its quantum mechanical phase relationships and thus in a reduction in its ability to interfere. This is a pure quantum effect that is independent of any momentum or energy transfer associated with the impact. The practically unavoidable, numerous interactions between macroscopic objects and their environment thus lead to an effective averaging of all quantum mechanical interference effects. The time scale that is characteristic of the decoherence, the decoherence time τ d , is generally extremely short under normal conditions (e.g. about 10 −26 s); the decoherence is therefore the most efficient known physical effect. In macroscopic (“classical”) objects, only those states are found that have already completed the process of decoherence and are no longer subject to it. The remaining incoherent superposition of quantum mechanical states corresponds exactly to the states of macroscopic or classical physics. The decoherence provides a quantum mechanical explanation for the classical behavior of macroscopic systems.
Relativistic quantum mechanics

Quantum mechanics was first developed without considering the special theory of relativity . The Schrödinger equation is a differential equation of the first order in time, but of the second order in the spatial coordinate, so it is not relativistically covariant . In relativistic quantum mechanics it has to be replaced by a covariant equation. After the Klein-Gordon equation , which is a partial differential equation of the second order in space and time, the Dirac equation prevailed, which can be understood as a counterpart in the first order in space and time.
With the Dirac equation, important physical phenomena observed in electrons could be explained or even predicted for the first time. While half-integer spin in non-relativistic quantum mechanics has to be introduced ad hoc as an additional construct and contrary to the rules of angular momentum quantization, its existence arises freely from the mathematical structure of the Dirac equation. It also follows correctly from the Dirac equation that the magnetic moment of the electron in relation to the spin, the gyromagnetic factor , is almost exactly twice as large as that for a rotating charge. The fine structure of the hydrogen spectrum also turns out to be a relativistic effect that can be calculated using the Dirac equation. Another successful application of the Dirac equation is the description of the angular distribution in the scattering of photons on electrons, i.e. the Compton effect , using the Klein-Nishina formula . Another correct consequence of the Dirac equation was the monstrous prediction of the existence of an antiparticle to the electron, the positron, in its day .
Despite these successes, these theories are incomplete in that they cannot describe the creation and annihilation of particles, an effect ubiquitous in highly relativistic energies. The development of quantum field theory proved to be very fruitful here . In this theory, both material objects and their interactions are described by fields that are determined according to certain quantization rules, such as e.g. B. the second quantization , are quantized. The quantum field theory not only describes the formation and annihilation of elementary particles ( pair creation , annihilation ), but also provides a deeper explanation for their indistinguishability , for the connection between spin and statistics of quantum objects and for the existence of antiparticles .
interpretation
The classical physical theories, for example classical mechanics or electrodynamics , have a clear interpretation, that is, the symbols of the theory (place, speed, force or tensions and fields) is an intuitive, clear equivalent in experiments (i.e. a measurable quantity ) assigned. Since quantum mechanics in its mathematical formulation is based on very abstract objects such as wave functions, an interpretation is no longer possible intuitively. Therefore, a number of different interpretations have been proposed since the theory was first created. They differ in their statements about the existence of quantum objects and their properties.
The viewpoints of most interpretations of quantum mechanics can be roughly divided into two groups, the instrumentalist position and the realistic position. According to the instrumentalist position, quantum mechanics, or a model developed on its basis, does not represent a representation of “reality”. Rather, this theory is merely a useful mathematical formalism that has proven itself as a tool for calculating measurement results. This pragmatic view, originally espoused by Bohr in the context of the Copenhagen Interpretation , dominated the discussion about the interpretation of quantum mechanics until the 1960s and has shaped many common textbook representations to this day.
In addition to this pragmatic variant of the Copenhagen interpretation, there are now a number of alternative interpretations which, with a few exceptions, pursue the goal of a realistic interpretation of quantum mechanics. In the philosophy of science, an interpretation is described as scientifically realistic if it assumes that the objects and structures of the theory represent true images of reality and that both its statements about observable phenomena and its statements about unobservable entities are (approximately) true can be accepted.
In many works on quantum physics, realism is equated with the principle of value definition. This principle is based on the assumption that physical properties can be assigned to a physical object which it clearly either has or does not have with a certain value . For example, one speaks of a pendulum that the pendulum (at any given time and within a given accuracy) a deflection in the description of the oscillation has .
In the Copenhagen interpretation the assumption of value definition is abandoned. A quantum object therefore generally has no such properties, rather properties only arise at the moment and in the special context of performing a measurement. The conclusion that the definition of values has to be given up is, however, imperative neither from a logical nor from an empirical point of view. For example, the De Broglie-Bohm theory ( which cannot be distinguished from the Copenhagen interpretation in the experiment) assumes that quantum objects are particles that move along well-defined trajectories, but these trajectories themselves are beyond observation.
Relationship with other physical theories
Classic borderline case
In 1923, Niels Bohr formulated the so-called correspondence principle , according to which the properties of quantum systems in the limit of large quantum numbers correspond to the laws of classical physics with high accuracy. This limit value in large systems is known as the “classic limit case” or “correspondence limit”. The background to this principle is that classical theories such as classical mechanics or classical electrodynamics were developed on macroscopic systems (springs, capacitors, etc.) and can therefore describe them very precisely. This results in the expectation that quantum mechanics in the case of “large” systems reproduces these classical properties or does not contradict them.
An important example for this connection between classical mechanics and quantum mechanics is Ehrenfest's theorem . It says that the mean values of the quantum mechanical position and momentum observables of a particle follow the classical equation of motion to a good approximation, provided that the forces acting on the particle do not vary too much with the position.
The correspondence principle is therefore an important aid in the construction and verification of quantum mechanical model systems: On the one hand, “classical” models of microscopic systems provide valuable heuristic points of reference for the quantum mechanical description of the system. On the other hand, the calculation of the classic borderline case can be used to check the plausibility of the quantum mechanical model calculations. If physically nonsensical results are obtained in the classic limit case, the corresponding model can be discarded.
Conversely, this correspondence also means that the correct quantum mechanical description of a system, including some non-classical effects such as the tunnel effect , is often possible approximately using classical terms; such approximations often allow a deeper understanding of quantum mechanical systems. One speaks here of semiclassical physics . Examples of semiclassical descriptions are the WKB approximation and the Gutzwiller trace formula .
However, the correspondence rules described above do not have universal validity, since they only apply under certain restrictive conditions and do not take decoherence (see above ) into account. Furthermore, not all quantum effects approach a classic borderline case when applying the correspondence rules. As the Schrödinger's cat thought experiment already illustrates, “small” quantum effects such as B. the decay of a radioactive atom can in principle be enlarged arbitrarily by amplifiers. Although decoherence effects in macroscopic systems usually result in a very efficient averaging of interference effects, the state of macroscopic systems still shows quantum mechanical correlations, B. can be described in the form of the so-called Leggett- Garg inequalities in an experimentally verifiable form. Another example of quantum effects for which no correspondence rule applies are the consequences of the indistinguishability of the same particles, e.g. doubling the probability of a deflection by 90 ° in the event of a collision (along with other interference phenomena in the angular distribution), regardless of how low the energy of the particles is and how far apart they remain if there are only two identical bosons (e.g. α-particles).
Relation to the general theory of relativity
Since the gravitational force is very weak compared to the other basic forces in physics , general relativistic effects mainly occur with massive objects, such as B. stars or black holes , while quantum effects are predominantly observed in microscopic systems. Therefore, there is little empirical data on quantum effects caused by gravity. The few experimental results available include the Pound-Rebka experiment and the detection of discrete bound states of neutrons in the gravitational field.
The above-mentioned experiments can be described in the context of non-relativistic quantum mechanics by using the gravitational potential for the potential term of the Schrödinger equation. Here, gravity is viewed as a classic (i.e. not quantized) field. A unification of gravity with the other three basic forces of physics , which are formulated in their most general form as quantum field theories , cannot be achieved in this way. The unification of quantum theory with general relativity is a current research topic; the current status is described in the article Quantum Gravity .
Applications
Quantum physical effects play an essential role in numerous applications of modern technology. Examples are the laser , the electron microscope , the atomic clock or, in medicine, imaging processes based on X-rays or nuclear magnetic resonance . The investigation of semiconductors led to the invention of the diode and the transistor , without which modern electronics would not exist. The concepts of quantum mechanics also play an essential role in the development of nuclear weapons .
In the invention or development of these and numerous other applications, however, the concepts and mathematical formalism of quantum mechanics are rarely used directly. As a rule, the more practical concepts, terms and rules of solid state physics, chemistry, materials science or nuclear physics are of greater practical importance. The relevance of quantum mechanics, on the other hand, results from the paramount importance that this theory has in the formulation of the theoretical foundation of many scientific disciplines.
Some examples of quantum mechanics applications are described below:
Atomic Physics and Chemistry
The chemical properties of all substances are a result of the electronic structure of the atoms and molecules that make them up. In principle, this electronic structure can be calculated quantitatively for all atomic nuclei and electrons involved by solving the Schrödinger equation. However, an exact analytical solution is only possible for the special case of hydrogen-like systems - that is, systems with an atomic nucleus and an electron. In more complex systems - i.e. in practically all real applications in chemistry or biology - the many-body Schrödinger equation can therefore only be solved using numerical methods . These calculations are very complex, even for simple systems. For example, the ab initio calculation of the structure and the infrared spectrum of propane with a commercially available PC took a few minutes in 2010, the corresponding calculation for a steroid took several days. For this reason, model simplifications and numerical methods for the efficient solution of the Schrödinger equation play a major role in theoretical chemistry , and the development of corresponding methods has developed into an extensive discipline in its own right.
A highly simplified model that is particularly frequently used in chemistry is the orbital model . In this model, the many-particle state of the electrons of the atoms under consideration is formed by the sum of the single-particle states of the electrons. The model contains various approximations (among others: neglecting the Coulomb repulsion of the electrons among each other, decoupling the movement of the electrons from the nuclear movement), but allows an approximately correct description of the energy levels of the atom. The advantage of this model, in addition to the comparatively simple calculability, lies in the clear expressiveness of both the quantum numbers and the graphic representation of the orbitals.
The orbital model allows the classification of electron configurations according to simple rules of construction ( Hund's rules ). The rules for chemical stability ( octet rule or noble gas rule , magic numbers ) and the systematics of the periodic table of the elements can also be justified by this quantum mechanical model.
By linearly combining several atomic orbitals, the method can be extended to so-called molecular orbitals , whereby calculations are much more complex in this case, since molecules do not have spherical symmetry. The calculation of the structure and the chemical properties of complex molecules on the basis of approximate solutions of the Schrödinger equation is the subject of molecular physics . This area laid the foundation for the establishment of quantum chemistry or computational chemistry as a sub-discipline of theoretical chemistry .
Nuclear physics
The nuclear physics is another major area of application of quantum theory. Atomic nuclei are quantum systems composed of nucleons with a very complex structure. In their theoretical description - depending on the specific question - a number of conceptually very different core models are used, which are usually based on quantum mechanics or quantum field theory. Below are some important use cases of quantum mechanics in nuclear physics:
- Single-particle models assume that the nucleons can move freely within the atomic nucleus. The influence of the other nucleons is described by a mean nuclear potential. Examples: shell model , Fermigas model .
- Cluster models describe nuclei as aggregates of small nucleon clusters , especially alpha particles , which are characterized by a high binding energy. Alpha decay is one of the physical processes that can be explained with this model : Certain unstable nuclei, such as B. decay through the emission of alpha particles, whereby the decay probability can be quantum mechanically described by the tunnel effect .
- The quantum mechanical scattering theory is the basis for the calculation of scattering cross-sections , which enable a comparison of model calculations and the results of scattering experiments. A frequently used approximation method is Fermi's golden rule , which describes the transition rate (transition probability per time) from an initial state to another state under the influence of a disturbance.
Solid state physics
The large number of possible chemical compositions of condensed matter - i.e. of macroscopic matter in the solid or liquid state - and the large number of atoms that make up condensed matter are reflected in a large variety of material properties (see main article Matter ). Most of these properties cannot be described in the context of classical physics, while quantum mechanical models of condensed matter have proven to be extremely successful.
Due to the large number of particles involved, a direct solution of the Schrödinger equation for all microscopic components of a macroscopic piece of matter is impractical. Instead, models and solution methods are used that are adapted to the underlying type of material ( metal , semiconductor , ion crystal, etc.) and to the properties to be investigated. In the current models of condensed matter, atomic nuclei and electrons are the relevant basic building blocks of condensed matter. Here, atomic nuclei and internal electrons are usually combined to form an ion core , which greatly reduces the number of components and interactions to be taken into account in the model. Of the 4 basic forces of physics , only the electromagnetic interaction is taken into account, whereas gravity and the nuclear forces are irrelevant for the effects and energy scales considered in the physics of condensed matter.
Despite these simplifications, models of condensed matter are complex quantum mechanical many-body problems , with the consideration of the electron-electron interaction being a particular challenge. For many purposes, such as B. the calculation of the charge distribution , the phonon spectrum or the structural properties, the calculation of the electronic ground state is sufficient. In this case, the electronic many- particle problem can be reformulated as an effective single-particle problem using density functional theory or other methods, which today can also be routinely calculated for complex systems.
In addition to the ground state properties, the elementary excitations of condensed matter are often of interest. For example, all experimental methods of solid state spectroscopy are based on the principle that certain degrees of freedom of a sample are excited or de-excited by an external stimulus (e.g. light or neutrons) . The elementary excitations are collective quantum mechanical effects to which - similar to a free quantum object - an energy and a wavelength or a wave vector can be assigned, which is why they are also referred to as quasiparticles . Examples are the phonon (energy quantum of the lattice oscillation) or the exciton (electron-hole pair). Quasiparticles of different types can interact with one another and thus scatter one another or combine and form new quantum objects with properties that differ drastically from the properties of free electrons. A well-known example are the Cooper pairs , which according to the BCS theory enable the superconductivity of metals.
Quantum computing
The search for robust methods for the direct manipulation of quantum states is also of interest. For some years now, efforts have been made to develop a quantum computer which would work in a highly parallel manner by utilizing the various eigenstates and the probability nature of a quantum mechanical system. Such a quantum computer could be used, for example, to crack modern encryption methods . In return, with quantum cryptography, a system has been found for theoretically absolutely secure key exchange. In practice, this method is often slightly modified and less secure, since the transmission speed is also important here. One topic is quantum teleportation , which deals with the possibilities of transmitting quantum states over any distance.
reception
physics
| year | Surname | Reason for awarding the prize |
|---|---|---|
| 1932 |
Werner Heisenberg (awarded 1933) |
for the foundation of quantum mechanics, the application of the discovery of the allo- tropic forms of hydrogen has led |
| 1933 |
Erwin Schrödinger and PAM Dirac |
for the discovery of new productive forms of atomic theory |
| 1945 | Wolfgang Pauli | for the discovery of the exclusion principle known as the Pauli principle |
| 1954 | Max Born | "For his fundamental research in quantum mechanics, especially for his statistical interpretation of the wave function " |
Two years after the first publications, quantum mechanics had prevailed in the Copenhagen interpretation . The fifth Solvay conference in 1927 is an important milestone. Theory quickly acquired the status of a central pillar in the theoretical structure of physics . With regard to its performance in specific applications (but not with regard to its interpretation, see above ), quantum mechanics is practically undisputed to this day. Although there are a number of alternative, empirically non-equivalent theories, such as the family of dynamic collapse theories or the non-equilibrium versions of the De Broglie-Bohm theory , these theories have only marginal importance compared to quantum mechanics.
Several Nobel Prizes in Physics were awarded for the development of quantum mechanics :
In addition, there were a number of other Nobel Prizes for further developments and applications of quantum mechanics and for the discovery of effects that can only be explained in the context of quantum mechanics (see list of Nobel Prize winners for physics ). Several Nobel Prizes in Chemistry were awarded for successful applications of quantum mechanics, including the prizes to Robert Mulliken (1929, “for his fundamental work on the chemical bonds and the electronic structure of molecules using the orbital method”), to Walter Kohn (1998 , "For his development of quantum chemical methods") or to John Anthony Pople (1998, "for the development of methods with which the properties of molecules and their interaction in chemical processes can be theoretically researched").
Popular science presentations
Shortly after the establishment of quantum mechanics, various quantum physicists, z. B. Born, de Broglie, Heisenberg or Bohr, a series of semi-popular science books that dealt in particular with philosophical aspects of theory. In his book Mr. Tompkins Explores the Atom, the physicist G. Gamov illustrated the properties of quantum objects by letting his protagonists experience various adventures in a fictional quantum world. The Feynman lectures on physics published in 1964 , real textbooks but sensationally stimulating for the time, were also sold in large numbers. However, until the 1970s, publications on quantum mechanics by no means reached the level of public awareness that, for example, relativity theory and cosmology had. Furthermore, the practical effects of nuclear physics , especially the risks of nuclear weapons and nuclear energy, shaped the public discussion of modern physics.
In film and television, too, quantum mechanics was occasionally presented in a popular scientific form, e.g. B. in broadcasts by the physicist Harald Lesch .
Influence on popular culture, humanities and social sciences as well as appropriation by esotericism
With the advent of the New Age - counter-culture from the early 1970s, an increased interest in literature was created with borrowed from science expressions in the connections between quantum mechanics, the human consciousness and Far Eastern religion were produced. Books such as F. Capras Tao of Physics or G. Zukav's Dancing Wu Li Masters became bestsellers. Quantum mechanics - a key statement in these books - contains holistic and mystical implications that suggest a connection between spirituality , consciousness and physics to form an “organic” worldview.
From the 1980s onwards, the market for literature inspired by quantum mechanics experienced a further boom, and the word "quantum" developed into a buzzword used in many compound words . The published books covered a wide range of topics, ranging from easily understandable presentations to other books on the subject of "Quantum Mechanics and Consciousness" to topics such as "Quantum Learning", "Quantum Golf" or "Quantum Carrots". A well-known example of the expansion of quantum mechanical concepts to areas beyond their applicability is the film What the Bleep do we (k) now !? .
The literary scholar Elizabeth Leane comes to an ambivalent assessment of the genre. On the one hand, it attaches educational importance to the generally understandable presentation of science. On the other hand, she points out the problem of shifts in meaning that are generated through the use of metaphors and “fictional techniques”. Using the example of Zukav's Dancing Wu Li Masters , one of the best-selling and most frequently cited books that merge quantum mechanics and esotericism, she shows a rhetorical reinterpretation of quantum mechanics to support an anthropocentric worldview . The sociologist S. Restivo points out fundamental linguistic and conceptual problems in attempts to describe quantum mechanics colloquially and to combine it with mysticism. Many physicists, such as JS Bell , M. Gell-Mann or V. Stenger , reject hypotheses that establish connections between quantum mechanics and consciousness as speculative. The political scientist Alexander Wendt presented a new attempt in 2015 with the book Quantum Mind and Social Science .
art
Quantum mechanics was and is perceived and artistically processed in art , especially in fiction , but also in the fine arts and occasionally in theater .
The literary scholar E. Emter demonstrates traces of reception of quantum theory in texts by R. Musil ( The Man Without Qualities ), H. Broch , E. Jünger , G. Benn , Carl Einstein and B. Brecht , whereby her study focuses on the German-speaking area and limited to the years 1925 to 1970.
In recent years, works by sculptors depicting quantum objects as sculptures have attracted attention . The sculptor J. Voss-Andreae assumes that art that is not tied to the text form has possibilities for the representation of reality that are not available to science. One example is his sculpture Quantum Man (see illustration on the right), which commentators interpret as symbolizing the wave-particle dualism and the observer's perspective . Other well-known examples of artistic representations of quantum objects are the sculptures Quantum Corral and the Spin Family by the same artist and the Quantum Cloud by A. Gormley .
Some plays also deal with quantum mechanics, for example B. Tom Stoppard's play Hapgood or the play QED by the American playwright P. Parnell. In his play in Copenhagen , the writer M. Frayn translates Heisenberg's uncertainty principle into an uncertainty principle of human behavior.
literature
Standard textbooks
- Claude Cohen-Tannoudji : Quantum Mechanics. de Gruyter, 1999, ISBN 3-11-016458-2 .
- Richard Feynman : Feynman lectures on physics. Volume 3: Quantum Mechanics. Oldenbourg, 2007, ISBN 978-3-486-58109-6 .
- Torsten Fließbach : Quantum Mechanics: Textbook on Theoretical Physics III. Spectrum Academic Publishing House, 2008, ISBN 978-3-8274-2020-6 .
- Walter Greiner : Theoretical Physics. Volume 4: Quantum Mechanics - Introduction. Deutsch-Verlag, Frankfurt am Main 2005, ISBN 3-8171-1765-5 .
- Gernot Münster : Quantum Theory. De Gruyter, 2010, ISBN 978-3-11-021528-1 .
- Wolfgang Nolting : Basic course Theoretical Physics 5/1 (Quantum Mechanics - Basics) . Springer, 2008, ISBN 978-3-540-68868-6 .
- Wolfgang Nolting : Basic course Theoretical Physics 5/2 (Quantum Mechanics - Methods and Applications). Springer, 2012, ISBN 978-3-642-24420-9 .
Generally understandable introductions
- Tony Hey, Patrick Walters: The Quantum Universe. ISBN 3-8274-0315-4 .
- Anton Zeilinger : Einstein's Veil, The New World of Quantum Physics . Goldmann, 2003, ISBN 3-442-15302-6 .
- Silvia Arroyo Camejo : Quirky Quantum World . Springer, Berlin 2006, ISBN 3-540-29720-0 .
- Gert-Ludwig Ingold: quantum theory . CH Beck, Munich 2002, ISBN 3-406-47986-3 .
- Claus Kiefer: Quantum Theory . S. Fischer, Frankfurt am Main 2012, ISBN 978-3-596-19035-5 .
- Transnational College of Lex: What is Quantum Mechanics? A Physics Adventure . Language Research Foundation, Boston, 1996, ISBN 0-9643504-1-6 . (The book with 566 pages is part of a Japanese project in which scientific and linguistic knowledge - here English - is to be imparted at the same time.)
- John Gribbin, Friedrich Griese: In Search of Schrödinger's Cat: Quantum Physics and Reality. Piper Paperback, 2010, ISBN 978-3-492-24030-7 .
Applications
Atomic Physics and Theoretical Chemistry:
- EG Lewars: Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Springer, 2010, ISBN 978-90-481-3860-9 .
- A. Szabo, NS Ostlund: Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. Dover Publications, 1996, ISBN 0-486-69186-1 .
- PW Atkins , RS Friedman: Molecular Quantum Mechanics. 4th edition. Oxford University Press, Oxford 2004, ISBN 0-19-927498-3 .
- W. Kutzelnigg : Introduction to Theoretical Chemistry. Wiley-VCH, Weinheim 2002, ISBN 3-527-30609-9 .
- J. Reinhold: quantum theory of molecules. 3. Edition. Teubner, 2006, ISBN 3-8351-0037-8 .
Nuclear physics:
- B. Povh , K. Rith, C. Scholz, F. Zetsche, W. Rodejohann: Particles and nuclei: An introduction to physical concepts. 9th edition. Springer, 2014, ISBN 978-3-642-37821-8 .
- J. Bleck-Neuhaus: Elementary Particles: Modern Physics from Atoms to the Standard Model. 1st edition. Springer, 2010, ISBN 978-3-540-85299-5 .
Condensed Matter Physics:
- SG Louie, ML Cohen: Conceptual Foundations of Materials: A Standard Model for Ground- and Excited-State Properties. Elsevier, 2006, ISBN 0-444-50976-3 .
Quantum Computing:
- MA Nielsen, Isaac L. Chuang: Quantum Computation and Quantum Information. Cambridge University Press, 2000, ISBN 0-521-63503-9 .
Interpretations of quantum mechanics
- David Albert: Quantum Mechanics and Experience. Harvard University Press, Cambridge, MA 1992. At the same time, a very good and easily readable introduction with very simple models.
- Kurt Baumann, Roman U. Sexl : The interpretations of the quantum theory. (= Facets of Physics. Volume 11). 3rd, revised edition. Vieweg, Braunschweig 1987, ISBN 3-528-28540-0 . Critical considerations, supplemented with famous original treatises (in German translation) by Max Born , Werner Heisenberg , Albert Einstein , Niels Bohr , Erwin Schrödinger , Wladimir Fock , David Bohm , John Stewart Bell , Bryce DeWitt
- John Stewart Bell : Speakable and unspeakable in quantum mechanics . Cambridge University Press, Cambridge 1988. Bundles Bell's original essays; important for questions of interpretation u. a. the texts on Bohm's interpretation, for the most part rich in physical requirements
- Jeffrey Bub: Interpreting the Quantum World. Cambridge University Press, Cambridge 1997, ISBN 0-521-56082-9 .
- Jeffrey Bub: The Interpretation of Quantum Mechanics. Reidel, Dordrecht 1974, ISBN 90-277-0465-1 .
- Nancy Cartwright : Another Philosopher Looks at Quantum Mechanics, or: What Quantum Theory is Not. (PDF; 205 kB) Instrumentalist reaction to Putnam 2005: Quantum mechanics can remain uninterpreted as a “living and working theory”.
- Hong Dingguo: On the Neutral Status of QM in the Dispute of Realism vs. Anti-realism. In: Robert S. Cohen, Risto Hilpinen, Qiu Renzong (eds.): Realism and Anti-Realism in the Philosophy of Science. Kluwer Academic Publishers, Dordrecht 1996, ISBN 0-7923-3233-4 , pp. 307-316.
- Peter Forrest: Quantum metaphysics . Blackwell, Oxford 1988, ISBN 0-631-16371-9 . Discussion of realistic metaphysical options for interpretation
- Bas van Fraassen : Quantum Mechanics. An Empiricist View. Oxford University Press, Oxford 1991, ISBN 0-19-823980-7 Elaborated anti-realistic interpretation from the position of constructive empiricism
- RIG Hughes: The structure and interpretation of quantum mechanics . Harvard Univ. Pr., Cambridge, Mass. 1989, ISBN 0-674-84391-6 . At the same time, a full introduction to the theory that only requires school mathematics
- E. Joos et al. a .: Decoherence and the Appearance of a Classical World in Quantum Theory . Springer, Berlin 2003, ISBN 3-540-00390-8 . Detailed discussion of the classic borderline case and its relevance for the interpretation of quantum theory
- Tim Maudlin: Quantum Non-Locality and Relativity . Blackwell, Oxford U. K. / Cambridge MA 1994, ISBN 0-631-18609-3 .
- Hilary Putnam : A Philosopher Looks at Quantum Mechanics (Again). In: The British Journal for the Philosophy of Science. 56/4 (2005), pp. 615-634. Rejection of “Copenhagen” interpretations as mere rejection of scientific realism and statistical interpretation (Born), discussion of the most important remaining realistic options: spontaneous collapse (GRW) and Bohm
- Michael Redhead: Incompleteness, nonlocality and realism: a prolegomenon to the philosophy of quantum mechanics . Clarendon Press, Oxford 1987, ISBN 0-19-824937-3 . One of the most important advanced works, including a brief presentation of the theory
- Hans Reichenbach : Philosophic Foundations Of Quantum Mechanics. University Of California Press, 1944.
- Pieter E. Vermaas: A Philosopher's Understanding of Quantum Mechanics . Possibilities and Impossibilities of a Modal Interpretation. Cambridge University Press, 1999, ISBN 0-521-65108-5 . After a short introduction to the formalism similar to von Neumann, detailed presentation and discussion of different variants of modal interpretations, etc. a. van Fraassens, Bubs; Defending a variant of Dieks Cooking.
- John Archibald Wheeler (Ed.): Quantum theory and measurement. Princeton Univ. Press, Princeton, NJ 1983, ISBN 0-691-08315-0 . Standard manual with the most important texts from the history of interpretation, more extensive and more up-to-date than Sexl / Baumann.
Audios
- Herbert Pietschmann: Introduction to Quantum Mechanics . nerds_on_air, ORANGE 94.0.
Videos
- Robert Griffiths , Alain Aspect , Anton Zeilinger u. a .: Resources. Course material (videos, slides, handouts) iqc.uwaterloo.ca, accessed on July 24, 2012.
Web links
- Interactive experiments on quantum mechanics: quantum randomness, interference of individual quanta, entanglement, cryptography etc. ( flash plug-in required) - from the Friedrich-Alexander-Universität Erlangen-Nürnberg
- Olga Teider: Introduction to quantum theory with interactive experiments ( flash plugin required) - from Ulm University
- Jenann Ismael: Quantum Mechanics. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
- Thomas Neusius / Christian Ströbele: Quantum , Mathematics and Philosophy of a Physical Idea Course material, starting at school level
- Georg Bernhardt: Exam questions on quantum mechanics. PDF, German, 336 kB.
- Anton Zeilinger: On the Interpretation and Philosophical Foundation of Quantum Mechanics. (PDF; 62 kB) In: U. Ketvel u. a. (Ed.): Vastakohtien todellisuus. Festschrift for KV Laurikainen. Helsinki University Press, 1996.
- Nobel laureate in physics Theodor W. Hänsch on quantum mechanics, its fundamentals, development, applications, interpretations Interview, July 22, 2008
- A collection of the most philosophically significant experiments in quantum physics, simply explained ( Memento from February 1, 2015 in the Internet Archive )
- Quantum mechanics - the dream from which substances are generally understandable overview of the interpretations of quantum mechanics, September 2015
Individual evidence
- ^ See Max Planck: The origin and development of the quantum theory . The Clarendon press, Oxford 1922; Armin Hermann: From Planck to Bohr - the first fifteen years in the development of quantum theory. In: Angewandte Chemie . Vol. 82, No. 1, 1970, pp. 1-7, ISSN 0044-8249 ; Cathryn Carson: The Origins of the Quantum Theory (PDF; 376 kB). In: Beam Line. (Stanford Linear Accelerator Center). Volume 30, No. 2, 2000, pp. 6-19.
- ^ L. de Broglie: Recherches sur la théorie des Quanta . PhD thesis. English translation (translated by AF Kracklauer): In: Ann. de Phys. 10th Series, Volume III, 1925.
- ^ W. Heisenberg: About quantum theoretical reinterpretation of kinematic and mechanical relationships. In: Journal of Physics. Volume 33, 1925, pp. 879-893, doi: 10.1007 / BF01328377 .
- ↑ M. Born, P. Jordan: To quantum mechanics. In: Journal of Physics. Volume 34, 1925, pp. 858-888, doi: 10.1007 / BF01328531 .
- ↑ M. Born, W. Heisenberg, P. Jordan: To Quantenmechanik II. In: Zeitschrift für Physik. Volume 35, 1926, pp. 557-615, doi: 10.1007 / BF01379806 .
- ↑ E. Schrödinger: Quantization as an eigenvalue problem I. In: Annalen der Physik . Volume 79, 1926, pp. 361-376, doi: 10.1002 / andp.19263840404 ; E. Schrödinger: Quantization as an eigenvalue problem II. In: Annalen der Physik. Volume 79, 1926, pp. 489-527, doi: 10.1002 / andp.19263840602 ; E. Schrödinger: Quantization as an Eigenvalue Problem III. In: Annals of Physics. Volume 80, 1926, pp. 437-490, doi: 10.1002 / andp.19263851302 ; E. Schrödinger: Quantization as an eigenvalue problem IV. In: Annalen der Physik. Volume 81, 1926, pp. 109-139, doi: 10.1002 / andp.19263861802 .
- ↑ E. Schrödinger: About the relationship between Heisenberg-Born-Jordan quantum mechanics and mine. In: Annals of Physics. Volume 79, 1926, pp. 734-756, doi: 10.1002 / andp.19263840804 .
- ^ PAM Dirac: Principles of Quantum Mechanics. 4th edition. Oxford University Press, 1958, ISBN 0-19-851208-2 .
- ↑ John von Neumann: Mathematical foundations of quantum mechanics. 2nd Edition. Springer, Berlin 1996, Engl. (Authorized) edition (transl. RT Beyer): Mathematical Foundations of Quantum Mechanics . Princeton Univ. Press, 1955 (there p. 28ff.)
- ↑ In the mathematical sense, spectral values of an operator with a continuous spectrum, such as B. of the position or the momentum operator, no actual eigenvalues due to the lack of standardization. In physics textbooks, however, the convention generally applies that spectral values of a continuous spectrum are also referred to as eigenvalues. This article subscribes to this Convention. See e.g. BP Reineker u. a .: Theoretical Physics III: Quantum Mechanics 1. Volume 3, 2007, p. 124. Page no longer available , search in web archives: (google books)
- ^ A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, H. Ezawa: Demonstration of single-electron build-up of an interference pattern. In: American Journal of Physics. Volume 57, 1989, pp. 117-120, doi: 10.1119 / 1.16104 .
- ^ A. Einstein, B. Podolsky, N. Rosen: Can quantum-mechanical description of physical reality be considered complete? In: Physical Review . Volume 47, 1935, pp. 777-780, doi: 10.1103 / PhysRev.47.777 .
- ↑ JS Bell: On the Einstein Podolsky Rosen paradox. In: Physics. 1 # 3, 1964, p. 195.
- ↑ A. Aspect et al. a .: Experimental Tests of Realistic Local Theories via Bell's Theorem. In: Physical Review Letters. Volume 47, 1981, p. 460, doi: 10.1103 / PhysRevLett.47.460 ; A. Aspect et al. a .: Experimental Realization of Einstein-Podolsky-Rosen-Bohm Thought Experiment: A New Violation of Bell's Inequalities. In: Physical Review Letters. Volume 49, 1982, p. 91, doi: 10.1103 / PhysRevLett.49.91 ; A. Aspect et al. a .: Experimental Test of Bell's Inequalities Using Time-Varying Analyzers. In: Physical Review Letters. Volume 49, 1982, p. 1804, doi: 10.1103 / PhysRevLett.49.1804 ; MA Rowe, D. Kielpinski, V. Meyer, CA Sackett, WM Itano, C. Monroe, DJ Wineland: Experimental violation of Bell's inequalities with efficient detection. In: Nature . Volume 409, 2001, pp. 791-794, doi: 10.1038 / 35057215 .
- ^ M. Schlosshauer: Decoherence and the Classical-to-Quantum Transition. At: books.google.de. Springer, 2007, p. 7.
- ↑ Omnes estimates the decoherence time for a pendulum with a mass of 10 g to be τ d = 1.6 · 10 −26 s. See R. Omnes: Understanding Quantum Mechanics. Princeton University Press, 1999, p. 202 and p. 75.
- ^ F. Wilczek: Quantum Field Theory. In: Compendium of Quantum Physics. Springer, 2009, p. 549 ff.
- ↑ The grouping in instrumentalism versus realism is a strong simplification of the actually existing variety of different positions of the philosophy of science . A detailed overview of the most important epistemological positions in physics can be found, for example, in Bernard d'Espagnat : Reality and the Physicist . Cambridge University Press, 1989.
- ↑ HP Stapp: The Copenhagen Interpretation. In: American Journal of Physics. Volume 40, 1972, p. 1098.
- ↑ In the English-language literature there are a number of different terms for the definition of values: “value-definiteness”, “intrinsic property”, “pre-assigned initial values” (Home and Whitaker), “precise value principle” (Hughes), “classical principle C ”(Feyerabend), as well as Bell's“ beables ”. The concept of " true value " used in measurement technology also requires a definition of value.
- ↑ There are different views on the epistemological classification of value definition. Feyerabend called it a “classical principle”, and d'Espagnat assigned it to physical realism . For the physicist T. Norsen, on the other hand, the principle of value definition cannot be assigned to any of the common realistic positions of epistemology, which is why he rejects the use of the term “realism” in this context: T. Norsen: Against 'realism'. In: Foundations of Physics. Vol. 37, 2007, p. 311. (online)
- ^ AO Bolivar: Quantum-Classical Correspondence: Dynamical Quantization and the Classical Limit. Springer, 2004, chap. 5. (google books)
- ^ AJ Makowski: A brief survey of various formulations of the correspondence principle. In: Eur. J. Phys. 2006, 27, pp. 1133-1139.
- ^ M. Schlosshauer, Decoherence and the Classical-to-Quantum Transition. Springer, 2007, p. 8. (google books)
- ^ NP compatriot: Between Classical and Quantum. In: Handbook of the Philosophy of Science: Philosophy of Physics Part A. Elsevier, 2007, p. 417 ff and p. 515 ff. (Google books)
- ^ AJ Leggett: Realism and the physical world. In: Rep. Prog. Phys. 2008, 022001.
- ↑ a b V. V. Nesvizhevsky, KV Protasov: Quantum states of neutrons in the earth's gravitational field: state of the art, applications, perspectives. In: Trends in quantum gravity research. Nova Science, 2006, p. 65. (google books)
- ↑ T. Jenke: Realization of a gravity-resonance-spectroscopy technique. In: Nature Physics . 7, 2011, p. 468. (online)
- ↑ EC Lewars: Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Springer, 2010, p. 2. (google books)
- ^ "[...] our understanding of the nucleus itself is seemingly quite incomplete. More than 30 nuclear models - based on strikingly different assumptions - are currently employed. Each provides some insight into nuclear structure or dynamics, but none can claim to be more than a partial truth, often in conflict with the partial truths offered by other models. "In: ND Cook: Models of the Atomic Nucleus. Springer, 2006, p. 5.
- ↑ An important exception is the droplet model , an empirical formula for calculating the binding energy of atomic nuclei.
- ^ Klaus Bethge : Nuclear Physics. Springer, 1996, ISBN 3-540-61236-X .
- ^ SG Louie, ML Cohen: Conceptual Foundations of Materials: A Standard Model for Ground and Excited State Properties. Elsevier, 2006. (google books)
- ↑ a b Michael A. Nielsen, Isaac L. Chuang: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge 2000, ISBN 0-521-63503-9 .
- ↑ S. Olmschenk, DN Matsukevich, P. Maunz, D. Hayes, L.-M. Duan, C. Monroe: Quantum Teleportation between Distant Matter Qubits. In: Science. 323: 486 (2009).
- ↑ "In an amazingly short period the Copenhagen interpretation gained ascendancy as the correct view of quantum phenomena." JT Cushing: Quantum Mechanics: Historical Contingency and the Copenhagen Hegemony. Univ. of Chicago Press, 1994, chap. 7.2. (google books)
- ↑ "But for GRW to move beyond being regarding as a set of interesting ideas, and to be taken fairly seriously as a genuine alternative to the standard theory, it is also essential that it makes some predictions clearly at variance with regular quantum theory that may then be checked experimentally. "A. Whitacker: The New Quantum Age: From Bell's Theorem to Quantum Computation and Teleportation. Oxford University Press, 2011, p. 258. (google books)
- ^ A b E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, p. 28. (google books)
- ^ "[…] He developed the Feynman Lectures on Physics, which have sold over a million copies and are still widely read today." In: Encyclopedia of Science and Technology Communication. Sage Pubn, 2010, p. 299. (google books)
- ^ A b E. Leane, Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, p. 31 ff. (Google books)
- ^ E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, p. 32 ff. (Google books)
- ^ F. Capra: The Tao of Physics. Shambhala Publications, 1975, p. 54, p. 140, chap. 18th
- ^ A b E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, p. 34. (google books)
- ^ E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, p. 86 ff and p. 4. (google books)
- ^ E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, pp. 95-96. (google books)
- ^ E. Leane: Reading Popular Physics: Disciplinary Skirmishes and Textual Strategies. Ashgate Publishing, 2007, pp. 104/105. (google books)
- ^ Sal Restivo: The Social Relations of Physics, Mysticism and Mathematics. Springer, 1985, chap. 2. (google books)
- ↑ JS Bell: Speakable and unspeakable in quantum mechanics. 2nd Edition. Cambridge University Press, 2004, p. 170. (google books)
- ↑ “While many questions about quantum mechanics are still not fully resolved, there is no point in introducing needless mystification where in fact no problem exists. Yet a great deal of recent writing about quantum mechanics has done just that. "In: Murray Gell-Mann: The Quark and the Jaguar: Adventures in the Simple and the Complex. Owl Books, 2002, chap. 12 Quantum Mechanics and Flapdoodle .
- ^ VJ Stenger: Quantum Gods: Creation, Chaos, and the Search for Cosmic Consciousness. Prometheus Books, 2009.
- ↑ Alexander Wendt: Quantum Mind and Social Science - unifying physical and social ontology . Cambridge University Press, Cambridge (England) 2015, ISBN 978-1-107-44292-4 .
- ↑ E. Emter: Literature and Quantum Theory. The reception of modern physics in writings on the literature and philosophy of German-speaking authors (1925–1970). de Gruyter, 1995, chap. 3.2 (google books) .
- ↑ A. Schirrmacher, review of E. Emter's book Literature and Quantum Theory. The reception of modern physics in writings on the literature and philosophy of German-speaking authors (1925–1970). In: H-SOZ-U-KULT. 1997. Online article (accessed January 4, 2012) .
- ^ S. Farr: Sculpture show takes steps in right direction. ( Memento of September 29, 2007 in the Internet Archive ). Retrieved January 4, 2012.
- ↑ a b c P. Ball: Worlds Within Worlds: Quantum Objects by Julian Voss-Andreae. In: Nature. 462, 2009, p. 416. Online article (fee required) .
- ^ D. Vanderbeke: Routledge Companion to Literature and Science. Taylor & Francis, 2010, p. 198. (google books)
- ↑ G. Bar-On: Copenhagen. In: The Columbia Encyclopedia of Modern Drama. 2007, p. 288. (google books)





































![\ vert \ Psi (x) \ vert ^ 2 = \ vert [\ psi_1 (x) + \ psi_2 (x)] \ vert ^ 2](https://wikimedia.org/api/rest_v1/media/math/render/svg/db63217de067b678a01a08e7e481efcb32c1a2d2)