Phase space

The phase space describes the set of all possible states of a dynamic system . A state is clearly represented by a point in the phase space. In mechanics it consists of generalized coordinates ( configuration space ) and associated generalized speeds (see principle of virtual power ).

Bulk

With degrees of freedom (number of generalized coordinates or spatial coordinates) the phase space is -dimensional. For example, a gas particle has degrees of freedom in three-dimensional space , with the associated impulses these are phase space coordinates. A system (gas) of particles has a -dimensional phase space. However, phase spaces in other applications outside of mechanics are also examined. ${\ displaystyle n}$ ${\ displaystyle 2n}$ ${\ displaystyle n = 3}$ ${\ displaystyle 6}$ ${\ displaystyle N}$ ${\ displaystyle 6N}$

The temporal development of a point in phase space is described by differential equations and represented by trajectories (trajectories, orbit) in phase space. These are differential equations of the first order in time and are clearly defined by a starting point (if the differential equation is independent of time, these are autonomous differential equations ). Accordingly, two trajectories do not cross in the phase space either, since the further course is not unambiguous at a crossing point. Closed curves describe oscillating (periodic) systems.

Construction of a phase (space) portrait for a mathematical pendulum

For systems with up to three variables, the phase space can be displayed graphically. For two variables in particular, the movement (trajectories, phase space flow as a vector field ) can be clearly represented in a phase space portrait or phase portrait and analyzed qualitatively ( phase space analysis , zero lines and fixed points ).

The historical origin of the use of phase spaces is often traced back to Joseph Liouville - because of the Liouville theorem (1838) that in conservative systems (with energy conservation) the phase space volume of neighboring trajectories is constant over time. However, Liouville did not have a mechanical system in mind, but proved the theorem for general, ordinary differential equations of the first order; the connection to mechanics was first suggested by Carl Gustav Jacobi . The phase space concept emerged only after the geometers had switched to the consideration of higher-dimensional spaces in the further course of the 19th century and the first use of phase space in today's sense was by Ludwig Boltzmann in 1872 as part of his investigations into statistical mechanics , which was adopted by James Clerk Maxwell in 1879 has been. The concept was then used in the lectures by Boltzmann and Josiah Willard Gibbs on statistical mechanics, in the article on statistical mechanics in the Encyclopedia of Mathematical Sciences from 1911 by Paul Ehrenfest and Tatjana Ehrenfest (who introduced the term for the phase space) and in qualitative Theory of differential equations by Henri Poincaré . ${\ displaystyle \ Gamma}$

A dynamic system, the trajectories of which fill the entire phase space, i.e. come as close as desired to any point in the phase space, is called ergodic , see also ergodic hypothesis . In conservative mechanical systems (closed systems), according to Liouville's theorem, the phase space volume of neighboring trajectories is constant over time, in dissipative systems it decreases (open systems).

In Hamiltonian mechanics, phase space is an example of a symplectic geometry and Hamiltonian mechanics, according to Vladimir Arnold, is the geometry of phase space . Since the impulses are defined as derivatives of the Hamilton function according to the generalized coordinates, the phase space there is a cotangential bundle over the configuration space.

In quantum mechanics, Heisenberg's uncertainty principle expresses a quantization of the phase space. In the older quantum theory, this is done using Bohr-Sommerfeld quantization . Transitions from distribution functions from classical to quantum mechanical phase space (and vice versa) are provided by the Wigner function and Weyl quantization .

Example of a phase space analysis

Phase portrait of the damped spring-mass oscillator with vector field and trajectory

Phase portrait of the Van der Pol oscillator with vector field and typical trajectories

Phase space of a plane pendulum with the angle on the x-axis and the angular velocity on the y-axis. The phase space is periodic with period with respect to the angle . The fixed point is stable, the fixed point is unstable. The separatrix, which separates the area of the "back and forth" pendulum movements (circular movement around the stable fixed point) from the upper and lower area of the continuous right and left rotations, is shown as a red line.

{\ displaystyle \ theta}

{\ displaystyle \ omega = {\ dot {\ theta}}}

{\ displaystyle \ theta}

{\ displaystyle 2 \ pi}

{\ displaystyle x_ {1}}

{\ displaystyle x_ {2}}

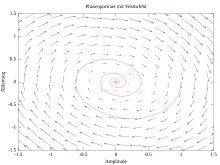
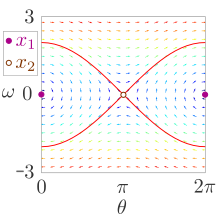
The phase space portrait gives the opportunity to graphically analyze the development of dynamic systems over time. For this, only the dynamic equations of the system are required; an explicit representation of the time development, e.g. by analytically solving a differential equation, is not necessary.

As an example, some elements of phase space analysis in a two-dimensional system , which are defined by the differential equations ( , ) ${\ displaystyle {x, y}}$ ${\ displaystyle x '= {\ frac {\ mathrm {d} x} {\ mathrm {d} t}}}$ ${\ displaystyle y '= {\ frac {\ mathrm {d} y} {\ mathrm {d} t}}}$

{\ displaystyle x '= f (x, y)}

{\ displaystyle y '= g (x, y)}

is described:

Drawing in the vector field of dynamics: For a grid of points, the direction of movement in phase space is shown by arrows. If you follow the arrow starting at a certain starting point, you come to a new point where you can repeat this procedure. Using the vector field, you can also draw typical trajectories into the phase space portrait, which help to assess the qualitative behavior of the development over time. In the van der Pol oscillator, for example, all trajectories converge towards a limit cycle , which can be illustrated using sample trajectories inside and outside the cycle. For simple dynamic systems, vector fields and sample trajectories can often be drawn by hand; for more complex systems, this can be done using computer programs.

Drawing in the zero lines: A zero line describes a curve in phase space along which one of the dynamic variables does not change. In the case of the above two-dimensional system, the x-zero kline is defined by the condition and the y-zero kline is defined by. These equations can often be solved for one of the variables even if the overall dynamics cannot be analytically integrated. ${\ displaystyle x '= f (x, y) = 0}$ ${\ displaystyle y '= g (x, y) = 0}$

Determining fixed points and their stability: As fixed points states are called, which over time will not change. Such fixed points correspond to the crossing points of the zero lines in the phase space. In the above two-dimensional system, this is explained by the fact that the condition is met at such a crossing point . A linear stability analysis can also determine whether trajectories in the vicinity of these points are attracted or repelled. ${\ displaystyle g (x, y) = f (x, y) = 0}$

Finding separatrices: A separatrix (derived from the Latin separare “to separate”) is a curve or ( hyper ) surface that separates phase space regions with different (long-term) behavior. For example, if there are two fixed points that attract trajectories, there may be a separatrix that separates the two catchment areas. With the locations and the stability of all fixed points or with the vector field of the dynamics , the separating matrices can be found in suitable cases without further calculations.

Individual evidence

↑ However, the case can arise that in the phase space portrait two curves intersect like the separatrix for a pendulum, but the intersection point is not reached when moving on trajectories of the system.
↑ David Nolte: The tangled tale of phase space. Physics Today, April 2010, p. 33.
↑ Boltzmann, Vienna. Ber., 66, 1872, p. 275.
^ Maxwell, Trans. Cambridge Phil. Soc., Vol. 12, 1879, p. 547.
^ Arnold: Mathematical methods of classical mechanics. Springer, 1989, p. 161.
^ Steven H. Strogatz, Nonlinear Dynamics And Chaos . Westview Press, 2000, ISBN 978-0-7382-0453-6 , pp. 159 .

literature

YS Kim, WW Zachary (Eds.): The physics of phase space. , Proc. First Int. Conf. Physics Phase Space, College Park, Maryland 1986, Lecture Notes in Physics 278, Springer, Berlin 1987, ISBN 3-540-17894-5 .
Cosmas K. Zachos: Quantum mechanics in phase space - an overview with selected papers. World Scientific, Singapore 2005, ISBN 978-981-238-384-6 .
V. Arnold: Mathematical methods of classical mechanics. Springer 1989.

Web links

State space. In: Scholarpedia.org. (English, including references).

[1] However, the case can arise that in the phase space portrait two curves intersect like the separatrix for a pendulum, but the intersection point is not reached when moving on trajectories of the system.

[2] David Nolte: The tangled tale of phase space. Physics Today, April 2010, p. 33.

[3] Boltzmann, Vienna. Ber., 66, 1872, p. 275.

[4] Maxwell, Trans. Cambridge Phil. Soc., Vol. 12, 1879, p. 547.

[5] Arnold: Mathematical methods of classical mechanics. Springer, 1989, p. 161.

[6] Steven H. Strogatz, Nonlinear Dynamics And Chaos . Westview Press, 2000, ISBN 978-0-7382-0453-6 , pp. 159 .