Autonomous differential equation

An autonomous differential equation or autonomous system is a type of ordinary differential equation that does not explicitly depend on the independent variable .

For example, is the differential equation for the harmonic oscillator

${\displaystyle y''(x)+\lambda \cdot y(x)=0.}$

autonomous, the Mathieusche differential equation

${\displaystyle y''(x)+[\lambda +\gamma \cos(x)]\cdot y(x)=0.}$

on the other hand not, since it depends explicitly on the independent variable (a parameter is periodically changed "from outside"). ${\displaystyle x}$

The independent variable often stands for time in applications.

definition

An ordinary differential equation

${\displaystyle y^{(n)}(x)=f\left(y(x),y'(x),\dotsc ,y^{(n-1)}(x),x\right)}$

is called an autonomous differential equation if the function does not explicitly depend on the independent variable , i.e. if ${\displaystyle f}$ ${\displaystyle x}$

${\displaystyle y^{(n)}(x)=f\left(y(x),y'(x),\dotsc ,y^{(n-1)}(x)\right)}$

applies to everyone in the domain. ${\displaystyle x}$

This -th order differential equation can also be written as a system of first-order differential equations - adding new variables to it ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle y_{i}\,(x)=y^{(i)}\,(x)}$ With ${\displaystyle i=1,\dotsc ,n-1}$

and

${\displaystyle y_{0}\,(x)=y\,(x)}$ (the function you are looking for)

${\displaystyle y_{1}\,(x)=y'\,(x)={\frac {dy_{0}}{dx}}}$

${\displaystyle y_{2}\,(x)=y^{(2)}\,(x)={\frac {dy_{1}}{dx}}}$

${\displaystyle \cdot \cdot \cdot }$

${\displaystyle y_{n-1}\,(x)={\frac {dy_{n-2}}{dx}}}$

${\displaystyle {\frac {dy_{n-1}}{dx}}=f(y_{0},y_{1},\dotsc ,y_{n-1})}$

a.

This results in a system of coupled differential equations for the functions sought. ${\displaystyle n}$ ${\displaystyle n}$

The system of differential equations can be interpreted geometrically as a system of the first order in an n -dimensional phase space given by : ${\displaystyle {\vec {y}}(x)=\left(y_{0}(x),y_{1}(x),\dots ,y_{n-1}(x)\right)}$

${\displaystyle {\frac {d{\vec {y}}}{dx}}={\vec {f}}({\vec {y}})}$

The differential equation determines the tangents of the solution curves in phase space. Such a system of coupled autonomous ordinary differential equations of the first order can also be specified directly in the applications. The fixed points at which the derivative disappears are important for the qualitative discussion (see below).

The solutions of the autonomous differential equations are translation invariant . If there is a solution to an autonomous differential equation, then there is also a solution to this equation for all of them with a suitably shifted initial condition. ${\displaystyle y(x)}$ ${\displaystyle y(x+c)}$ ${\displaystyle c\in \mathbb {R} }$

In many applications the independent variable is time . ${\displaystyle t}$

A non-autonomous system in variables , in which still explicitly depends on the independent variable , can be created by adding another variable with ${\displaystyle n}$ ${\displaystyle y,y_{1},\dotsc ,y_{n-1}}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle y_{n}}$

${\displaystyle {\frac {dy_{n}}{dx}}=1}$

make formally autonomous. So you get

${\displaystyle {\frac {dy_{n-1}}{dx}}=f(y,y_{1},\dotsc ,y_{n-1},y_{n})}$.

Solution methods

The first order equation (the independent variable is below ) ${\displaystyle t}$

${\displaystyle {\frac {dx}{dt}}=f(x)}$

can be solved by separating the variables , formally:

${\displaystyle dt={\frac {dx}{f(x)}}}$

${\displaystyle t+C=\int {\frac {dx}{f(x)}}}$

with a constant . In the case of equations of the second order, as above, after introducing new variables, one can also solve by separating the variables. Be ${\displaystyle C}$

${\displaystyle {\frac {d^{2}x}{dt^{2}}}=f\left(x,{\frac {dx}{dt}}\right)}$

with the new variable

${\displaystyle v={\frac {dx}{dt}}\,\,\,}$ (Equation 1)

and

${\displaystyle {\frac {d^{2}x}{dt^{2}}}={\frac {dv}{dt}}={\frac {dx}{dt}}{\frac {dv}{dx}}=v{\frac {dv}{dx}}}$

you get:

${\displaystyle v{\frac {dv}{dx}}=f(x,v)\,\,\,}$ (Equation 2)

That is a coupled system of two equations (equation 1,2). If one applies the separation of the variables in equation 1, one obtains:

${\displaystyle t+C_{1}=\int {\frac {dx}{v(x)}}}$

For one has to solve equation 2. Is ${\displaystyle v(x)}$

${\displaystyle f(x,v)=f(x)}$

you can also separate the variables there and get:

${\displaystyle {\frac {v^{2}}{2}}+C_{2}=\int f(x)dx}$

and in total:

${\displaystyle t+C_{1}=\pm \int {\frac {dx}{\sqrt {2\int f(x)dx-2\,C_{2}}}}}$

Also with separation of the variables one can use the case:

${\displaystyle f(x,v)=v^{n}\,f(x)}$

treat, as seen by plugging into Equation 2.

Examples

Autonomous systems often appear in the theory of dynamic systems . An example of an autonomous differential equation is the logistic differential equation used in theoretical biology and the Lorenz attractor in chaos theory . Both are non-linear. In Hamiltonian mechanics (with the classical phase space of position and momentum variables) one has to do with such systems if the Hamilton function is not explicitly time-dependent.

Qualitative theory of the fixed points of the differential equation

The fixed point (equilibrium point) of the differential equation, viewed as a vector field (flow) in phase space (the tangents of the trajectories (orbits) are ) is a point at which the autonomous ordinary differential equation (the independent variable is time t, a subscript represents a Derivative ) has a zero: ${\displaystyle {\vec {x}}_{t}(t)}$ ${\displaystyle {\vec {x}}_{f}}$

${\displaystyle {\vec {x}}_{t}={\vec {f}}({\vec {x}})=0}$

Asymptotically stable fixed point: sink

At this point the dynamic system is stationary (independent of time). A fixed point is stable if trajectories from an area around the fixed point remain in the area, and asymptotically stable if trajectories from a surrounding area (the maximum extension is the basin of attraction of the fixed point) converge towards the fixed point, a case which often occurs with problems with attenuation. This is an example of an attractor. There are also more complicated attractors, for example with a limit cycle , only those of the type isolated points are considered here. ${\displaystyle t\to \infty }$

Linearize around the fixed point ${\displaystyle {\vec {f}}({\vec {x}})}$

${\displaystyle {\vec {u}}={\vec {x}}-{\vec {x}}_{f}}$:

${\displaystyle {\vec {u}}_{t}=A\cdot {\vec {u}}+{\vec {g}}({\vec {u}})}$

with higher order terms in , which are neglected, and a matrix , the Jacobi matrix : ${\displaystyle {\vec {g}}({\vec {u}})}$ ${\displaystyle A}$

${\displaystyle A=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)\,\,}$(evaluated at the point ) ${\displaystyle {\vec {x}}={\vec {x}}_{f}}$

so that the case is a constant matrix assumed to be non-singular . For the sake of simplicity, only the flat case is treated here . Then , since the matrix is real, it has the two complex conjugate eigenvalues , which are determined from the characteristic equation : ${\displaystyle {\vec {x}}=\left(x_{1},x_{2}\right)}$ ${\displaystyle A}$ ${\displaystyle \lambda _{1},\lambda _{2}}$

Neutral stability: periodic movement around a center, elliptical fixed point

${\displaystyle \operatorname {det} (\lambda -A)={\lambda }^{2}-\lambda \,\operatorname {Sp} (A)+\operatorname {det} (A)=0}$

${\displaystyle \lambda _{1,2}={\frac {1}{2}}\left(\operatorname {Sp} (A)\pm {\sqrt {{(\operatorname {Sp} (A))}^{2}-4\,\operatorname {det} (A)}}\right)}$

expressed by the determinant and trace of the matrix . The solution to the linearized equation is: ${\displaystyle \operatorname {det} (A)=\lambda _{1}\cdot \lambda _{2}}$ ${\displaystyle \operatorname {Sp} (A)=\lambda _{1}+\lambda _{2}}$ ${\displaystyle A}$

${\displaystyle {\vec {u}}(t)=\sum _{i=1,2}u_{i}(0){\vec {e_{i}}}e^{\lambda _{i}\,t}}$

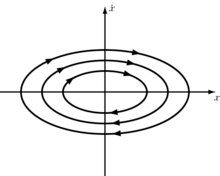
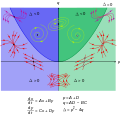
• The case of asymptotic stability (figure on the right) then exists for (both eigenvalues ​​negative real part ). This corresponds exactly to the case that and in the phase image there is a sink (stable node). In the figure it has a spiral shape (that is, the eigenvalues ​​are not real, but do not have a vanishing imaginary part), which is also called focus, if they are real there is a node. ${\displaystyle \operatorname {Re} (\lambda _{i})<0}$ ${\displaystyle \operatorname {det} (A)>0}$ ${\displaystyle \operatorname {Sp} (A)<0}$

• For (i.e. purely imaginary eigenvalues) one has the case of neutral stability, for example the periodic movement of a pendulum (the phase image has a center manifold, elliptical fixed point). That corresponds to that . ${\displaystyle \operatorname {Re} (\lambda _{i})=0}$ ${\displaystyle \operatorname {Sp} (A)=0}$

• If is for only one of the eigenvalues , all eigenvalues ​​are real and the second eigenvalue is positive. That corresponds to the case . Here you have a saddle point . The phase space of the differential equation is divided into four areas at the saddle point by two crossing straight lines (separatrix), in which the trajectories remain. On one straight line the path runs for to the fixed point (stable submanifold), on the other it runs away from the fixed point (unstable submanifold), i.e. for to the fixed point. Since they only reach the fixed points for infinite times, the trajectories belonging to the straight lines do not intersect. ${\displaystyle \operatorname {Re} (\lambda _{1})<0}$ ${\displaystyle \lambda _{2}}$ ${\displaystyle \operatorname {det} (A)<0}$ ${\displaystyle t\to \infty }$ ${\displaystyle t\to -\infty }$

Saddle point

• For one does not have a stable fixed point: the trajectories strive away from the point. Here there is an unstable node ( source ) or, if the imaginary part of the eigenvalues ​​does not vanish, an unstable focus. That corresponds to the case and . ${\displaystyle \operatorname {Re} (\lambda _{i})>0}$ ${\displaystyle \operatorname {det} (A)>0}$ ${\displaystyle \operatorname {Sp} (A)>0}$

The discussion for the linearized case applies locally. For so-called hyperbolic fixed points, for which the real parts of the eigenvalues ​​of the linearized system are not equal to zero (which includes sources, sinks, saddle points and foci (spirals)), the linearized behavior can be used to infer the behavior of the nonlinear system near the fixed point ( Theorem von Hartman-Grobman ).

A distinction is made between conservative systems in which for the speeds ${\displaystyle {\vec {v}}={\vec {x}}_{t}}$

${\displaystyle \nabla {\vec {v}}=0}$

holds (e.g. Hamiltonian systems without time dependence of the Hamilton function according to Liouville's theorem ) and those in which this does not apply (dissipative systems). In conservative systems in which the phase space volume is preserved, there are only elliptical fixed points (centers) and saddle points (not sources, sinks or spirals) as fixed points, and limit cycles are also not permitted. Boundary cycles were first considered as possible boundary quantities of phase space flow by Henri Poincaré ( Poincaré-Bendixson 's theorem, which applies to two dimensions, makes statements about existence). Limit cycles can arise when the parameters of the system vary through Hopf bifurcation from fixed points (this corresponds to the case that and ). In a saddle-node bifurcation, two fixed points collide . This corresponds to the transition from to (from node to saddle points and vice versa). ${\displaystyle \operatorname {det} (A)\neq 0}$ ${\displaystyle \operatorname {Sp} (A)\to 0}$ ${\displaystyle \operatorname {det} (A)>0}$ ${\displaystyle \operatorname {det} (A)<0}$

In three dimensions one has three eigenvalues ​​and depending on their real and imaginary part vanish, positive or negative are more possibilities: for example, in addition to saddle and nodes as above, stable and unstable focus nodes and saddle foci. There are also new types of non-hyperbolic fixed points that are not structurally stable when the non-linear terms are added. Rather, their behavior depends on the non-linear terms and new types of non-hyperbolic fixed points arise, for example in the case of Hopf bifurcations or saddle-node bifurcations. For example, the Bogdanov-Takens bifurcation occurs in nonlinear systems in which two of the eigenvalues ​​vanish (it consists of a combination of the saddle-knot bifurcation and the Hopf bifurcation).

gallery

• 

  Qualitative behavior near the fixed points in two dimensions depending on track p and determinant q

• 

  Phase diagrams of the pendulum with a continuous blue separatrix with saddle points in the apparent intersections. The separatrix envelops the closed curves (periodic movement with center)

literature

• Günther Wirsching: Ordinary differential equations , Teubner 2006
• Hirsch, Smale, Devaney: Differential Equations, Dynamical Systems and Introduction to Chaos , Academic Press 2004

Individual evidence

1. ^ Autonomous, Wolfram Mathworld
2. ↑ Representation in the following from Beltrami, Mathematics for Dynamics Modeling, Academic Press 1987. Also represented in Hirsch, Smale, Differential Equations, Dynamical Systems and Linear Algebra, Academic Press 1974 and the new edition Hirsch, Smale, Devaney, Differential Equations, Dynamical Systems and Introduction to Chaos, Academic Press 2004, there classification of plane systems according to determinant and trace of the matrix summarized in the figure on p. 63
3. ^ Fixed points, spectrum lexicon of physics
4. ↑ Sometimes a saddle point is also called a hyperbolic fixed point in the narrower sense, the case of a center is called elliptical, see the spectrum lexicon of physics cited above.
5. ↑ See the illustrations in Eugene M. Izhikevich, Equilibrium, Scholarpedia