Harmonic oscillator

This article covers the harmonic oscillator in general. For the special case of quantum mechanics, see harmonic oscillator (quantum mechanics) .

A harmonic oscillator is a system that can vibrate and is characterized by a linear reset variable. For a mechanical system this means that there is a force that counteracts an increasing deflection with proportionally increasing strength. After an external impulse, a harmonic oscillator oscillates sinusoidally (= harmonic ) around its position of rest , the duration of the oscillation being independent of the size of the deflection. Examples of harmonic oscillators are spring pendulums , electrical oscillating circuits and tuning forks .

The harmonic oscillator is an important model system in physics. It is fully described by only two parameters , the natural frequency and the damping . Many more complex systems behave approximately like harmonic oscillators with small deflections, e.g. B. the thread pendulum . The harmonic oscillator in quantum mechanics is one of the few quantum mechanical systems that can be calculated without approximations.

The term harmonic oscillator is also used for damped harmonic oscillators , even if, strictly speaking, they do not carry out a harmonic oscillation, but a damped oscillation .

Differential equation of the harmonic oscillator

Mathematically, every free harmonic oscillator can be described by the following differential equation . Exceptions are oscillators in quantum mechanics and related theories, where uncertainty relations must be taken into account.

${\displaystyle {\ddot {x}}+\omega _{0}^{2}\,x=0}$

This includes the deflection of the system and the resonance frequency . It is an ordinary, linear , homogeneous differential equation of the second order, which can therefore easily be solved analytically. The solution to such an equation is a sinusoidal function. ${\displaystyle x(t)}$ ${\displaystyle \omega _{0}}$ ${\displaystyle x(t)}$

Harmonic oscillator potential

The potential V of a one-dimensional harmonic oscillator

The undamped harmonic oscillator is a conservative system. This means that the energy of the vibration is retained. There is therefore a potential for every oscillator force field .

One-dimensional oscillator

The graphic representation of the potential of a harmonic oscillator is a parabola . It is also called harmonic potential. ${\displaystyle V}$

${\displaystyle V(x)={\frac {1}{2}}kx^{2}}$with the benchmark ${\displaystyle k>0}$

In mechanics, the force on a particle in such a potential is given by the negative derivative of the potential. ${\displaystyle F}$

${\displaystyle F=-{\frac {\mathrm {d} V}{\mathrm {d} x}}=-kx}$

Multi-dimensional oscillator

The potential of a two-dimensional isotropic harmonic oscillator

This concept can be applied to several dimensions . The potential here has the shape of an elliptical paraboloid . In n dimensions, it can be a suitable choice of coordinates as write this:

${\displaystyle V(x_{1},\dotsc ,x_{n})={\frac {1}{2}}\sum _{i=1}^{n}k_{i}\,x_{i}^{2}}$

In mechanics, the force on a particle in such a potential is given by the negative gradient of the potential.

Because there are no mixed terms between different directions in the individual summands, the problem of an n -dimensional harmonic oscillator can be reduced to n one-dimensional oscillators. In quantum mechanics, such a property is called separability . It can be concluded that with a harmonic oscillator not only the total energy but also the energies for the components of each individual direction are conserved quantities.

If the value of the potential depends only on the distance to the zero point, but not on the direction, then the oscillator is called isotropic , otherwise anisotropic . With an isotropic oscillator all constants have the same value:

${\displaystyle k_{i}=c>0~~~~~~~~\forall i=1,\ldots ,n}$

and vibrations in each direction are harmonic and have the same frequency.

In an anisotropic oscillator, the vibrations are harmonic in a single coordinate and have a frequency that depends on (normal vibrations ). If several normal vibrations are excited with different ones , more complicated, possibly also non-periodic movements result. ${\displaystyle x_{i}}$ ${\displaystyle k_{i}}$ ${\displaystyle k_{i}}$

Minimum of potential

The minimum of this potential is a stable fixed point of the system. In mechanics, this point is also called the position of rest and the force that the particle experiences, the restoring or return force. In particular, a particle lying in the rest position experiences no force whatsoever, from which the name "rest position" is derived. The naming is somewhat misleading in this respect: Although no force acts on a particle in the rest position, the particle does not have to be at rest there. In general, it even assumes its maximum speed there.

Importance in physics

Quadratic approximation of the Lennard-Jones (12.6) potential. The variable x corresponds to the distance u .

An ideal harmonic oscillator, in which the restoring force for any large deflections increases linearly with the deflection, does not exist in nature. Nevertheless, the concept is of fundamental importance for physics, since often only small deflections of an object from the rest position are considered. If one restricts oneself to this, potentials that have a local minimum can be replaced to a good approximation by a harmonic potential and the entire problem can be described as a harmonic oscillator. The advantage of such a harmonic approximation is that the problem can be handled with standard methods of theoretical physics and provides analytical solutions that are easy to interpret. In the figure opposite, this was carried out for a Lennard-Jones (12.6) potential (blue curve). As can be seen, the result (red curve) is only a useful approximation for small distances from the minimum.

The harmonic approximation finds its mathematical justification in the fact that the potentials can be developed in a Taylor series . If a potential is given and if it is sufficiently often differentiable, then according to Taylor's theorem : ${\displaystyle V}$

${\displaystyle V(x)=V(x_{0})+{\frac {\partial V}{\partial x}}(x_{0})(x-x_{0})+{\frac {1}{2}}{\frac {\partial ^{2}V}{\partial x^{2}}}(x_{0})(x-x_{0})^{2}+R(x-x_{0})}$

where , the so-called remainder term, only contains terms from the third order. It is therefore negligible for small distances . As a development point we choose a minimum of the potential so that applies . The first-order term is therefore also omitted. For better mathematical manipulation can by a suitable coordinate transformation of the apex be added to the origin of coordinates, so that the following applies: . Furthermore, it is always possible to bet. The approximate harmonic potential is then obtained: ${\displaystyle R(x-x_{0})}$ ${\displaystyle x-x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle {\tfrac {\partial V}{\partial x}}(x_{0})=0}$ ${\displaystyle x_{0}=0}$ ${\displaystyle V(x_{0})=0}$

${\displaystyle V(x)={\frac {1}{2}}kx^{2}}$ With ${\displaystyle k={\frac {\partial ^{2}V}{\partial x^{2}}}(x_{0})}$

This means that if the deflection is sufficiently small, the oscillator behaves harmoniously. An example of oscillators that become anharmonic even at medium amplitudes is the thread pendulum .

An approximate solution method, in which a complicated problem is first reduced to an analytically solvable one, in order to then add previously ignored influences in the form of perturbations to the solution, is called perturbation theory .

The harmonic oscillator of classical mechanics

One-dimensional undamped oscillator

A mechanical oscillator consists of a body of mass and a force that drives it back when it is deflected from its rest position. In order for an oscillator to be harmonious, the restoring force must be proportional to this deflection, i.e. the distance of the body from its rest position. In practice, such a force is usually implemented by springs , as is the case with a spring pendulum , or by the weight of the body, as is the case, for example, with a water pendulum .

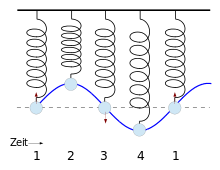
Description of the oscillation process

Representation of the oscillation of a harmonic oscillator using the example of a spring pendulum. The rest position of the oscillator is marked with a dashed line. The speed is marked as a red arrow

A harmonic oscillator is moved out of its rest position. The further you move it away, the greater the force trying to pull it back. The deflection adds potential energy to the oscillator . Potentially means that the energy is used to tension a spring, for example, and this energy is therefore stored in the position of the oscillator.

If the oscillator is then released, it is accelerated due to the tensile force of the spring. It therefore moves back to the rest position with increasing speed. When it gets there, the oscillator has reached its maximum speed. The spring is relaxed and there is no longer any force acting on the oscillator. The potential energy that was fed to it has now been completely converted into kinetic energy . This means that it is no longer stored in the position but in the speed of the oscillator.

However, due to inertia , the oscillator continues to move. This leads to the spring being tensioned again, this time in a different direction. To tension this spring, the oscillator has to use its kinetic energy in order to be able to move against the force of the spring. This slows it down until it reaches the point where it no longer moves and all of the energy is back in the form of potential energy. The sequence of movements then starts all over again.

time	Deflection ${\displaystyle x}$	potential energy ${\displaystyle {\frac {k}{2}}x^{2}}$	speed ${\displaystyle {\dot {x}}}$	kinetic energy ${\displaystyle {\frac {m}{2}}{\dot {x}}^{2}}$
1	${\displaystyle 0}$	${\displaystyle 0}$	${\displaystyle {\sqrt {2E/m}}}$	${\displaystyle E}$
2	${\displaystyle {\sqrt {2E/k}}}$	${\displaystyle E}$	${\displaystyle 0}$	${\displaystyle 0}$
3	${\displaystyle 0}$	${\displaystyle 0}$	${\displaystyle -{\sqrt {2E/m}}}$	${\displaystyle E}$
4th	${\displaystyle -{\sqrt {2E/k}}}$	${\displaystyle E}$	${\displaystyle 0}$	${\displaystyle 0}$
unchangeable: total energy , mass and spring constant ${\displaystyle E}$ ${\displaystyle m}$ ${\displaystyle k}$

Derivation of the oscillation equation

Illustration of the physical quantities of a spring pendulum. The force is shown as a green arrow

As above, we take a spring pendulum as an example. The mass of the body is . We take the rest position as the zero point and denote the deflection with . The force that acts on the body is described by Hooke's law : ${\displaystyle m}$ ${\displaystyle x}$ ${\displaystyle F}$

${\displaystyle F=-kx}$

The constant is a spring constant that depends on the strength of the restoring force in the case of a fixed deflection. It is also known that the acceleration of a body is proportional to the force acting on it. The acceleration can be written as the second derivative of the location in terms of time. A time derivative is often identified in physics as a point above the variable: ${\displaystyle k}$ ${\displaystyle x}$

${\displaystyle F=m{\ddot {x}}}$

If one now equates these two expressions for the force , one obtains a differential equation: ${\displaystyle F}$

${\displaystyle m{\ddot {x}}=-kx}$

To simplify the following calculations, substitute and rewrite the equation: ${\displaystyle \omega _{0}^{2}={\frac {k}{m}}}$

${\displaystyle {\ddot {x}}+\omega _{0}^{2}x=0}$

This equation can be solved using an exponential approach, for example . The result is a sinusoidal function, also called harmonic oscillation:

${\displaystyle x(t)=u\,\sin(\omega _{0}t+\varphi )}$.

The solution contains two constants, the amplitude and the phase shift angle . They are obtained according to the initial conditions . The amplitude stands for the maximum deflection of the oscillator and thus the energy of the oscillation. The phase shift angle determines the position and at the same time the speed that the body has at the time . ${\displaystyle u}$ ${\displaystyle \varphi }$ ${\displaystyle t=0}$

The sine function is a periodic function because its values ​​are repeated at regular intervals ( ). Therefore the oscillator performs a periodic movement. denotes the natural angular frequency and resonance frequency of the oscillator. It determines the frequency with which the oscillator oscillates. In the case of a harmonic oscillator, this frequency is independent of the oscillation amplitude. ${\displaystyle \sin(x)=\sin(x+2\pi )}$ ${\displaystyle \omega _{0}}$ ${\displaystyle f={\frac {\omega _{0}}{2\pi }}}$

energy

In the case of the free undamped oscillator, the energy is retained because it is a closed system and only conservative forces occur. In the equilibrium position, the potential energy disappears. Therefore the total energy is equal to the maximum kinetic energy:

${\displaystyle E_{\text{gesamt}}={\hat {E}}_{\text{kin}}={\frac {1}{2}}m{\hat {v}}^{2}={\frac {1}{2}}m\omega ^{2}{\hat {x}}^{2}}$

The same result is obtained if the total energy is calculated using the maximum value of the potential energy:

${\displaystyle E_{\text{gesamt}}={\hat {E}}_{\text{pot}}={\frac {1}{2}}k{\hat {x}}^{2}={\frac {1}{2}}m{\sqrt {\frac {k}{m}}}^{2}{\hat {x}}^{2}={\frac {1}{2}}m\omega ^{2}{\hat {x}}^{2}}$.

${\displaystyle {\hat {x}}}$stands here for the maximum value of the deflection, i.e. for the amplitude. If complex numbers are used for the calculation, the square of the magnitude of the amplitude, which may be complex , takes the place of . ${\displaystyle {\hat {x}}^{2}}$

One-dimensional damped oscillator

weak, linearly damped oscillation of a harmonic oscillator

A mechanical vibration is generally not frictionless. This means that the oscillation loses energy through friction and therefore its amplitude decreases. One speaks of a damping of the oscillation, whereby it is generally no longer harmonious. Such a system is no longer conservative , but dissipative . In the differential equation, a friction force F _{R is} added to the accelerating force F.

${\displaystyle m{\ddot {x}}(t)=-kx(t)+F_{\mathrm {R} }}$

The sign of the force is opposite to the speed. The exact expression for F _R depends on the type of friction. The magnitude of F can be constant or, for example, have a linear or quadratic dependence on the speed.

In the case of sliding friction , the amount of F _{R is} constant:

${\displaystyle F_{\mathrm {R} }=-d\operatorname {sgn} \left({\dot {x}}(t)\right)}$

An example of a linear dependence is the air friction at low speeds. There the air flow can be viewed as laminar . Thus, according to Stokes' law , it is proportional to the speed, i.e. to the first time derivative of the deflection.

${\displaystyle F_{\mathrm {R} }=-d{\dot {x}}(t)}$

In the case of such a linear damping, the proportionality factor is called the damping constant . ${\displaystyle d}$

Linear damping

See also : Linear damped oscillation

In the case of linear damping, the friction can generally be added by a damping term which is proportional and opposite to the speed . The constant is also known as the decay constant . This gives the equation of motion of a linearly damped oscillation as an ordinary linear differential equation of the second order: ${\displaystyle F_{\mathrm {R} }=-2m\gamma {\dot {x}}}$ ${\displaystyle {\dot {x}}}$ ${\displaystyle \gamma \geq 0}$

${\displaystyle {\ddot {x}}(t)+2\gamma {\dot {x}}(t)+\omega _{0}^{2}x(t)=0}$.

${\displaystyle \omega _{0}}$denotes the undamped natural angular frequency of the oscillator. An exponential approach leads to the general solution ${\displaystyle x(t)=e^{\lambda t}}$

${\displaystyle x(t)=e^{-\gamma t}\left(c_{1}e^{{\sqrt {\gamma ^{2}-\omega _{0}^{2}}}t}+c_{2}e^{-{\sqrt {\gamma ^{2}-\omega _{0}^{2}}}t}\right)}$

Where and are complex-valued constants that are determined from the initial conditions. ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$

• In the case of weak damping ( ), as in the undamped case, there is a sinusoidal oscillation, the amplitude of which, however, drops exponentially. The strength of this drop is determined by the exponent of the enveloping exponential function: The amplitude drops to the original amplitude over the period. The angular frequency of the oscillation decreases to . ${\displaystyle \gamma <\omega _{0}}$ ${\displaystyle \gamma }$ ${\displaystyle \tau =1/\gamma }$ ${\displaystyle 1/e}$ ${\displaystyle \omega _{d}={\sqrt {\omega _{0}^{2}-\gamma ^{2}}}}$
• In the case of strong damping ( ), the so-called creep case , no real oscillation develops. Rather , the deflection creeps towards the rest position. ${\displaystyle \gamma >\omega _{0}}$
• In the aperiodic limit case ( ), the oscillation still reaches a maximum deflection ( ), but then falls back to the rest position more quickly than in the case of strong damping. Whether a zero crossing takes place depends on the initial conditions. ${\displaystyle \gamma =\omega _{0}}$ ${\displaystyle t=\tau }$

If the initial conditions and the point in time are given, then in the case of oscillation the particulate solution is obtained ${\displaystyle x(0)}$ ${\displaystyle {\dot {x}}(0)}$ ${\displaystyle t=0}$ ${\displaystyle \omega _{0}^{2}-\gamma ^{2}>0}$

${\displaystyle x(t)=e^{-\gamma t}\left(x(0)\cdot \cos(\omega _{d}t)+\left(x(0)\cdot \gamma +{\dot {x}}(0)\right){\frac {\sin(\omega _{d}t)}{\omega _{d}}}\right)}$

With ${\displaystyle \omega _{d}^{2}=\omega _{0}^{2}-\gamma ^{2}}$

For the special case , d. H. without damping, the solution is simplified too ${\displaystyle \gamma =0}$

${\displaystyle x(t)=x(0)\cdot \cos(\omega _{0}t)+{\dot {x}}(0){\frac {\sin(\omega _{0}t)}{\omega _{0}}}}$

For the aperiodic borderline case results ${\displaystyle \omega _{0}^{2}-\gamma ^{2}=0}$

${\displaystyle x(t)=\left(\left({\dot {x}}(0)+\gamma \cdot x(0)\right)\cdot t+x(0)\right)e^{-\gamma t}}$

Variant: torsional oscillator

→ Main article : Torsion pendulum

The torsion oscillator is a variant of the classic harmonic oscillator. Instead of a helical spring, a torsion spring or a torsion thread is used here. Instead of translational movements, there are then rotational movements. In principle, the calculation is carried out in the same way. Only the mass is replaced by the moment of inertia and the speed by the angular velocity . ${\displaystyle m}$ ${\displaystyle I}$ ${\displaystyle v={\dot {x}}}$ ${\displaystyle \omega ={\dot {\varphi }}}$

Description in Hamilton dynamics

The undamped harmonic oscillator in phase space. Three trajectories with initial conditions of different energies are shown

The equation of motion of the harmonic oscillator can also be derived using Hamiltonian mechanics . As above, we consider a mass on a spring with spring constants . The generalized coordinate is used. The Hamilton function is made up of potential and kinetic energy as follows: ${\displaystyle m}$ ${\displaystyle k}$ ${\displaystyle x=q}$ ${\displaystyle H}$

${\displaystyle H={\frac {p^{2}}{2m}}+{\frac {m\omega _{0}^{2}q^{2}}{2}}}$

With the canonical equations

${\displaystyle {\dot {p}}=-{\frac {\partial H}{\partial q}}=-m\omega _{0}^{2}q}$

${\displaystyle {\dot {q}}={\frac {\partial H}{\partial p}}={\frac {p}{m}}}$

one arrives at the equation of motion already described above.

${\displaystyle {\ddot {q}}+\omega _{0}^{2}q=0}$

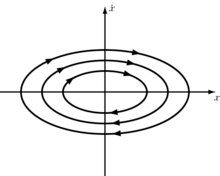
Since the total energy is preserved ( ), the position and momentum form an ellipse with semiaxes and . ${\displaystyle E}$ ${\displaystyle {\frac {\partial H}{\partial t}}=0}$ ${\displaystyle q}$ ${\displaystyle p}$ ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle {\frac {p^{2}}{2mE}}+{\frac {q^{2}}{2E/(m\omega _{0}^{2})}}=1={\frac {p^{2}}{a^{2}}}+{\frac {q^{2}}{b^{2}}}}$

The total energy of the system is proportional to the area enclosed by the ellipse ${\displaystyle A=\pi \cdot a\cdot b=2\pi E/\omega _{0}}$

In the case of a damped oscillator, instead of an ellipse , the trajectory forms a spiral that moves towards the origin.

In the case of a multidimensional harmonic oscillator, selections can be made by means of the principal axis transformation and along the principal axes of the potential. With such a choice, the equations of motion of the individual directions decouple. ${\displaystyle q_{i}}$ ${\displaystyle p_{i}}$

Multi-dimensional oscillator

Representation of the force field of an isotropic harmonic oscillator in two dimensions. The power is symbolized by red arrows. The rest position is marked as a blue point.

For example, with a Hamilton approach as explained in the previous section, the law of force for an n-dimensional harmonic oscillator can be formulated as:

${\displaystyle m{\ddot {\mathbf {x} }}=-\sum _{i=1}^{n}k_{i}\ x_{i}\,\mathbf {e} _{i}\,.}$

You can see that the differential equations are decoupled, i.e. the force component in one dimension only depends on the deflection in this dimension. Therefore the solutions for the individual components of the position vector are the solutions of the corresponding one-dimensional problem:

${\displaystyle x_{i}(t)=u_{i}\,e^{\lambda _{i}\,t}+v_{i}\,e^{-\lambda _{i}\,t}}$

The eigenvalues correspond to the eigencircle frequencies. If they can all be written as integer multiples of a constant, the oscillation of the harmonic oscillator is periodic. An isotropic harmonic oscillator is therefore always periodic. ${\displaystyle \textstyle \lambda _{i}=\mathrm {i} \,{\sqrt {\frac {k_{i}}{m}}}}$ ${\displaystyle \lambda _{i}}$

Two-dimensional oscillator

With an anisotropic two-dimensional harmonic oscillator, the particle moves on a Lissajous curve . The movement is periodic when the frequencies of the vibrations in one coordinate are in a rational relationship. Otherwise it is aperiodic, i.e. H. it never returns to the initial state. But it comes as close as you want to.

In the case of an isotropic two-dimensional harmonic oscillator, the Lissajous curve degenerates into a circle, a spatially fixed straight line or a spatially fixed ellipse. One example is the spherical pendulum with small deflections.

The equations of motion are

${\displaystyle {\begin{array}{ll}{\ddot {x}}&=-\omega _{0}^{2}\,x\\{\ddot {y}}&=-\omega _{0}^{2}\,y\end{array}}}$

The general solution can be written as:

${\displaystyle {\vec {r}}(t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}}\cos(\omega _{0}t)+{\begin{pmatrix}c_{3}\\c_{4}\end{pmatrix}}\sin(\omega _{0}t)}$,

where the constants are given by the starting location and the starting speed. In this case , the route is straight. If and and both are not parallel to each other, there are trajectories in the form of an ellipse or circle, the center of which is the rest position. ${\displaystyle {\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}}={\vec {r}}(0)}$ ${\displaystyle {\begin{pmatrix}c_{3}\\c_{4}\end{pmatrix}}={\vec {v}}(0)/\omega _{0}}$ ${\displaystyle {\vec {v}}(0)={\vec {0}}}$ ${\displaystyle {\vec {r}}(0)\neq {\vec {0}}}$ ${\displaystyle {\vec {v}}(0)\neq {\vec {0}}}$

To determine the possible forms of motion, the general solution is expressed as:

${\displaystyle {\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}A_{x}\,\cos(\omega _{0}t-\alpha _{x})\\A_{y}\,\cos(\omega _{0}t-\alpha _{y})\end{pmatrix}}}$

with arbitrary values ​​for the amplitudes and phase shifts that result from the initial conditions. Different trajectories can form, all of which have the origin as the center and are traversed with the same frequency: ${\displaystyle A_{x},\,A_{y}}$ ${\displaystyle \alpha _{x},\,\alpha _{y}}$

• For there is a linear harmonic oscillation between the points along a straight line that forms the angle with the x-axis . ${\displaystyle \alpha _{x}=\alpha _{y}}$ ${\displaystyle \textstyle \pm {\begin{pmatrix}A_{x}\\A_{y}\end{pmatrix}}}$ ${\displaystyle \arctan(\alpha _{y}/\alpha _{x})}$
• For there is an ellipse with the semi-axes of length or parallel to the coordinate axes. If so , the ellipse becomes a circle. Then the pendulum is a conical pendulum (see above). ${\displaystyle \alpha _{x},=0,\alpha _{y}=90^{\circ }}$ ${\displaystyle A_{x}}$ ${\displaystyle A_{y}}$ ${\displaystyle A_{x}=A_{y}}$
• In general, an ellipse results for any amplitude , the semi-axes of which depend on all four parameters and are inclined to the coordinate axes. ${\displaystyle \alpha _{x}\neq \alpha _{y}}$ ${\displaystyle A_{x},\,A_{y}}$

Complex number notation

The two coordinates can become a single complex variable

${\displaystyle u=x+{\text{i}}y}$

be summarized. The differential equation then applies to ${\displaystyle u}$

${\displaystyle {\ddot {u}}=-\omega _{0}^{2}\,u}$

with the general solution

${\displaystyle u(t)=A{\text{e}}^{\rm {{i}\omega _{0}t}}+B{\text{e}}^{-{\text{i}}\omega _{0}t}}$.

The two constants are calculated from the initial conditions: ${\displaystyle A,\,B}$

${\displaystyle {\begin{array}{ll}u(0)=x(0)+{\text{i}}\,y(0)=A+B\\{\dot {u}}(0)={\dot {x}}(0)+{\text{i}}\,{\dot {y}}(0)={\text{i}}\,\omega _{0}(A-B)\end{array}}}$

Simple special cases are:

• For there is a clockwise circular path (mathematically negative sense) with a radius . ${\displaystyle B=0}$ ${\displaystyle R=|A|}$
• For there is a counterclockwise circular path (mathematically positive sense) with a radius . ${\displaystyle A=0}$ ${\displaystyle R=|B|}$
• For there is a straight line between from point to point (and back). ${\displaystyle A=B\,(\neq 0)}$ ${\displaystyle {\begin{pmatrix}2\,{\text{Re}}(A)\\2\,{\text{Im}}(A)\end{pmatrix}}}$ ${\displaystyle {\begin{pmatrix}-2\,{\text{Re}}(A)\\-2\,{\text{Im}}(A)\end{pmatrix}}}$
• The result is the same straight line, but starting in the rest position. ${\displaystyle A=-B\,(\neq 0)}$

The harmonic oscillator outside of mechanics

Electrical oscillating circuit

Circuit diagram of an electrical oscillating circuit

→ Main article : resonant circuit

The electrical oscillating circuit is a harmonic oscillator in electrodynamics . While in mechanics potential and kinetic energy are periodically converted into one another, in the resonant circuit the electrical energy stored in a capacitor with the capacitance and the magnetic energy stored in a coil with the inductance are exchanged for each other. A differential equation results for the current strength : ${\displaystyle C}$ ${\displaystyle L}$ ${\displaystyle i}$

${\displaystyle {\ddot {i}}(t)+{\frac {1}{LC}}\,i(t)=0}$

The similarity with the equation of motion of the mechanical oscillator is obvious. The following table is intended to make the analogies between the mechanical and electrical oscillator clear:

mechanical (translation)	mechanical (torsion / rotation)	RLC series resonant circuit	RLC parallel resonant circuit
Deflection ${\displaystyle x}$	angle ${\displaystyle \varphi }$	charge ${\displaystyle q}$	tension ${\displaystyle u}$
speed ${\displaystyle {\dot {x}}\equiv v}$	Angular velocity ${\displaystyle {\dot {\varphi }}\equiv \omega }$	Amperage ${\displaystyle {\dot {q}}\equiv i}$	Rate of change of voltage ${\displaystyle {\dot {u}}}$
Dimensions ${\displaystyle m}$	Moment of inertia ${\displaystyle I}$	Inductance ${\displaystyle L}$	capacity ${\displaystyle C}$
Spring constant ${\displaystyle k}$	Torsion constant ${\displaystyle \mu }$	Reciprocal capacity ${\displaystyle 1/C}$	Reciprocal inductance ${\displaystyle 1/L}$
Damping constant ${\displaystyle d}$	Damping constant ${\displaystyle \Gamma }$	resistance ${\displaystyle R}$	Conductance ${\displaystyle 1/R}$
external force ${\displaystyle F(t)}$	external torque ${\displaystyle M(t)}$	external voltage ${\displaystyle u_{e}(t)}$	Rate of change in external current ${\displaystyle {\dot {i}}_{e}(t)}$
Undamped natural frequency : ${\displaystyle f_{0}}$
${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {\mu }{I}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$
Differential equation
${\displaystyle m{\ddot {x}}+d{\dot {x}}+kx=F(t)}$	${\displaystyle I{\ddot {\varphi }}+\Gamma {\dot {\varphi }}+\mu \varphi =M(t)}$	${\displaystyle L{\ddot {q}}+R{\dot {q}}+q/C=u_{e}(t)}$	${\displaystyle C{\ddot {u}}+{\dot {u}}/R+u/L={\dot {i}}_{e}(t)}$

The harmonic oscillator of quantum mechanics

→ Main article : harmonic oscillator of quantum mechanics

Since any potential can be developed around a stable equilibrium position and is then parabolic in the first approximation, the harmonic oscillator is a standard model in quantum mechanics. It is one of the few systems that an analytical solution is known for.

In quantum mechanics , the position, momentum and energy variables of a particle are replaced by operators . The Hamilton operator for the energy of a harmonic oscillator is given by

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+m\omega ^{2}{\frac {{\hat {x}}^{2}}{2}}}$.

The wave functions with which the probabilities of the particle's location can be calculated are eigenfunctions of the Hamilton operator. The energy levels correspond to the eigenvalues.

Lorentz oscillator in optics

The Lorentz oscillator is used in optics as a model to describe the behavior of the atoms of a solid under the influence of an electromagnetic wave. For example, the susceptibility , which counteracts the build-up of the field, is the analogue of damping through friction in mechanics. With the help of the Lorentz oscillator, optical phenomena such as birefringence or the complex refractive index can be explained in the Drude model.

Excitation of harmonic oscillators

See also : resonance

When energy is added to an oscillator, it is called stimulation. For the mechanical oscillator this means that either an external force acts or parameters of the oscillator such as the natural frequency change. The excitation of quantum mechanical oscillators is represented using ladder operators (see harmonic oscillator (quantum mechanics) ). The dissipation of energy, also called de-excitation, takes place in the same way. ${\displaystyle F_{\mathrm {ext} }}$ ${\displaystyle \omega _{0}}$

Forced vibration

→ Main article : Forced vibration

A forced oscillation is excited by an independent, usually periodic force or electrical voltage. An example of this is a dipole antenna . The differential equation, here the example of the damped oscillator, becomes inhomogeneous:

${\displaystyle {\ddot {x}}(t)+2\gamma {\dot {x}}(t)+\omega _{0}^{2}x(t)={\frac {F_{\mathrm {ext} }(t)}{m}}}$

Self-excited vibration

→ Main article : Self-excited vibration

One speaks of self-excited oscillation when the energy supply is controlled by a suitable control element and the oscillation process itself. Mathematically, such an energy supply can be realized, for example, by a special damping term in which the damping can become negative. Such a system is mostly non-linear. An example of this is the van der Pol oscillator .

Parameter-excited oscillation

→ Main article : Parametric oscillator

If the natural frequency of a harmonic oscillator changes over time due to a change in parameters such as the length of a pendulum , this is called a parameter-excited oscillation. An example is a swing with small deflections. ${\displaystyle \omega _{0}}$

Coupled harmonic oscillators

With two pendulums attached to a string, the energy of the oscillation is periodically transferred between the two pendulums.

A multi-dimensional harmonic oscillator in which the individual components, i.e. the harmonic oscillators along the main axes of the potential, are not independent but interact with one another, is called coupled. This means that the energy of the oscillation of the individual components no longer has to be retained, as it can be transferred from one component to another through the interaction.

Coupled mechanical oscillators are also called coupled pendulums . A mechanical interaction between two pendulums is created, for example, by connecting the masses of two separate pendulums with a spring. If several identical pendulums, arranged in a row, are each connected to their immediate neighbors via springs, the arrangement is called an oscillating chain. An interesting example in which the energy alternates between translational motion and rotational motion is the Wilberforce pendulum .

With the help of coupled oscillators, lattice vibrations can also be modeled in crystals , for example . Here the electrical interaction between the ions, molecules or atoms of the crystal lattice ensures the necessary coupling. The quantum mechanical consideration in the article Harmonic Oscillator (Quantum Mechanics) then leads to the phonons .

Continuum transition

See also : wave

Vibrations of a continuum , for example a string vibration, can be described with the aid of an infinitely dimensional coupled harmonic oscillator or an infinite number of one-dimensional coupled harmonic oscillators. The transition to an infinite number of oscillators is then carried out for a longitudinal wave. The method can also be carried out analogously for transverse waves .

Scheme of a spring oscillator with n coupled oscillators

We take the example of coupled oscillators of the mass , which are connected by springs with spring constants . We denote the deflection of the i th oscillator with . The distance between the individual masses is . The Lagrange function of this system is then: ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle k}$ ${\displaystyle q_{i}}$ ${\displaystyle l}$

${\displaystyle {\mathcal {L}}={\frac {m}{2}}\sum _{i=1}^{n}{\dot {q}}_{i}^{2}-{\frac {k}{2}}\sum _{i=0}^{n}(q_{i+1}-q_{i})^{2}}$

The equation of motion of the system can be derived from this as:

${\displaystyle m{\ddot {q}}_{i}=k((q_{i+1}-q_{i})-(q_{i}-q_{i-1}))}$

We divide this equation and get: ${\displaystyle kl^{2}}$

${\displaystyle {\frac {m}{k\,l^{2}}}{\ddot {q}}_{i}={\frac {1}{l}}\left({\frac {q_{i+1}-q_{i}}{l}}-{\frac {q_{i}-q_{i-1}}{l}}\right)}$

A continuum transition replaces the discrete index with a continuous coordinate and the discrete function with the wave function . For such a continuum limit is the same limit , , and taken so doing the following variables are held constant: ${\displaystyle i}$ ${\displaystyle x=i\cdot l}$ ${\displaystyle q_{i}(t)}$ ${\displaystyle \Psi (x,t)}$ ${\displaystyle n\to \infty }$ ${\displaystyle l\to 0}$ ${\displaystyle m\to 0}$ ${\displaystyle k\to \infty }$

• The total length ${\displaystyle (n+1)l}$
• The total mass and thus also the density ${\displaystyle nm}$ ${\displaystyle m/l}$
• The product of the spring constant and the spring length ${\displaystyle kl}$

The factor on the left of the equation is constant. Therefore this page can be written as ${\displaystyle {\frac {m}{k\,l^{2}}}}$

${\displaystyle {\frac {1}{c^{2}}}{\frac {\partial ^{2}\Psi }{\partial t^{2}}}}$

The right side of the equation can be rewritten as:

${\displaystyle \lim _{l\to 0}{\frac {1}{l}}\left({\frac {\Psi (x+l,t)-\Psi (x,t)}{l}}-{\frac {\Psi (x,t)-\Psi (x-l,t)}{l}}\right)}$

This is precisely the difference quotient for the second derivative . Namely, one obtains um with the help of a Taylor expansion ${\displaystyle x}$

${\displaystyle \lim _{l\to 0}\left({\frac {\Psi (x+l,t)-2\Psi (x,t)+\Psi (x-l,t)}{l^{2}}}\right)=\lim _{l\to 0}{\frac {1}{l^{2}}}\left({\frac {\partial ^{2}\Psi }{\partial x^{2}}}(x,t)\cdot l^{2}+{\mathcal {O}}(l^{4})\right)={\frac {\partial ^{2}\Psi }{\partial x^{2}}}(x,t)}$

The wave equation is thus obtained

${\displaystyle \left({\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-{\frac {\partial ^{2}}{\partial x^{2}}}\right)\Psi =0}$

Web links

Commons : Harmonic Oscillator  - collection of images, videos and audio files

• Harmonic oscillator, quantum mechanical
• ChemgaPedia on harmonic / anharmonic oscillator
• Detailed derivation of the solution for the damped harmonic oscillator .

Individual evidence

1. ↑ Wolfgang Demtröder: Experimentalphysik 1 . 4th edition. Springer, Berlin / Heidelberg 2006, ISBN 3-540-26034-X , p. 335-357 .
2. ↑ Wolfgang Nolting: Theoretical Physics 2 . 7th edition. Springer, Berlin / Heidelberg 2006, ISBN 3-540-30660-9 , pp. 103-104 .

Remarks

1. ↑ Time information refers to the graphic above; the distance between two points in time is a quarter of a period, so . ${\displaystyle {\frac {\pi }{2}}{\sqrt {m/k}}}$