String vibration

String oscillation, fundamental oscillation and overtones

The string oscillation is used to generate sound in string instruments such as violin , guitar or piano . After being stimulated by bowing , plucking or striking , the string performs a damped harmonic oscillation , with a standing transverse wave being formed.

Physical basics

Basics

Physically, a string is an essentially cylindrically shaped element that is very thin in comparison to its length and therefore pliable. The string is held at both ends and tensioned by opposing tensile forces - called tensioning force here. The oscillation of a string is essentially characterized by its radial deflection against the restoring force resulting from the axially acting tension force and the elasticity of the string, and its flywheel mass. The brackets can be rigid or flexible, and the clamping force can be varied. Strings of musical instruments generate sounds by entrainment of the surrounding air, the brackets or acoustic effects on microphones or (ferro) electromagnetic effects on suitable pickups. Supporting a string can serve to dissipate vibration. Picking up a string can be used to shorten the length (s) of oscillation and to stretch the string. A string is excited by bowing, flowing around it with a fluid, plucking, hitting or tapping on a fret / bridge. Strings that resonate are stimulated by the vibration of the air and the instrument.

Vibrators, which are rather short and stiff, may be cylindrical or board-shaped and swing out of their bending elasticity out to be a bending vibrator and distinguish themselves by the strings from. Bending elasticity is only a marginal phenomenon on strings: near the places where the strings are held, supported or tapped or where they are bowed; temporarily also when striking or plucking and letting go.

Consider the vibration

The propagation speed  ( m / s ) of the wave traveling back and forth along the length of the string (not to be confused with the speed  with which the string oscillates transversely at one point) is determined ${\displaystyle c}$ ${\displaystyle v}$

• Clamping force  ( N = kg m / s ² ) (Greek letter Psi ) ${\displaystyle \Psi }$
• String diameter  (m) and ${\displaystyle D}$
• Material density (kg / cubic meter) (rho) ${\displaystyle \rho }$

to:

(F. 1) . ${\displaystyle c={\frac {2}{D}}{\sqrt {\frac {\Psi }{\pi \rho }}}}$

This formula (F. 1) can be simplified by introducing the - area-related -

• Tensile stress ( Pa = kg m ⁻¹ s ⁻² ) (sigma) ${\displaystyle \sigma }$

This is calculated from the clamping force per circular ${\displaystyle \Psi }$

• String cross-sectional area (m²) ${\displaystyle A}$ ${\displaystyle =r^{2}\cdot \pi =(D/2)^{2}\cdot \pi }$

${\displaystyle \sigma =\Psi /((D/2)^{2}\cdot \pi )}$

Conversely, it follows for the clamping force:

${\displaystyle \Psi =\sigma \cdot ((D/2)^{2}\cdot \pi )}$

Substituting for in formula (F. 1) shortens the simple form ${\displaystyle \Psi }$

(F. 1A) . ${\displaystyle c={\sqrt {\frac {\sigma }{\rho }}}}$

The speed of propagation of  a wave is related to ${\displaystyle c}$

• Wavelength  (lambda) ${\displaystyle \lambda }$
• Oscillation period  (tau) or ${\displaystyle \tau }$
• Frequency   : ${\displaystyle f}$

${\displaystyle c={\frac {\lambda }{\tau }}=\lambda f}$

The length of the string  creates a fundamental oscillation in which the - only two - oscillation nodes are at the ends of the string, the wavelength is therefore twice the length of the string ( ). The following applies to the frequency  : ${\displaystyle L}$ ${\displaystyle \lambda =2L}$ ${\displaystyle f}$

${\displaystyle f={\frac {c}{2L}}={\frac {1}{DL}}{\sqrt {\frac {\Psi }{\pi \rho }}}}$

If you take the mass layer (kg per m) as a basis instead of the material density, you get for ${\displaystyle \mu }$ ${\displaystyle f:}$

${\displaystyle f={\frac {1}{L}}{\sqrt {\frac {\Psi }{4\mu }}}}$

This results in the following dependencies, which are also used in practice in musical instruments when tuning or playing:

• the shorter the (vibrating) string length  , the higher the frequency (half the length results in double the frequency). ${\displaystyle L}$
• the higher the clamping force  , the higher the frequency (four times the force results in double the frequency). ${\displaystyle \Psi }$
• the thinner the string, the higher the frequency (half the diameter  results in double the frequency). ${\displaystyle D}$

It can be seen that the mass coating only goes into the root, that is, you have to spin a string up to four times its mass per length in order to halve its resonance frequency. Therefore, high-density metals (copper, silver) are used to achieve low notes with short, not too thick strings.

Strings have an amplitude-dependent resonance frequency, as the average tension increases with larger amplitudes. This effect occurs especially with low tension and leads to the fact that the lower strings of an instrument sound higher when they are strongly bowed or plucked.

The oscillation equation

Illustration to derive the wave equation of the undamped, transverse string oscillation

A real string vibrates with an almost infinite number of “harmonic harmonics”, which are shown in the picture up to the seventh harmonic. Their frequencies are integral multiples of the frequency of the fundamental oscillation.
The amplitudes of the harmonics, i.e. their oscillation ranges, determine the sound, the so-called timbre of the oscillation. The distribution of the amplitudes over the harmonics is called the frequency spectrum of the sound.

Pythagoras is credited with being the first to recognize that tones differ by an octave when the length of the string is doubled or halved (with the same tension ), and that other intervals are also reflected in proportions of the string length. As a result, he used the length of the string as a measure of the pitch. Today it is not the string length but the frequency that is used as a measure of the pitch. The frequency is inversely proportional to the length of the string and the octave is twice as high a frequency. The development of calculus by Isaac Newton and Gottfried Wilhelm Leibniz enabled a more comprehensive theoretical description of a vibrating string. From Marin Mersenne and Joseph Sauveur the first explanations come to. Brook Taylor was the first to arrive at a representation of the fundamental oscillation, although the current methods for setting up and solving partial differential equations were not yet available to him. Building on Taylor's work in part, Johann I Bernoulli , Jean-Baptiste le Rond d'Alembert , and Leonhard Euler continued to work on the problem. By recognizing the existence of harmonics, Daniel Bernoulli arrives at a complete solution to the problem. Mersenne had already described two harmonics, but the idea was not pursued any further. ${\displaystyle \Psi }$

Daniel Bernoulli describes observations and experiments with various musical instruments, trumpets, flutes and stringed instruments, and concludes from this: “... that all vibrating bodies emit a multitude of tones ... In fact, all musicians agree that a plucked string is apart from its fundamental at the same time also emits other, much lighter tones ... This is the obvious proof that in one and the same string a superposition of several kinds of Taylor vibrations can occur at the same time ”. Daniel Bernoulli's “completely new idea, which not only clarifies the problem of the vibrating string, but also revolutionizes the whole of mathematical physics, was the construction of the general solution by superposing individual solutions”.

Euler considered Bernoulli's solution to be incomplete, as he did not believe that every initial situation (the way in which the string was plucked) could develop into an oscillation that could be represented by the sum of suitable sine functions. In fact, the proof of this was only possible through the work of Joseph Fourier ( Fourier analysis ) on the theory of heat.

One of Brook Taylor's basic ideas was the (correct) assumption that the curvature (kappa) at a point on the string is proportional to the acceleration of this point at any point : ${\displaystyle \kappa }$ ${\displaystyle x}$

${\displaystyle \kappa =c\cdot {\ddot {y}}(x,t).}$

It is the function that describes the position of the string at the place and time and ${\displaystyle y(x,t)}$ ${\displaystyle x}$ ${\displaystyle t}$

${\displaystyle {\ddot {y}}(x,t)={\frac {\partial ^{2}y(x,t)}{\partial t^{2}}}}$

its second partial derivative with respect to time (the acceleration at the position at the time , is a yet undetermined proportionality factor). The curvature is given by ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle c}$
${\displaystyle \kappa }$

${\displaystyle \kappa ={\frac {y''}{\sqrt {1+y'^{2}}}}}$

Here and are the first and the second partial derivative of to . If the string is deflected only a little out of its rest position, a good approximation can be made and the above proportionality equation becomes: ${\displaystyle y'(x,t)={\frac {\partial y(x,t)}{\partial x}}}$ ${\displaystyle y''(x,t)={\frac {\partial ^{2}y(x,t)}{\partial x^{2}}}}$ ${\displaystyle y(x,t)}$ ${\displaystyle x}$
${\displaystyle y'=0}$ ${\displaystyle \kappa =y''.}$ ${\displaystyle \kappa =c\cdot {\ddot {y}}(x,t)}$

${\displaystyle y''(x,t)=c\cdot {\ddot {y}}(x,t),}$

or, in more detail

${\displaystyle {\frac {\partial ^{2}y(x,t)}{\partial x^{2}}}=c\cdot {\frac {\partial ^{2}y(x,t)}{\partial t^{2}}}.}$

This is the partial differential equation of the vibrating string, known as the D'Alembert or homogeneous wave equation . The equation describes undamped vibrations, i.e. H. that it does not take into account the fading of a vibration, i.e. the sound becoming quieter.

The solution

${\displaystyle y(x,t)=A\cdot \sin(\alpha (x+x_{0}))\cdot \sin(\beta (t+t_{0})).}$		(Eq. 1)

is known from the theory of partial differential equations. The unknown quantities are still to be determined in this. ${\displaystyle A,\alpha ,x_{0},\beta {\text{ und }}t_{0}}$

Determination of and ${\displaystyle \alpha }$ ${\displaystyle x_{0}}$

We designate the length of the freely vibrating string with The string is clamped at and at , there is the deflection for each time ${\displaystyle L.}$ ${\displaystyle x=0}$ ${\displaystyle x=L}$ ${\displaystyle t}$ ${\displaystyle y=0:}$

${\displaystyle y(0,t)=A\cdot \sin \alpha (0+x_{0})\cdot \sin \beta (t+t_{0})=0.}$

Because it is not constant zero and would be nonsensical (it would represent the dormant string) is ${\displaystyle \sin \beta (t+t_{0})}$ ${\displaystyle A=0}$

${\displaystyle \sin \alpha (0+x_{0})=\sin \alpha x_{0}=0.}$

${\displaystyle \alpha =0}$would be just as nonsensical as , so from Eq. 1 will be ${\displaystyle A=0}$ ${\displaystyle x_{0}=0.}$

${\displaystyle y(x,t)=A\cdot \sin \alpha x\cdot \sin \beta (t+t_{0}).}$		(Eq. 2)

What applies to also applies to : ${\displaystyle x=0}$ ${\displaystyle x=L}$

${\displaystyle y(L,t)=A\cdot \sin \alpha L\cdot \sin \beta (t+t_{0})=0.}$

So is and (with arbitrary ), consequently Eq 2. becomes ${\displaystyle \sin \alpha L=0}$ ${\displaystyle \alpha L=n\cdot \pi }$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle \textstyle \alpha ={\frac {n\pi }{L}}.}$

${\displaystyle y_{n}(x,t)=A_{n}\cdot \sin {\frac {n\pi }{L}}x\cdot \sin \beta (t+t_{0}).}$		(Eq. 3)

If the string is in its rest position at the time, we get analogously and from Eq. 3 will ${\displaystyle t=0}$ ${\displaystyle t_{0}=0}$

${\displaystyle y_{n}(x,t)=A_{n}\cdot \sin {\frac {n\pi }{L}}x\cdot \sin \beta t.}$		(Eq. 4)

${\displaystyle \beta }$is obviously a circular frequency , we set with an as yet indefinite oscillation period. So we get ${\displaystyle \beta ={\frac {2n\pi }{\tau }}}$ ${\displaystyle \tau .}$

${\displaystyle y_{n}(x,t)=A_{n}\cdot \sin {\frac {n\pi }{L}}x\cdot \sin {\frac {2n\pi }{\tau }}t.}$		(Eq. 5)

The , for each of a solution of the Eq. 1, i.e. also the sum of all D. h. that ${\displaystyle y_{n}(x,t)}$ ${\displaystyle n}$ ${\displaystyle y_{n}(x,t).}$

${\displaystyle y(x,t)=A_{1}\cdot \sin {\frac {\pi }{L}}x\cdot \sin {\frac {2\pi }{\tau }}t+A_{2}\cdot \sin {\frac {2\pi }{L}}x\cdot \sin {\frac {4\pi }{\tau }}t+A_{3}\cdot \sin {\frac {3\pi }{L}}x\cdot \sin {\frac {6\pi }{\tau }}t+\ldots }$		(Eq. 6)

the complete solution of Eq. 1 with as yet undetermined . The are the amplitudes of the harmonics. You hang z. B. the material of the string (steel, gut, plastic), wound or not, the tension of the string, the type of tearing of the side (thumb or pick), the location of the tearing (in the middle or above the sound hole) and on the shape, size and material of the sound body. In addition, the sound subsides, i.e. H. that the amplitudes become smaller. The individual amplitudes are generally attenuated to different degrees, so they do not all decay in the same way, the tone can sound different immediately after it is picked than it does later. ${\displaystyle \tau }$ ${\displaystyle A_{n}}$ ${\displaystyle A_{n}}$

Determination of ${\displaystyle \tau }$

The statement about the frequency of the oscillation or its period of oscillation is obtained through the relationship between the frequency , the wavelength and the speed of propagation of a wave: ${\displaystyle f}$ ${\displaystyle \textstyle \tau ={\frac {1}{f}}}$ ${\displaystyle f}$ ${\displaystyle \lambda }$ ${\displaystyle c}$

${\displaystyle \lambda ={\frac {c}{f}}.}$

From the theory of elasticity we know the speed of propagation of a wave in a tensioned string (see above):

${\displaystyle c={2 \over D}{\sqrt {\Psi \over \pi \rho }}.}$

For the fundamental

${\displaystyle y_{1}(x,t)=A_{1}\cdot \sin {\frac {\pi }{L}}x\cdot \sin {\frac {2\pi }{\tau }}t}$ is

we get the wavelength Mit from : ${\displaystyle \lambda =2L.}$ ${\displaystyle f={\frac {1}{\tau }}}$ ${\displaystyle \lambda ={\frac {c}{f}}}$

${\displaystyle 2L={\frac {1}{f}}\cdot {2 \over D}{\sqrt {\Psi \over \pi \rho }}=\tau \cdot {2 \over D}{\sqrt {\Psi \over \pi \rho }},}$

so

${\displaystyle f={\frac {1}{LD}}{\sqrt {\frac {\Psi }{\pi \rho }}}}$

or

${\displaystyle \tau =LD{\sqrt {\pi \rho \over \Psi }}.}$

As a reminder: is the frequency of the fundamental oscillation , is its period of oscillation, the length of the string, its diameter, its density, i.e. mass per volume, and the tension of the string. The frequencies of the harmonics are integer multiples of the frequency of the fundamental. ${\displaystyle f}$ ${\displaystyle \tau }$ ${\displaystyle L}$ ${\displaystyle D}$ ${\displaystyle \rho }$ ${\displaystyle \Psi }$

Mathematical description of the plucked string

Undamped vibration

The following is a is the beginning - boundary value -problem (ARWP) of the D'Alembert equation presented as a model of undamped string vibration. The local boundary values ​​(RWP) are set to zero, which corresponds to a string clamped at the ends. The initial value problem (AWP) is designed so that at the point in time the string has a deflection that corresponds to the periodic function . Furthermore, the speed of the string is set to zero at the time, which means that the string is at rest. Bending moments are neglected in this model. If bending moments are taken into account, there is also a partial derivative of the fourth order according to the location coordinate . ${\displaystyle t=0{\text{s}}}$ ${\displaystyle g(x)}$ ${\displaystyle {\frac {\partial u}{\partial t}}}$ ${\displaystyle t=0{\text{s}}}$ ${\displaystyle x}$

${\displaystyle {\frac {\partial ^{2}u(x,t)}{\partial x^{2}}}={\frac {1}{c_{0}^{2}}}\cdot {\frac {\partial ^{2}u(x,t)}{\partial t^{2}}}\quad {\text{mit}}\quad u(0,t)=u(L,t)=0\;{\text{(RWP)}}\quad {\text{und}}\quad u(x,0)=g(x)\;\wedge \;{\frac {\partial u}{\partial t}}(x,0)=0\;{\text{(AWP)}}}$

Definition of parameters:

• Wave function: ${\displaystyle u(x,t)}$
• String length in m: ${\displaystyle L\in \mathbb {R} \quad \wedge \quad L>0}$
• Picking position in m: ${\displaystyle l\in \mathbb {R} \quad \wedge \quad 0\leq l\leq L}$
• Standardized picking position: ${\displaystyle b=l/L\quad \rightarrow \quad 0\leq b\leq 1}$
• Clamping force in N: ${\displaystyle \Psi \in \mathbb {R} \quad \wedge \quad \Psi >0}$
• Material density in kg / m ^ 3: ${\displaystyle \rho \in \mathbb {R} \quad \wedge \quad \rho >0}$
• String thickness in m: ${\displaystyle D\in \mathbb {R} \quad \wedge \quad D>0}$
• nth angular frequency of the undamped oscillation in 1 / s: ${\displaystyle \omega _{0n}=k_{n}\cdot c_{0}}$
• nth wave propagation constant in 1 / m: ${\displaystyle k_{n}=\pi n/L}$
• nth amplitude: ${\displaystyle A_{n}}$
• Speed ​​of propagation of the wave in m / s: ${\displaystyle c_{0}={\frac {2}{D}}{\sqrt {\frac {\Psi }{\pi \rho }}}}$

One possible solution to this initial-boundary value problem is the product of a sine and a cosine function. The sine function is suitable for describing the local oscillation, since it fulfills the boundary value problem (RWP). When checking the boundary value problem one obtains the formula for and the restriction of . The relationship between and results from inserting the solution approach into d'Alembert's wave equation. ${\displaystyle u_{n}(x,t)}$ ${\displaystyle k_{n}}$ ${\displaystyle n}$ ${\displaystyle k_{n}}$ ${\displaystyle \omega _{0n}}$ ${\displaystyle u_{n}(x,t)}$

${\displaystyle u_{n}(x,t)=A_{n}\cdot \sin(k_{n}x)\cdot \cos(\omega _{0n}t)\quad {\text{mit}}\quad k_{n}={\frac {\pi n}{L}}\;,\quad \omega _{0n}=k_{n}c_{0}\quad {\text{und}}\quad n\in \mathbb {N} \wedge n\geq 1}$

By defining , it is obvious that there are infinitely many solutions . Using a Fourier series, all of these solutions can be recorded in a formula. This Fourier series therefore corresponds to the sum that contains the fundamental and all harmonics. ${\displaystyle n}$ ${\displaystyle u_{n}(x,t)}$

${\displaystyle u(x,t)=\sum _{n=1}^{\infty }A_{n}\sin \left(k_{n}x\right)\cos \left(\omega _{0n}t\right)\quad {\text{und}}\quad A_{n}={\frac {2}{L}}\int _{0}^{L}g(x)\sin \left(k_{n}x\right)dx}$

Initial value problem of the plucked string g ( x ).

According to the theory of Fourier series, the amplitudes can be determined with an integral. This completely describes the initial value problem. For the idealized description of the plucked string, the function is a triangle function. This is shown in the figure "Initial value problem of the plucked string g (x)". Formally it is as follows. ${\displaystyle A_{n}}$ ${\displaystyle g(x)}$ ${\displaystyle g(x)}$

${\displaystyle g(x)=h_{0}\cdot {\begin{cases}{\frac {x}{bL}}&0\leq x\leq bL\\{\frac {L-x}{L-bL}}&bL\leq x\leq 2L-bL\\{\frac {x-2L}{bL}}&2L-bL\leq x\leq 2L\end{cases}}\quad {\text{mit}}\quad 0\leq b\leq 1}$

The associated Fourier coefficients and the wave function result from: ${\displaystyle A_{n}}$ ${\displaystyle u(x,t)}$

${\displaystyle A_{n}={\frac {1}{L}}\int _{0}^{2L}g(x)\sin \left(k_{n}x\right)\mathrm {d} x={\frac {2h_{0}\sin \left(\pi bn\right)}{\pi ^{2}n^{2}L(b-b^{2})}}={\frac {2h_{0}{\text{sin}}(\pi bn)}{k_{n}^{2}L^{3}(b-b^{2})}}}$

Animation of the vibration of the plucked string with b = 0.8; c = 1; h ₀ = 1; L = 1. This animation was calculated with 200 terms of the Fourier series.

${\displaystyle u(x,t)={\frac {2h_{0}}{L^{3}(b-b^{2})}}\sum _{n=1}^{\infty }\left[{\frac {\sin \left(\pi bn\right)\sin \left(k_{n}x\right)\cos \left(k_{n}c_{0}t\right)}{k_{n}^{2}}}\right]}$

An animation of this formula with an approximation of 200 sum terms is shown on the right. In order to be able to enter this formula in the computer it can be discretized as follows, where the number of points is in the x-direction and the step size in the x-direction. is the number of Fourier terms. ${\displaystyle M}$ ${\displaystyle \Delta x}$ ${\displaystyle N}$

${\displaystyle u_{m,n}(t)={\frac {1}{k_{n}^{2}}}\sin \left(\pi bn\right)\cdot \sin \left(k_{n}\cdot m\Delta x\right)\cdot \cos \left(\omega _{0n}t\right)}$

${\displaystyle {\text{mit}}\quad \Delta x={\frac {L}{M}}}$

${\displaystyle {\overrightarrow {U_{N}}}(t)={\frac {2h_{0}}{L^{3}(b-b^{2})}}\sum _{n=1}^{N}{\begin{pmatrix}u_{0,n}(t)\\\vdots \\u_{M,n}(t)\end{pmatrix}}}$

Damped vibration

In the case of damped oscillation, the partial differential equation contains an additional first-order derivative over time. In the following the oscillation equation can be seen as (ARWP):

${\displaystyle {\frac {\partial ^{2}u(x,t)}{\partial x^{2}}}={\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}u(x,t)}{\partial t^{2}}}+{\frac {2\alpha }{c_{0}^{2}}}{\frac {\partial u(x,t)}{\partial t}}}$

${\displaystyle {\text{mit}}\quad u(0,t)=u(L,t)=0\;{\text{(RWP)}}\quad {\text{und}}\quad u(x,0)=g(x);\quad u'(x,0)=0\;{\text{(AWP)}}\quad {\text{und}}\quad c_{0}={\frac {2}{D}}{\sqrt {\frac {\Psi }{\pi \rho }}}}$

The solution to this initial boundary value problem is similar to the solution of the undamped oscillation except for a decaying exponential function and a different angular frequency over time. For further completion, a time-dependent step function (Heaviside) (theta) can be multiplied, which fades out the negative time range of the oscillation. This describes that the string is struck at the time . ${\displaystyle \theta (t)}$ ${\displaystyle t=0}$

${\displaystyle u(x,t)=\mathrm {e} ^{-\alpha t}\theta (t)\sum _{n=1}^{\infty }A_{n}\sin \left(k_{n}x\right)\cos(\omega _{n}t)\quad {\text{mit}}\quad A_{n}={\frac {1}{L}}\int _{0}^{2L}g(x)\sin(k_{n}x)\mathrm {d} x;\quad k_{n}={\frac {\pi n}{L}};\quad \omega _{n}={\sqrt {\omega _{0n}^{2}-\alpha ^{2}}};\quad \omega _{0n}=k_{n}c_{0}}$

Animation of the damped string oscillation with L = 2; b = 0.8; c ₀ = 20; h ₀ = 0.1 and α = 0.3.

The Fourier coefficients in this case are exactly the same as for the undamped oscillation, since the deflection of the string is the same at the time . The function can thus be represented as follows: ${\displaystyle A_{n}}$ ${\displaystyle t=0}$

${\displaystyle u(x,t)=\mathrm {e} ^{-\alpha t}\theta (t)\sum _{n=1}^{\infty }{\frac {2h_{0}\sin \left(\pi bn\right)\sin \left(k_{n}x\right)\cos \left(\omega _{n}t\right)}{\pi ^{2}n^{2}bL(1-b)}}}$

An animation of this formula can be seen in the graphic opposite. 200 terms of the Fourier series were calculated and 200 points in the x-direction. The parameters used are given below. If you want to watch the animation, you should click on the graphic.

Intermodal dispersion

In contrast to undamped oscillation, in which all modes have the same propagation speed , the propagation speed differs depending on the waveform. Due to the different propagation speeds, there are equally differences in the transit time of the waves. As a result of this effect, the basic form of the excited oscillation becomes more and more blurred over time. The basic shape melts like ice in the sun. If the damping factor is relatively small, this effect is weaker than in the case of large damping. The following is the formula for the speed of propagation : ${\displaystyle c_{0}}$ ${\displaystyle \alpha }$ ${\displaystyle v_{n}}$

${\displaystyle v_{n}={\frac {\omega _{n}}{k_{n}}}={\sqrt {c_{0}^{2}-{\frac {\alpha ^{2}}{k_{n}^{2}}}}}\quad {\text{mit}}\quad c_{0}={\frac {2}{D}}{\sqrt {\frac {\Psi }{\pi \rho }}}\quad {\text{und}}\quad k_{n}={\frac {\pi n}{L}}}$

Spectral analysis (Fourier transform)

Suppose we install an ideal pickup at this point, which converts the vibration form of the string into an electrical signal at precisely this point . This signal could now be viewed with an oscilloscope in the time domain and in the frequency domain (spectral domain ). A decaying cosine oscillation would then be seen in the time domain and the fundamental oscillation contained in the signal and the harmonics in the spectral domain. In order to obtain the theoretical frequency spectrum, the Fourier transform has to be applied to the previously derived function . ${\displaystyle x_{1}=0{,}25L}$ ${\displaystyle u(x,t)}$

${\displaystyle U(x,\omega )=\int _{-\infty }^{\infty }u(x,t)\cdot e^{-j\omega t}\mathrm {d} t=\sum _{n=1}^{\infty }\left({\frac {2h_{0}\sin \left(\pi bn\right)\sin \left(k_{n}x\right)}{\pi ^{2}n^{2}bL(1-b)}}\cdot \int _{0}^{\infty }\cos \left(\omega _{n}t\right)\mathrm {e} ^{-(\alpha +j\omega )t}\mathrm {d} t\right)}$

For the integral vanishes due to the Heaviside function , which means that the lower integration limit is set to zero. The solution then looks like this: ${\displaystyle t<0}$

${\displaystyle U(x,\omega )=\sum _{n=1}^{\infty }\left({\frac {2h_{0}\sin \left(\pi bn\right)\sin \left(k_{n}x\right)}{\pi ^{2}n^{2}bL(1-b)}}\cdot {\frac {\alpha +j\omega }{(\alpha +j\omega )^{2}+\omega _{n}^{2}}}\right)}$

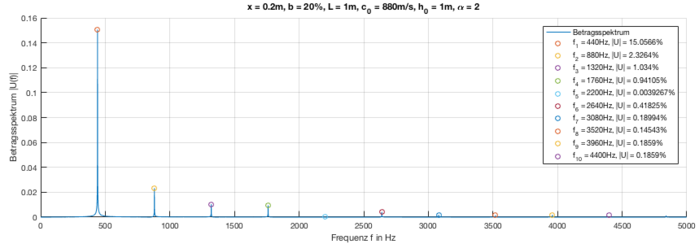
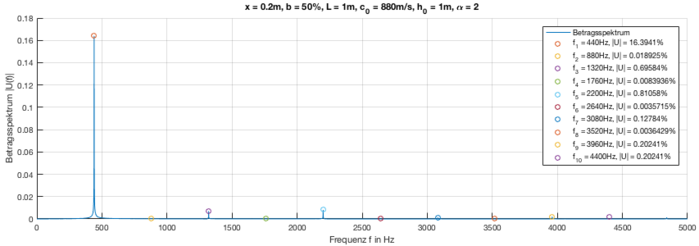
The following table contains audio examples with different attack positions and the corresponding amount spectrum. It should be noted that the timbre changes by varying the touch or pickup position. If you hit the end of the string, the tone sounds metallic. On the other hand, if you hit the middle part of the string, the tone sounds softer. If you compare this with a real musical instrument, you can hear the same behavior. If you look at the graphs of the magnitude spectra, the peaks pointing upwards are the overtones contained in the signal. This shows that the respective timbre is created by which overtones with which amplitudes are contained in the acoustic signal.

Plucking position b	Acoustic reproduction	Plot of the magnitude spectra
10%
20%
30%
40%
50%

literature

• István Szabó : History of Mechanical Principles . 3. Edition. Birkhäuser, Basel / Boston / Berlin 1987, ISBN 978-3-0348-9980-2 .

Individual evidence

1. ^ Susan Sales Harkins, William H. Harkins: The Life and Times of Pythagoras . Mitchell Lane Publishers, Inc., 2007, ISBN 1-61228-885-5 , pp. 29 ( limited preview in Google Book search).
2. ↑ William A. Sethares: tuning, Timbre, Spectrum, Scale . Springer Science & Business Media, 2013, ISBN 1-4471-4177-6 , pp. 33 ( limited preview in Google Book search).
3. ↑ Marin Mersenne: Harmonicorum libri . 1636.
4. ↑ Brook Taylor: Methodus Incrementorum Directa et Inversa . London 1717, available as a digital edition from the Hamburg State Library.
5. ^ Johann Bernoulli: Meditationes de cordis vibrantibus . Opera Omina, Tom. II.
6. ^ Jean-Baptiste le Rond d'Alembert: Recherches sur la courbe que forme une corde tendue mise en vibration . Histoire de l'academie Royale de science et belle lettre année, 1747.
7. ^ Leonhard Euler: Sur la vibration de cordes . Histoire de l'academie Royale de science et belle lettre année, 1748.
8. ^ Daniel Bernoulli: Reflexions et Eclaircissemens sur le nouvelles vibrations des cordes . Histoire de l'Académie de Berlin IX, 1753.
9. ^ Daniel Bernoulli, ibid, p. 181.
10. ↑ István Szabó : History of Mechanical Principles . 3. Edition. Birkhäuser, Basel / Boston / Berlin 1987, ISBN 978-3-0348-9980-2 , p. 339.
11. ↑ Brook Taylor, ibid, Lemma IX, p. 88.
12. ^ Zollner, Manfred .: Physics of the electric guitar. Self-rel. by the author, 2014 ( worldcat.org [accessed June 25, 2020]).