Phase velocity

The red point is always at the point of the same phase (wave crest) and moves with the phase velocity of the blue, monochromatic wave.

A wave packet propagates in a non-dispersive medium (e.g. an electromagnetic wave in a vacuum ).

A wave packet propagates in a dispersive medium.

The phase velocity is the speed of propagation of the same phases of a monochromatic wave .

In dispersive media , waves of different frequencies propagate with different phase velocities. With the propagation of wave packets (i.e. the sum of several superimposed monochromatic waves) in dispersive media, the phase differences between individual components are consequently not constant, but time-dependent: The shape of the wave pack changes (it "dissolves").

In the figure above, the red point moves with the phase velocity. The second figure shows a wave packet whose group velocity is equal to the phase velocities of the individual components. In the third figure, the phase velocities of the individual components are different.

The phase velocity is calculated from the wavelength (the distance that is covered) and the period (the time it takes) ${\displaystyle v_{\mathrm {p} }}$ ${\displaystyle \lambda \,}$ ${\displaystyle T\,}$

${\displaystyle v_{\mathrm {p} }={\frac {\lambda }{T}}.}$

The definition of frequency , angular frequency and angular wave number results in the equivalent representation ${\displaystyle f\,}$ ${\displaystyle \omega \,}$ ${\displaystyle k\,}$

${\displaystyle v_{\mathrm {p} }=\lambda \cdot f={\frac {\omega }{k}}.}$

The speed of light in a vacuum is the upper limit for the transmission speed of energy and information. However, there are numerous cases in which phase velocities above the speed of light occur. Examples are matter waves and waves in waveguides .

Relationship with group speed and dispersion

designation	symbol	Relationships
amplitude	${\displaystyle {\vec {A}}_{0}}$	${\displaystyle {\vec {A}}_{0}\perp {\vec {k}}}$ Transverse wave ${\displaystyle {\vec {A}}_{0}\|{\vec {k}}}$ Longitudinal wave
Wave vector	${\displaystyle {\vec {k}}}$	Direction of propagation
Circular wavenumber	${\displaystyle k\,}$	${\displaystyle k=|{\vec {k}}|}$
wavelength	${\displaystyle \mathbf {\lambda } }$	${\displaystyle \lambda ={\frac {2\pi }{k}}}$
Angular frequency	${\displaystyle \mathbf {\omega } }$	${\displaystyle \mathbf {\omega } {\big (}{\vec {k}}{\big )}}$ Dispersion relation
frequency	${\displaystyle f}$	${\displaystyle f={\frac {\omega }{2\pi }}}$
Phase velocity	${\displaystyle v_{\mathrm {p} }}$	${\displaystyle v_{\mathrm {p} }={\frac {\omega }{k}}=\lambda f}$
Group speed	${\displaystyle v_{\mathrm {g} }}$	${\displaystyle v_{\mathrm {g} }={\frac {\partial \omega }{\partial k}}}$
Phase angle	${\displaystyle \varphi }$	${\displaystyle \varphi ={\vec {k}}\cdot {\vec {r}}-\omega t}$

For the mathematical description of a wave in a special medium, one needs its wave form , amplitude , frequency , phase angle and the corresponding wave equation - possibly with boundary conditions . Nevertheless, different speeds can be assigned to such a clearly defined wave, which should not be confused with the phase speed.

The speed at which a wave transmits energy or information is the speed of the signal . For a lossless medium, this is equal to the group speed , i.e. the speed of a wave packet . Such a wave packet is composed of monochromatic waves with different frequencies . Each of these monochromatic waves has its own phase velocity: ${\displaystyle f}$

${\displaystyle v_{\mathrm {p} }=v_{\mathrm {p} }(f)}$.

The functional relationship between phase velocity and frequency is called dispersion .

For electromagnetic waves , the phase velocity and the group velocity in a vacuum are equal to the speed of light , i.e. H. the vacuum is not dispersive. In matter, however, the phase velocity is generally dependent on the frequency. Because of the relationship for the refractive index , the frequency dependence of the refractive index is referred to here as dispersion . ${\displaystyle v_{\mathrm {p} }}$ ${\displaystyle v_{\mathrm {g} }}$ ${\displaystyle c}$ ${\displaystyle n=c/v_{\mathrm {p} }}$ ${\displaystyle n(f)}$

Examples

Structure-borne noise

Lamb modes for two different materials with a Poisson's number (e.g. titanium ) and (e.g. steel )
${\displaystyle \sigma =0{,}34}$ ${\displaystyle \sigma =0{,}27}$

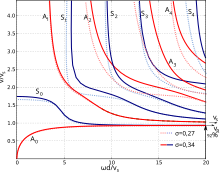
Sound waves can propagate as structure-borne sound in solids . The phase velocities are different depending on the wave type . For example, the phase velocity of the longitudinal wave at room temperature in stainless steel is about 5980 m / s; the phase velocity of the transverse wave is about a factor of 1.8 lower: approx. 3300 m / s. There are other types of waves in thin plates, so-called Lamb waves . In the picture opposite, each branch corresponds to a lamb wave type (mode). The phase velocity is shown vertically in units of the transverse wave velocity , horizontally the frequency as the product of the angular frequency and plate thickness in units of the transverse wave velocity . The higher modes only exist from certain minimum frequencies and then propagate at very high phase velocities. The mode has a vanishing phase velocity for small frequencies. ${\displaystyle v}$ ${\displaystyle v_{\mathrm {s} }}$ ${\displaystyle \omega }$ ${\displaystyle d}$ ${\displaystyle S_{1},A_{1},S_{2},A_{2},\dots }$ ${\displaystyle A_{0}}$

Matter wave

According to the wave-particle dualism , a particle, e.g. B. assign a wavelength and thus a phase velocity to an electron with the energy and the momentum ${\displaystyle E}$ ${\displaystyle p}$ ${\displaystyle \lambda }$

${\displaystyle v_{\mathrm {p} }=f\lambda ={\frac {\omega }{k}}={\frac {E}{p}}}$.

With Einstein's formula

${\displaystyle E=mc^{2}}$

or in the formulation with the Lorentz factor ${\displaystyle \gamma }$

${\displaystyle E=m_{0}\gamma c^{2}}$

and follows the definition of the relativistic impulse ${\displaystyle p=m_{0}\gamma v}$

${\displaystyle v_{\mathrm {p} }={\frac {m_{0}\gamma c^{2}}{m_{0}\gamma v_{\mathrm {g} }}}={\frac {c^{2}}{v_{\mathrm {g} }}}.}$

Here is the speed of light , the highest speed that energy or information can travel. The group speed is the particle speed , which is always less than . thats why ${\displaystyle c}$ ${\displaystyle v_{\mathrm {g} }={\frac {\mathrm {d} \omega }{\mathrm {d} k}}}$ ${\displaystyle c}$

${\displaystyle v_{\mathrm {p} }>c}$.

The de Broglie phase velocity is therefore always greater than the speed of light. This so-called superluminal speed of matter waves does not contradict the theory of relativity , since it is the signal speed . ${\displaystyle v_{\mathrm {g} }}$

Waveguide

Also electromagnetic waves in normal, used for power transmission waveguides move with phase velocities above the speed of light. In the traveling wave accelerator , the phase speed must be artificially reduced to values ​​below the speed of light by regularly arranged conductive screens.

literature

• DIN 1311, sheet 1: Vibrations and vibratory systems. Part 1: Basic concepts, classification. Edition 2000–2002.

Web links

• Java animation illustrating group speed and phase speed

Individual evidence

1. ^ Paul A. Tipler , Gene Mosca : Physics . For scientists and engineers. Ed .: Dietrich Pelte. 2nd Edition. Spectrum Academic Publishing House, 2007, ISBN 978-3-8274-1164-8 .
2. ^ Gunnar Lindström, Rudolf Langkau, Wolfgang Scobel: Physics compact 3: Quantum physics and statistical physics . Springer, 2013, ISBN 3-642-56017-2 , pp. 54 ( limited preview in Google Book search).
3. ↑ Wolfgang Demtröder : Experimentalphysik 3 . Atoms, molecules and solids. Springer DE, 2010, ISBN 978-3-642-03911-9 , pp. 97 ( limited preview in Google Book search).
4. ↑ Peter Schmüser: Theoretical Physics for Students of the Teaching Degree 1: Quantum Mechanics . Springer DE, 2012, ISBN 978-3-642-25395-9 , pp. 125 ( limited preview in Google Book Search).