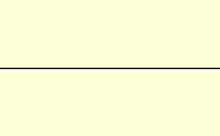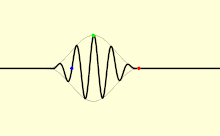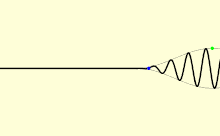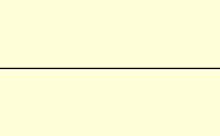Signal speed
The signal speed is the speed at which a signal propagates. A signal, i.e. a change in a state, can be described as a wave packet . The speed at which the envelope of such a wave packet moves is the group speed . In general, especially if the phase velocity is strongly frequency-dependent or the absorption cannot be neglected, the signal velocity must be distinguished from the group velocity. The speed at which the first deflection of a wave front moves is the front speed . This speed, and with it the signal speed, is always less than the speed of light . In cables it is indicated by the shortening factor.
Front speed
In the 19th century took Lord Rayleigh that a wave information, and transmits power with group velocity. In propagation media with anomalous dispersion , the group velocity is proportional to the amount of dispersion. There is no fundamental physical limit. It is possible that the center of a wave packet moves faster than light . According to the special theory of relativity , however, the speed of light is the highest speed at which information can be transmitted.
Using the telegraph equation , Woldemar Voigt showed that the speed of a wavefront in the case of this telegraph equation is less than the group speed, so that the signal speed must be distinguished from the group speed. The front of a wave is defined by a surface behind which the amplitude of a wave is identically zero at a certain point in time.
Faster than light
The fact that the front speed is always less than the speed of light can be seen from a general signal of the form
demonstrate. is here the Heaviside function . If the wave front of this wave cannot move faster than light, the wave function must be zero for a distance . For the wave function
with the greens function
this can be shown using the residual theorem . Since the refractive index is for high frequencies , there remains as an integrand. For we can write this as a line integral over the upper half of the complex plane. Since the refractive index is analytical there (i.e. it has no singularities) the integral is zero.
literature
- Léon Brillouin: "Wave propagation and group velocity" , Academic Press Inc., New York, 1960
Web links
- gregegan.customer.netspace.net.au - applet that shows the group, phase and signal speed of a wave.
- For the history of terms in Sommerfeld, Brillouin, Duke University
Individual evidence
- ↑ a b P.W. Milonni: Fast Light, Slow Light and Left-Handed Light . CRC Press, 2004, ISBN 1-4200-3433-2 , pp. 26 ( limited preview in Google Book search).
- ^ Léon Brillouin: Wave Propagation and Group Velocity . Academic Press, 2013, ISBN 1-4832-7601-5 , pp. 10 ( limited preview in Google Book search).