Enveloping
In mathematics , envelope (also called envelope curve or envelope , from French enveloppe , envelope ' ) describes a curve that envelops a family of curves . This means that the envelope touches each coulter curve once. Envelopes arise, among other things, with moving objects, e.g. B. when opening and closing a garage door. Every plane curve is the envelope curve of its tangents.
The evolution E of a plane curve C is the envelope curve of its normal . C is then the involute of E .
definition
A curve is an envelope of a family of curves if the following conditions are met:
- The curve is touched by one of the curves at each of its points .
- The curve touches every element of the family of curves at a point x h .
Calculation of envelope functions
- The function f ( x , t ) is derived with respect to t and the zeros t 0 are determined as a function of x of this derivation.
- In f ( x , t ) we substitute t 0 for t and get a candidate h ( x ) for the envelope function.
- Find all x h for which H touches an element of K t .
- It is shown that all elements of K t touch the curve H at at least one point.
Examples
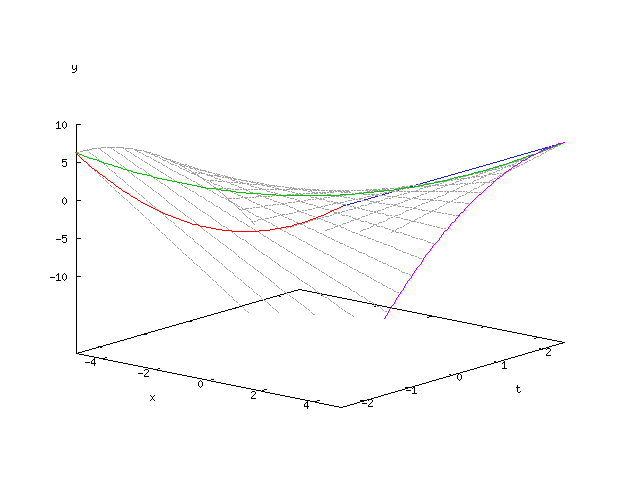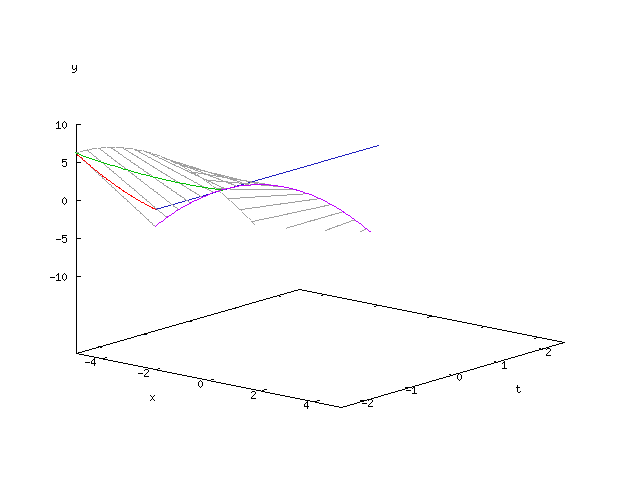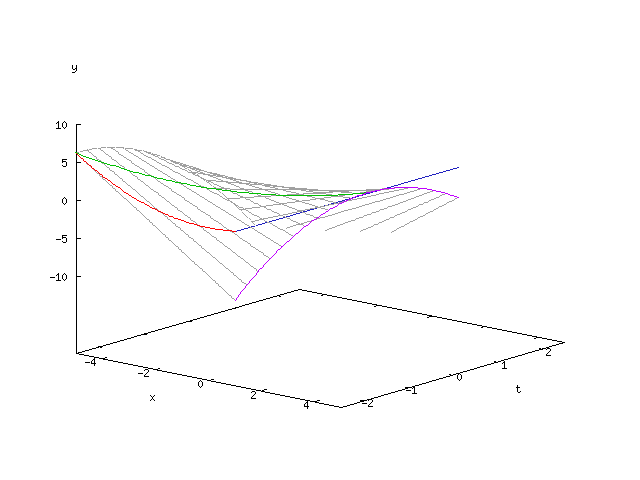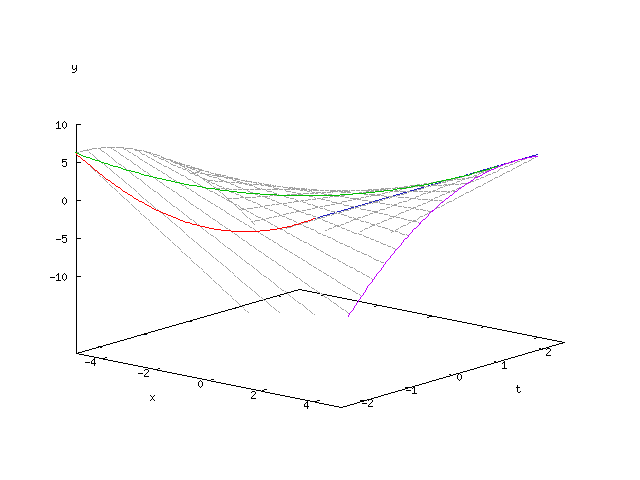
Three-dimensional envelope
Given is the equation parameterized by and the
defined family of lines.
As shown above, the envelope of this family of lines is given by the equations
given. Elimination of provides the parameter-free representation of the envelope:
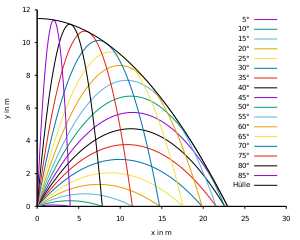
Trajectory parabolas
Another example is the envelope of trajectory parabolas. Details are given under Enveloping trajectory parabola .
application
Envelopes are a good way to describe the space required for moving objects. So you can use envelope curves to determine whether you will get a cupboard around a corner in the hallway, or how narrow a street can be in a curve, and how it has to look so that a truck can drive safely on it. For most technical applications, numerical methods are best.
In economics, cost functions that change over time are also referred to as upper and lower envelopes. I.e. between these two lies the entire spectrum of the cost curve, or in other words: at any given point in time, the true cost function is realized within the upper and lower envelope.
Envelopes of surfaces
Surfaces can also be described as envelopes of families of surfaces. z. B .:
- Channel and pipe surfaces are the envelopes of spherical shares.
- Slope surfaces are the envelopes of cone families.
literature
- Richard Courant, Fritz John: Introduction to Calculus and Analysis II / 1 . Reprint of the 1989 Edition, Springer-Verlag Berlin, 1991, ISBN 3-540-66569-2 .
- Michael Spivak: A Comprehensive Introduction to Differential Geometry . Vol. 3. 2. ed. Publish or Perish, Houston TX 1979, ISBN 0-914098-82-9 .
- WI Smirnow: Course of higher mathematics , part II. German publishing house of the sciences, Berlin 1990, ISBN 3-326-00029-4 .
Individual evidence
- ↑ mathematik.bildung-rp.de (PDF) or as a caustic in a coffee cup.
- ↑ jan.orend.lg-bs.de ( Memento of the original from January 8, 2006 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.