Slope area
If you pour earth along the edge of the road , which rises above a ground level, a slope body is created , the surface of which is called the slope surface .
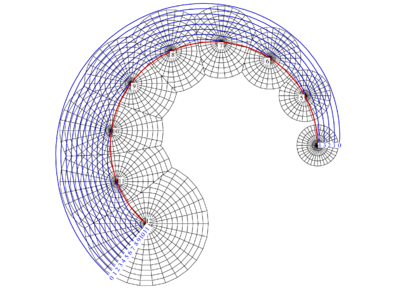
Mathematically, one can imagine an embankment surface as the envelope of a family of cones (the pouring cones ), the tips of which are located on a given curve (roadside) (see FIG. 1). The surface of the slope touches each cone in a straight line . Such straight lines are called fall lines . In order to draw a quoted projection of a slope area, one must determine contour lines . Since each contour line touches every cone in a height circle, one can imagine a contour line as the envelope of a family of (height) circles of cones (see FIG. 2). This is the key to drawing contour lines of the slope area in the associated listed projection (see Figure 3).
In practice (see Figure 4) the curve (roadside) is listed and the material- dependent steepness of the cone of material determines the corresponding height circles.
The above considerations can also be transferred to the case in which no terrain is heaped up, but rather removed . The resulting slope area can be understood as the envelope of the erosion cone. In this case, too, contour lines result as envelopes of height circles (the removal cone).
In books on descriptive geometry , slope areas are dealt with together with roof outlines under the heading of listed projections .
swell
- Fucke, Kirch, Nickel: Descriptive Geometry. Fachbuch-Verlag, Leipzig, 1998, ISBN 3-446-00778-4 , p. 139.
- Cornelie Leopold: Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart, 2005, ISBN 3-17-018489-X , p. 193.
Web links
- Descriptive geometry for civil engineers (PDF; 1.2 MB). Script (Uni Darmstadt)