In mathematics , an exponential function is a function of the form with a real number as the base (basic number). In the most common form, the real numbers are allowed for the exponent . In contrast to the power functions , in which the base is the independent quantity (variable) and the exponent is fixed, in the case of exponential functions the exponent (also exponent) of the power expression, the variable and the base are fixed. The naming also relates to this. Exponential functions have in the natural sciences , e.g. B. in the mathematical description of growth processes , an outstanding meaning (see exponential growth ).



As the exponential function in the strict sense (actually precise natural exponential ) refers to the exponential function , ie the exponential function with Euler number as the base; The spelling is also used for this . This function has special properties compared to the other exponential functions. Using the natural logarithm , the equation can be used to reduce any exponential function to such a base . Therefore, this article is mainly concerned with the exponential function of the base .






Sometimes a distinction is made in German between exponential functions (general) and the exponential function (for base e ).

Graph of the exponential function (red) with the tangent (light blue dashed line) through the point 0/1

definition
The exponential function to the base can be defined on the real numbers in different ways.

One possibility is the definition as a power series , the so-called exponential series
-
 ,
,
where denotes the factorial of .


Another possibility is the definition as a limit value of a sequence with :


Both types are also suitable for defining the complex exponential function on the complex numbers (see below).

The real exponential function is positive, continuous, strictly monotonically increasing and surjective . Here denotes the set of positive real numbers.


It is therefore bijective . This is why its inverse function , the natural logarithm, exists .

This explains the term antilogarithm for the exponential function.
Convergence of the series, continuity

The exponential function is continuous at 0.
The point-wise convergence of the series used to define the exponential function

can be shown for all real and complex simply with the quotient criterion; this even implies absolute convergence . The radius of convergence of the power series is therefore infinite. Since power series are analytical at every inner point of their convergence area, the exponential function is also trivially continuous in every real and complex point .

Calculation rules
Since the exponential function satisfies the functional equation, it can be used to generalize the exponentiation to real and complex exponents by defining:


for all and all real or complex .


In general, this transformation of also applies to any other values as a new basis:



Such functions are called exponential functions and “transform” multiplication into addition. The following laws show this more precisely:
-
 and
and 





These laws apply to all positive real and and all real and . Expressions with fractions and roots can often be simplified using the exponential function:





![\ sqrt [q] {a ^ p} = a ^ \ frac {p} {q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5f064b2b5c3a83176ec72959edc61a5c8347d5a)
See also calculation rules for logarithms .
Derivation
The great importance of the exponential function, i.e. the exponential function with basis , is based on the fact that its derivation results in the function itself:


If you additionally

demands, the e-function is actually the only function that performs this. Thus, one can also define the e-function as the solution of this differential equation f '(x) = f (x) with this initial condition f (0) = 1.

More generally it follows for real from


and the chain rule the derivation of arbitrary exponential functions:

In this formula, the natural logarithm cannot be replaced by a logarithm to any other base; the number e thus comes into play in a “natural” way in differential calculus.
Indefinite integral
From the results of the derivation, the results primitive function of the exponential function:
-
 .
.
For any exponential function with and the following applies:


-
 .
.
Exponential function on the complex numbers

Color-coded representation of the complex exponential function. Dark colors mean small functional values, light / faded colors mean large functional values. The base color represents the argument of the function value. This is the angle that the function value has relative to the real axis (viewpoint in the origin of coordinates). Positive real values appear red, negative real values appear turquoise. The repeating colored bands clearly show that the function is periodic in the imaginary direction.

Real part of the complex exponential function

Imaginary part of the complex exponential function
With the help of the series display

the exponential function for complex numbers can be defined. The series absolutely converges for all .


The exponential reserves for all complex numbers , the following important features:






The exponential function is thus a surjective but not injective group homomorphism from the Abelian group to the Abelian group , i.e. from the additive to the multiplicative group of the body .



In , the exponential function has an essential singularity , otherwise it is holomorphic , i.e. i.e., it is a whole function . The complex exponential function is periodic with the complex period , so it holds



If you restrict their domain to a strip

with , then it has a well-defined inverse function, the complex logarithm .

The exponential function can be used to define the trigonometric functions for complex numbers:


This is equivalent to Euler's formula
-
 .
.
The specific equation is derived from this

the complex exponential oscillation with angular frequency and frequency, which is important in physics and technology .


The exponential function can also be used to define the hyperbolic functions :



A general power can also be defined in the complex :
-
 with .
with .
The values of the power function depend on the choice of the single-leaf range of the logarithm, see also Riemann surface . Its ambiguity is caused by the periodicity of its inverse function, precisely the exponential function. Their basic equation

arises from the periodicity of the exponential function with real argument . Their period length is exactly the circumference of the unit circle, which the sine and cosine functions describe due to Euler's formula . The exponential, sine and cosine functions are only parts of the same exponential function (generalized to complex numbers), which is not obvious in the real world.



Exponential function on arbitrary Banach algebras
The exponential function can be generalized to Banach algebras , for example matrix algebras with an operator norm . She is there also over the series

which converges absolutely for all restricted arguments from the Banach algebra under consideration.
The essential property of the real (and complex) exponential function

In this generality, however, is only valid for values and , which commute , i.e. for values with (this is of course always fulfilled in real or complex numbers, since multiplication is commutative there). Some calculation rules of this kind for the exponentials of linear operators on a Banach space are provided by the Baker-Campbell-Hausdorff formulas .



An important application of this generalized exponential function is found in solving systems of linear differential equations of the form with constant coefficients. In this case the Banach algebra is the set of matrices with complex entries. Using the Jordanian normal form , a basis or similarity transformation can be found in which the exponential matrix has a finite calculation rule. More precisely, one finds a regular matrix such that , where are a diagonal matrix and a nilpotent matrix which commute with each other. It is valid with it







The exponential of a diagonal matrix is the diagonal matrix of the exponentials, the exponential of the nilpotent matrix is a matrix-valued polynomial with a degree that is smaller than the dimension of the matrix .


Numerical calculation options
As a fundamental function of analysis, much thought has been given to ways of efficiently calculating the exponential function up to the desired accuracy. The calculation is always reduced to the evaluation of the exponential function in a small area around zero and the beginning of the power series is used. In the analysis, the work accuracy required by the reduction must be weighed against the number of necessary multiplications of high-precision data.
The remainder of the -th partial sum has a simple estimate against the geometric series , which on

-
 at for everyone with leads.
at for everyone with leads.


The simplest reduction uses identity , i. H. to the given is determined, with a choice being made according to the accuracy considerations. Thus, will be in a certain working accuracy, calculated and fold squared: . is now reduced to the desired accuracy and returned as.









More efficient processes require that , better in addition, and ( Arnold Schönhage ) are available in any (according to specification) working accuracy. Then the identities can



-
 or
or 
can be used to transform to one out of the interval or a significantly smaller interval and thus to reduce or even avoid the more complex squaring.


![[-0 {,} 4 \,; \, 0 {,} 4]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f74042094692ac8b78800e0946dad319f884be10)
When implemented in hardware, suitable procedures are used for their needs, for example:
Background and evidence
motivation
The exponential function is encountered when trying to generalize the exponentiation to any real exponent. One starts with the calculation rule and therefore searches for a solution to the functional equation . If one now first of all assumes that a solution actually exists and calculates its derivative , one comes across the expression




What does now mean? If this limit value is called , then applies to through



defined number (or , must then ie the logarithm to the base to be) according to the chain rule formally





 then probably fulfilled
then probably fulfilled

How can you calculate this number ? Put purely formally and solve the equation


-
 , then you get . For the number
, then you get . For the number

so it can be assumed that

applies.
For you get the representation with purely formal



thus the one definition of the exponential function.
Taylor series
Alternatively, you can try the function

to develop into a Taylor series . Because by induction too

must apply, so one obtains for the Taylor series at the point


thus exactly the other definition of the exponential function. Then it has to be shown that the exponential function defined in this way actually has the desired properties. This Taylor series can also be represented as a continued fraction :

Convergence of the following representation
The sequence used to define the exponential function

is pointwise convergent for real , since it is firstly monotonically increasing from a certain index and secondly is bounded upwards .

Proof of monotony
From the inequality of the arithmetic and geometric mean it follows for
![\ begin {align} \ sqrt [n + 1] {\ left (1+ \ frac {x} {n} \ right) ^ n \ cdot 1} & \ leq \ frac {1} {n + 1} \ left (n \ left (1+ \ frac {x} {n} \ right) +1 \ right) \\ & = 1 + \ frac {x} {n + 1}, \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/870c8215b93e1c26628aa6869f83f4d131df782f)
the consequence is therefore monotonically increasing for almost all .

Proof of limitation
From the inequality of the harmonic and geometric mean it follows for
![\ begin {align} \ sqrt [n + 1] {\ left (1+ \ frac {x} {nx} \ right) ^ n \ cdot 1} & = \ sqrt [n + 1] {\ left (\ frac {n} {nx} \ right) ^ n \ cdot 1} \\ & \ geq \ frac {n + 1} {1 + n \ frac {nx} {n}} \\ & = 1 + \ frac {x } {n + 1-x}. \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e2995630ce72de35ae916dad504e49c3f7b214)
For and the consequence is therefore limited for all :




Obviously the bound holds
for and


Functional equation
Since and converge, their product also converges



If now , the Bernoulli inequality yields for sufficiently large

-
 ;
;
for is obtained from the inequality for, which is easy to show, and also the Bernoullian inequality for sufficiently large




the exponential function so effectively meets the functional equation .

Inequalities
Downward estimate
For real the exponential function can be written with


estimate downwards. The proof follows from the definition

and the fact that for sufficiently large . Since the sequence increases monotonically, the limit value is therefore really greater than zero.


This estimate can be turned into an important inequality

tighten. For it follows from , for the proof results, for example, by applying the Bernoulli inequality to the definition




applies. One application of this inequality is the polya-proof of the inequality of the arithmetic and geometric mean . However, the inequality of the arithmetic and geometric mean makes the investigation of the sequence much easier ; In order to avoid circular reasoning, the polya-proof requires derivations of the exponential function, which get by without inequality of the arithmetic and geometric mean.

Upward estimate
If, in the estimate down instead and used , we obtain by changing the inequality for all valid estimate upwards .






Derivation of the exponential function
The most important application of these two estimates is the calculation of the derivative of the exponential function at the point 0:

Together with the functional equation, the derivation of the exponential function for any real numbers follows:


Growth of the exponential function compared to polynomial functions
Often the statement is required that the exponential function grows much faster than any power function , i. H.

For this is clear, for either the rule of de l'Hospital can be used inductively , or elegantly estimated:


First of all,

because true


This converges to and thus the above limit value to 0.

Change of base
As mentioned earlier, the following applies

Proof: By definition of the logarithm is equivalent to , from which the identity follows. Replace with supplies






where in the second step the logarithm calculation rule for powers was applied.
The differential equation of the exponential function
If you want to solve the simple differential equation :
and still presuppose, you get a definition of .



Inverse function
If one does not assume, one uses the inverse function of



Because , and according to the properties of the logarithm function is


and the inverse function can be formed and obtained

Since the lower limit is 1, is and the inverse function on the property of the inverse function: .



Differential equation

The differential equation
y =
y ′ describes the relationship between a variable
y and its growth
y ′: both are equal. Therefore , the larger it is, the faster
y grows . The graphic shows an example of four solutions to this differential equation, with the exponential function e
x shown in red.
Extending the differential equation on for and resolves them, we obtain for the shape




Especially for is


Then is a solution and then is



and according to requirement

For any we carry


a. It turns out

and again after assumption

One now has an instrument for describing processes in various fields of science in which, by means of an approach of the type,
one obtains a result of the form which is based on the exponential function.


Examples of exponential functions
physics
Examples of the frequent occurrence of the exponential function in physics are:
chemistry
A simple chemical reaction is outlined here as an example in chemistry . It is assumed that we have the solution of a substance, such as cane sugar in water. The cane sugar is now converted to invert sugar ( hydrolyzed ) by a catalyst . For this simple chemical reaction, the rate law (neglecting the reverse reaction ) will be formulated as follows:
-
The rate of reaction as a function of time is proportional to the amount of the transforming substance still present .
If we denote the amount of cane sugar that has not yet been converted
, then the reaction rate is , and according to the rate law formulated above, the equation applies




with a reaction-specific rate constant . From this momentary approach one obtains an integral law according to the above differential equation, which gives us the amount of remaining cane sugar as a function of time:



where the constant denotes the amount currently available. The chemical reaction thus
approaches its final state asymptotically , the complete conversion of cane sugar into invert sugar. (Neglecting the reverse reaction is acceptable here, since the chemical equilibrium of the cane sugar hydrolysis is very much on the side of the invert sugar).



Biology, epidemics

Cases of illness and death (black) in the course of the Ebola fever epidemic in West Africa up to July 2014 (approximate logistical function)
The exponential function is only useful for describing the growth of a population of z. B. microorganisms (see. R-strategy ), the reproduction of other living beings or for the spread of infections in the context of an epidemic . Then the increase is more meaningfully described with the logistic function , cf. the adjacent graphic of the spread of Ebola in West Africa in 2014.
Stochastics
- Same number of coins and receivers
What are the probabilities randomly to receive any one or more coins when coins happen to be distributed receiver and is very large?



The definition formula for the exponential function
-
 ,
,
the approximation formula derived from it

and Euler's number
allow a simple estimate.

The probability of receiving a coin the first time it is distributed is and of not receiving a coin. The chance to get twice no coin is: . Hence the probability of being unsuccessful times is:





The probability of only being successful once is the product of failure, success and the possible combinations when success occurs (the first time, or the second or third ...):


The probability of getting more than one coin is accordingly:

- More coins than recipients
How many coins do you need to reduce the probability of not receiving any, for example to 0.1 instead of 0.37? From the above approximation formula follows:



Or to put it another way: How many coins does it have to be more than a recipient ?



So that on average only 10% of the recipients go empty-handed, 2.3 times the amount of coins is required, with 1% almost 5 times the amount.
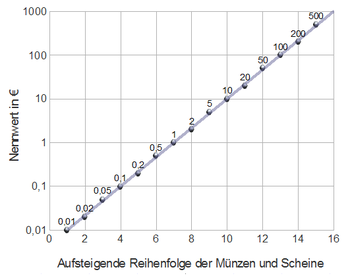
Logarithmic representation of the nominal value of the euro
economy
- Continuous interest
- The denomination usually follows an exponential law as the value increases. Using the euro as an example, a best-fit line is shown for the points for each coin or banknote. The slight deviations from this straight line result from the requirement for "round" numbers that are to be specified precisely with only one significant digit (not to be confused with even numbers ).
Generalizations
If there is a quantity whose powers exist for any non-negative integer , and if the limit value exists, it makes sense to define the abstract quantity by the exponential series given above. The same applies to operators that, including their powers, result in a linear mapping of a domain of definition of an abstract space (with elements ) into a domain of real numbers: Here it is even useful for all real numbers , in very (more precisely: in the associated closing area) exponential operators to be defined by the expression
, the convergence of this expression initially remaining open.













Iterating exponentiation results in the generalized exponential function used in floating point arithmetic .
Individual evidence
-
^ Christian Blatter, Analysis II . 1st edition, Springer Verlag 1974, ISBN 3-540-06914-3 , chap. 18, § 182, power series
-
↑ Konrad Knopp. Theory and Application of Infinite Series . 5th edition, Springer Verlag 1964, ISBN 3-540-03138-3 . S 175, 98 sentence 2 for the real and S 418 for the complex case
-
↑ Lorentzen, L .; Waadeland, H. (2008). "A.2.2 The exponential function." . Continued Fractions . Atlantis Studies in Mathematics. p. 268. doi : 10.2991 / 978-94-91216-37-4 .
See also
Web links








































![\ sqrt [q] {a ^ p} = a ^ \ frac {p} {q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5f064b2b5c3a83176ec72959edc61a5c8347d5a)
































































![[-0 {,} 4 \,; \, 0 {,} 4]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f74042094692ac8b78800e0946dad319f884be10)


























![\ begin {align} \ sqrt [n + 1] {\ left (1+ \ frac {x} {n} \ right) ^ n \ cdot 1} & \ leq \ frac {1} {n + 1} \ left (n \ left (1+ \ frac {x} {n} \ right) +1 \ right) \\ & = 1 + \ frac {x} {n + 1}, \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/870c8215b93e1c26628aa6869f83f4d131df782f)

![\ begin {align} \ sqrt [n + 1] {\ left (1+ \ frac {x} {nx} \ right) ^ n \ cdot 1} & = \ sqrt [n + 1] {\ left (\ frac {n} {nx} \ right) ^ n \ cdot 1} \\ & \ geq \ frac {n + 1} {1 + n \ frac {nx} {n}} \\ & = 1 + \ frac {x } {n + 1-x}. \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e2995630ce72de35ae916dad504e49c3f7b214)

































































































