Logarithmic spiral

The following important information is missing from this article or section:

Evidence / references

Help Wikipedia by researching and pasting it .

Logarithmic spiral, clockwise

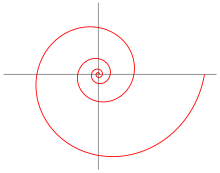
A logarithmic spiral is a spiral in which the distance from this center changes by the same factor with each revolution around its center (center, pole ). The radius increases proportionally to the arc or spiral length. Every straight line through the pole always intersects the logarithmic spiral at the same angle (see isogonal trajectory ). Because of this property, one speaks of an equiangular spiral . This property clearly characterizes the logarithmic spiral.

It can be proven that René Descartes first discussed the logarithmic spiral in letters to Marin Mersenne in 1638 .

Mathematical representation

Every logarithmic spiral can easily be specified in polar coordinates . For describes the equation ${\displaystyle (r(\varphi ),\varphi )}$ ${\displaystyle a,k\in \mathbb {R} \setminus \{0\}}$

${\displaystyle \quad r(\varphi )=ae^{k\varphi },\quad \varphi \in \mathbb {R} ,}$

a function , and by means of the polar coordinate interpretation a logarithmic spiral in the Euclidean plane. The parameter is called the slope of the spiral . This can also be expressed by, in which case the slope angle is called. This is not the tangent angle drawn below ! ${\displaystyle r\colon \mathbb {R} \to \mathbb {R} }$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle \tan \alpha }$ ${\displaystyle \alpha \in \left]-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right[}$

In Cartesian coordinates we get:

${\displaystyle x(\varphi )=r(\varphi )\cos {\varphi }=ae^{k\varphi }\cos {\varphi }}$

${\displaystyle y(\varphi )=r(\varphi )\sin {\varphi }=ae^{k\varphi }\sin {\varphi }}$

It is named after the representation in which the angle is expressed as a function of the radius : ${\displaystyle r}$

${\displaystyle \varphi (r)={\frac {1}{k}}\ln \left({\frac {r}{a}}\right)\quad ,}$and this free parameter (of the equation) is off if and off if . ${\displaystyle r}$ ${\displaystyle \mathbb {R} ^{+}}$ ${\displaystyle a>0}$ ${\displaystyle \mathbb {R} ^{-}}$ ${\displaystyle a<0}$

In the complex plane , each logarithmic spiral can be represented even more simply.

With and applies: ${\displaystyle z\in \mathbb {C} \setminus \mathbb {R} }$ ${\displaystyle \left|z\right|\neq 1}$

${\displaystyle w(t)=az^{t},\quad t\in \mathbb {R} ,}$

for is the polar form of , then applies ${\displaystyle z=|z|e^{i\arg z}}$ ${\displaystyle z}$

${\displaystyle z^{t}=|z|^{t}e^{it\arg z}=e^{t\ln |z|}\left(\cos \left(t\arg z\right)+i\sin \left(t\arg z\right)\right)}$.

So this happens with the two (analytical) bijections and , because according to assumption. ${\displaystyle \varphi \mapsto t\arg z}$ ${\displaystyle k\mapsto {\tfrac {\ln |z|}{\arg z}}}$ ${\displaystyle \arg z\neq 0}$

Another simple representation from the differential geometry of plane curves is:

Only if for (arbitrary, but fixed) for all real values the differential equation ${\displaystyle k\in \mathbb {R} }$ ${\displaystyle \varphi }$

${\displaystyle {\tfrac {1}{r}}{\tfrac {\mathrm {d} }{\mathrm {d} \varphi }}r=k}$

holds, then the associated set of points (in polar coordinates) is called a logarithmic spiral with a slope (parameter) . ${\displaystyle (r(\varphi ),\varphi )\in \mathbb {R} ^{2}}$ ${\displaystyle k}$

properties

Logarithmic spiral: all straight lines passing through the pole intersect the curve at the same tangent angle

The logarithmic spiral has a number of unique properties, which is why one of her greatest lovers, Jakob I Bernoulli , also referred to it as spira mirabilis ("miraculous spiral"):

• The sign of shows the clear direction of rotation of the spiral in the plane. ${\displaystyle ak}$
• All straight lines going through the pole intersect the curve - i.e. their tangents - at the same tangent angle with and therefore (see illustration). One can even demand this as a property and thus define logarithmic spirals (see their representation in the form of a differential equation). ${\displaystyle {\bar {\alpha }}}$ ${\displaystyle \tan {\bar {\alpha }}={\tfrac {1}{k}}=\cot \alpha }$ ${\displaystyle {\bar {\alpha }}={\tfrac {\pi }{2}}-\alpha }$
• The spiral circles the origin infinitely often without reaching it ( asymptotic point ).
• Although the curve does not reach the pole, which it orbits "infinitely" often, for any finite angle value, the arc length from each curve point to the pole is finite and amounts to . ${\displaystyle s(\varphi )=a{\tfrac {\sqrt {1+k^{2}}}{k}}e^{k\varphi }}$
• With each turn the radius increases by a constant factor:

${\displaystyle r(\varphi +2\pi )=ae^{k(\varphi +2\pi )}=ae^{k\cdot 2\pi }e^{k\varphi }=(e^{2\pi })^{k}r(\varphi )}$

with e ^2π  ≈ 535.5 to a power of the slope k (therefore only relatively flat spirals with k  ≪ 1 result in “pretty” snails). This property distinguishes all logarithmic spirals from the Archimedean ones , which expand by a constant with every turn (their pitch decreases).

• The logarithmic spiral is - as a generalization of the above derivation - self-similar (invariant) compared to a centric stretching by the factor with simultaneous rotation by the angle . ${\displaystyle e^{k\gamma }}$ ${\displaystyle \gamma }$

This does not apply to the constantly growing Archimedes ' spiral : This is why rotating Archimedes' spirals seem to move "outwards", but logarithmic perspectives towards the observer.

• The curve is its own evolution .
• The curve is its own focal line ( caustic ) .
• The curve is its own base point curve .
• An inversion of the curve ( ) leads to a rotation and mirroring of the curve on the Y-axis (for mirroring only ); a left-hand logarithmic spiral becomes a right-hand one and vice versa. ${\displaystyle r\mapsto {\tfrac {1}{r}}}$ ${\displaystyle |a|=1}$
• All spirals with the same pitch are similar .
• For , the spiral approaches more and more a circle with a radius that fulfills the curve equation for ( angle of intersection 90 ° = ). Therefore one can also allow in the definition of the spiral and consider the circle as a special case of the logarithmic spiral, which is particularly important in spherical geometry . ${\displaystyle {k\to 0}\ }$ ${\displaystyle a}$ ${\displaystyle k=0}$ ${\displaystyle {\tfrac {\pi }{2}}}$ ${\displaystyle k=0}$
• The logarithmic spiral is a W-curve in the sense of projective geometry: it is invariant under a 1-parametric group of projective transformations .

Special cases and approximations

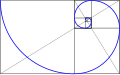
The golden spiral is a special case of the logarithmic spiral. This spiral can be constructed by recursively dividing a golden rectangle into a square and another, smaller golden rectangle (see following picture). For her, the golden ratio applies . ${\displaystyle k={\tfrac {4\ln(\Phi )}{2\pi }}}$ ${\displaystyle \Phi ={\tfrac {{\sqrt {5}}+1}{2}}}$

Every logarithmic spiral can also be approximated by a polygon . For its construction triangles with the same angle of inclination and the shorter side as long as the longer side of the previous triangle are lined up. An extension of this train of thought also applies to certain irregular polygons that can be placed next to one another. This construction principle is widespread in nature and generally produces multiple spirals .

• 

  Golden spiral

• 

  irregular polygon spiral

Formulas

see also: Formula collection geometry

Formulas for the logarithmic spiral
function	${\displaystyle r(\varphi )=a\cdot e^{k\cdot \varphi }\quad ,\quad \varphi (r)={\frac {1}{k}}\cdot \ln \left({\frac {r}{a}}\right)}$
pitch	${\displaystyle {\frac {1}{r}}\cdot {\frac {\mathrm {d} r}{\mathrm {d} \varphi }}=k=\tan(\alpha )}$
Radius of curvature	${\displaystyle \rho (r)=r\cdot {\sqrt {1+k^{2}}}={\frac {r}{\cos(\alpha )}}}$
Arc length	${\displaystyle s(r_{1})-s(r_{2})={\sqrt {1+k^{2}}}\cdot {\frac {r_{1}-r_{2}}{k}}={\frac {r_{1}-r_{2}}{\sin(\alpha )}}}$
Area	${\displaystyle A(r_{1})-A(r_{2})={\frac {r_{1}^{2}-r_{2}^{2}}{4k}}}$

Logarithmic spiral and loxodrome

Starting from a logarithmic spiral in the plane with the coordinate origin as its asymptotic point, a loxodrome can be constructed on a spherical surface. For this purpose, the curve is projected onto a spherical surface by placing a sphere with an arbitrary radius on the coordinate origin. This contact point is the south pole on the sphere. From the points of the logarithmic spiral in the plane rays are viewed through this sphere to the north pole of the sphere. These rays then define a new spherical curve when the spherical surface is cut for the first time. Straight lines that go through the origin in the plane become circles of length on the sphere and the flat logarithmic spiral describes a loxodrome on the spherical surface. Conversely, a suitable (north pole and south pole are the asymptotic points of the loxodrome) projection of a loxodrome from the sphere into the plane there creates a logarithmic spiral. This type of conformal projection of the sphere on the plane is called stereographic projection .

Occurrence

In living nature there are numerous examples of logarithmic spirals with various gradients, such as snail shells created by growth or the arrangement of kernels in the flower of a sunflower , or the inflorescence of a cauliflower variety called Romanesco Brassica Oleracea.

A flying insect orients itself during a night flight by the position of the (distant) moon by keeping the angle to it constant. However, the trajectory is regularly corrected by a (point near) street lamp so that it becomes a logarithmic spiral with the street lamp in the center.

In addition, almost logarithmic spiral structures can be found in dynamic multi-body systems and fluid dynamic systems ( vortex formation with a sufficiently large speed gradient) as well as in technology (e.g. back turning ).

• 

  Sunflower with 34 left-hand and 55 right-hand Fibonacci spirals

• 

  Section of a Nautilus bowl

• 

  Whirlpool galaxy , a typical spiral galaxy

• 

  Low pressure eddy over Iceland in Sep. Photographed in 2003 from an altitude of approx. 700 km

According to legend, it was a wish of the mathematician Jakob I Bernoulli , who dealt a lot with the logarithmic spiral, that his beloved logarithmic spiral should be carved on his tombstone with the inscription eadem mutata resurgo ("I return as the same") . After Bernoulli's death, the responsible stonemason chiseled a spiral on Bernoulli's tombstone, but it was an Archimedean spiral (presumably out of ignorance or to save work) for which none of the above properties apply. Bernoulli's tombstone can still be viewed today in the cloister of the cathedral in Basel .

Web links

Commons : Logarithmic spiral  - collection of images, videos, and audio files

• Eric W. Weisstein : Logarithmic Spiral . In: MathWorld (English).