Geometry formulary

${\displaystyle {\sqrt[{n}]{x}}}$

This article is a collection of formulas on the subject of geometry . Math symbols are used, which are explained in the article List of Math Symbols .

The formula collection for Euclidean geometry is part of the formula collection , which also contains formulas from the other departments.

Identifiers and spellings

In the vast majority of cases:

1. Points are labeled with Latin capital letters . ${\displaystyle (A,B,C,\ldots )}$
2. Lines such as straight lines, segments and arcs are labeled with Latin lowercase letters . ${\displaystyle (a,b,c,\ldots )}$
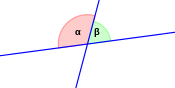
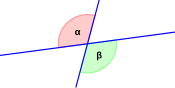
3. Angles are labeled with lowercase Greek letters . ${\displaystyle (\alpha ,\beta ,\gamma ,\ldots )}$

In the following, angles are given in degrees.

Geometry in the plane

Basics

angle

Secondary angle The sum of the secondary angles is always 180 °. ${\displaystyle \alpha +\beta =180^{\circ }}$
Vertex angle The vertex angles are always the same. ${\displaystyle \alpha =\beta }$
Step angle Step angles at cut parallels are always the same size.
Alternating angle Alternating angles at cut parallels are always the same size.
Exterior angle In the triangle, an exterior angle is equal to the sum of the two non-adjacent interior angles.
Sums of angles The sum of the interior angles in a triangle is always 180 ° The sum of the interior angles in a corner is always ${\displaystyle n}$ ${\displaystyle (n-2)\cdot 180^{\circ }}$ The sum of the exterior angles in a convex corner is always 360 ° (regardless of the number of corners ) ${\displaystyle n}$ ${\displaystyle n}$

Division of a route

Ratio division: In order to divide a line in a certain ratio (into equal parts), one first draws an arbitrary ray from which is not parallel to . On this one can cover any length of distance. Connect the end point obtained with and draw the parallels to through the points created when dividing . Their intersections with parts in equal parts. ${\displaystyle AB}$ ${\displaystyle n}$ ${\displaystyle A}$ ${\displaystyle AB}$ ${\displaystyle n}$ ${\displaystyle C}$ ${\displaystyle B}$ ${\displaystyle BC}$ ${\displaystyle AC}$ ${\displaystyle AB}$ ${\displaystyle AB}$ ${\displaystyle n}$

Areas and perimeters

A triangle with a standard name

The standard name for triangles:

Cornerstones

${\displaystyle A,B}$and . The corner is the meeting point of the same sides in the isosceles triangle and the vertex of the right angle in the right triangle . ${\displaystyle C}$ ${\displaystyle C}$

pages

${\displaystyle a}$is the side opposite the corner , the same applies to and . In the case of an equilateral triangle, all sides are marked with . ${\displaystyle A}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle a}$

angle

${\displaystyle \alpha }$is the (inside) angle in the corner , the angle in the corner and the angle in the corner . ${\displaystyle A}$ ${\displaystyle \beta }$ ${\displaystyle B}$ ${\displaystyle \gamma }$ ${\displaystyle C}$

figure	Area A	Scope U	Comment, other
triangle
General triangle	${\displaystyle {\frac {1}{2}}gh={\frac {1}{2}}bc\sin \alpha }$ ${\displaystyle ={\frac {abc}{4R}}=k\cdot r}$ ${\displaystyle ={\sqrt {k(k-a)(k-b)(k-c)}}}$	${\displaystyle a+b+c}$	The latter formula is called Heron's theorem. is half the circumference, the circumferential radius and the incircle radius. ${\displaystyle k}$ ${\displaystyle R}$ ${\displaystyle r}$
Equilateral triangle	${\displaystyle {\frac {1}{4}}a^{2}{\sqrt {3}}}$	${\displaystyle 3\cdot a}$	All pages are the same length. All angles are the same size (60 °). Contour lines = axes of symmetry = bisector = bisector = median normal
Isosceles triangle	${\displaystyle {\frac {1}{2}}c{\sqrt {a^{2}-{\frac {1}{4}}c^{2}}}}$	${\displaystyle 2a+c}$	Two sides are the same length ( legs and ); the third side is called the base. The two base angles ( and ) are equal. The contour line through bisects the angle and the base . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle C}$ ${\displaystyle \gamma }$ ${\displaystyle c}$
Right triangle	${\displaystyle {\frac {1}{2}}ab}$	${\displaystyle a+b+c}$	${\displaystyle \gamma =\alpha +\beta =90^{\circ }}$. Hypotenuse = longest side = side opposite the 90 ° angle. Cathets = sides that form a right angle. The sentence group of Pythagoras applies (see below)
square
square	${\displaystyle a^{2}}$	${\displaystyle 4\cdot a}$	diagonal ${\displaystyle d=a\cdot {\sqrt {2}}}$
rectangle	${\displaystyle a\cdot b}$	${\displaystyle 2\cdot (a+b)}$	diagonal ${\displaystyle d={\sqrt {a^{2}+b^{2}}}}$
Lozenge (diamond)	${\displaystyle {\frac {1}{2}}ef=a^{2}\cdot \sin \alpha }$	${\displaystyle 4\cdot a}$	${\displaystyle e,f}$= Diagonals, = any interior angle. ${\displaystyle \alpha }$
parallelogram	${\displaystyle a\cdot h_{a}}$	${\displaystyle 2\cdot (a+b)}$	${\displaystyle h_{a}}$is the height to the side . ${\displaystyle a}$
Trapezoid	${\displaystyle m\cdot h={\frac {1}{2}}(a+c)\cdot h}$	${\displaystyle a+b+c+d}$	${\displaystyle a,c}$= parallel sides, = center line ${\displaystyle m={\tfrac {1}{2}}(a+c)}$
symmetrical kite (deltoid)	${\displaystyle {\frac {1}{2}}ef}$	${\displaystyle 2\cdot (a+b)}$	${\displaystyle e,f}$ = Diagonals.
Tendon quadrangle	${\displaystyle {\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$ ${\displaystyle ={\frac {e\cdot (ab+cd)}{4R}}={\frac {f\cdot (ad+bc)}{4R}}}$	${\displaystyle a+b+c+d}$	Square with perimeter , perimeter radius , half perimeter; Diagonal: , ${\displaystyle R}$ ${\displaystyle ={\frac {1}{4A}}{\sqrt {(ab+cd)(ac+bd)(ad+bc)}}}$ ${\displaystyle s}$ ${\displaystyle e,f}$ ${\displaystyle e={\sqrt {\frac {(ac+bd)(ad+bc)}{ab+cd}}}}$ ${\displaystyle f={\sqrt {\frac {(ab+cd)(ac+bd)}{ad+bc}}}}$
Tangent square	${\displaystyle r\cdot (a+c)=r\cdot (b+d)}$	${\displaystyle a+b+c+d}$	Quadrilateral with an incircle with an incircle radius . It applies ${\displaystyle r}$ ${\displaystyle a+c=b+d}$
Polygons
Regular polygon	${\displaystyle {\frac {n\cdot r_{\mathrm {u} }^{2}\cdot \sin {\frac {360^{\circ }}{n}}}{2}}}$ ${\displaystyle =n\cdot r_{\mathrm {i} }^{2}\cdot \tan {\frac {180^{\circ }}{n}}}$ ${\displaystyle ={\frac {n\cdot l_{\mathrm {k} }^{2}\cdot \cot {\frac {180^{\circ }}{n}}}{4}}}$	${\displaystyle 2\cdot n\cdot r_{\mathrm {u} }\cdot \sin {\frac {180^{\circ }}{n}}}$ ${\displaystyle =2\cdot n\cdot r_{\mathrm {i} }\cdot \tan {\frac {180^{\circ }}{n}}}$ ${\displaystyle =n\cdot l_{\mathrm {k} }}$	${\displaystyle n}$ - number of corners ${\displaystyle r_{u}}$- radius of the perimeter, d. H. Distance from the center to a corner ${\displaystyle r_{i}}$- the radius of the inscribed circle, d. H. Distance from the center to a center of a page ${\displaystyle l_{k}}$ - Edge length of one side of the polygon
circle
circle	${\displaystyle \pi \cdot r^{2}={1 \over 4}\cdot \pi \cdot d^{2}}$	${\displaystyle 2\cdot \pi \cdot r=\pi \cdot d}$	It denotes the circle number . ${\displaystyle \pi =3{,}14159\ldots }$
Circular ring	${\displaystyle \pi \cdot (R^{2}-r^{2})}$	${\displaystyle 2\cdot \pi \cdot (R+r)}$	${\displaystyle R}$= Outer radius, = inner radius ${\displaystyle r}$
Section of a circle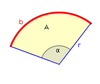	${\displaystyle \pi \cdot r^{2}\cdot {\alpha \over 360^{\circ }}={\frac {1}{2}}r^{2}\cdot \varphi }$ ${\displaystyle ={\frac {1}{2}}\cdot b\cdot r}$	${\displaystyle \pi \cdot r\cdot {\alpha \over 180^{\circ }}+2r=r(\varphi +2)}$	b = (angle in radians) ${\displaystyle \pi \cdot r\cdot {\alpha \over 180^{\circ }}=r\cdot \varphi ;\quad \varphi =\alpha \cdot {\frac {\pi }{180^{\circ }}}}$
Circle segment	${\displaystyle {\frac {1}{2}}r^{2}\cdot (\varphi -\sin \varphi )}$	${\displaystyle r\cdot \left(2+{\sqrt {2-2\cos \varphi }}\right)}$	${\displaystyle \varphi =\alpha \cdot {\frac {\pi }{180^{\circ }}}}$ (Angle in radians)
Conic sections
ellipse	${\displaystyle \pi ab}$ ${\displaystyle ={\frac {1}{4}}\pi \cdot D\cdot d}$	${\displaystyle 4a\int \limits _{0}^{\frac {\pi }{2}}{\sqrt {1-\varepsilon ^{2}(\sin t)^{2}}}\ \mathrm {d} t=4a\;E(\varepsilon )}$	Set of points for which the sum of the two distances to two given points (focal points) is constant ( ). The scope cannot be specified with elementary functions (→ elliptic integral). D, d large and small diameter. Cartesian coordinates: ${\displaystyle 2a}$ ${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
hyperbole	No closed area	Not a closed curve	Set of all points for which the absolute difference between the distances to the focal points is constant 2a. Cartesian coordinates: ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
parabola	No closed area	Not a closed curve	Set of all points whose distance to a special fixed point (the focal point) and a special straight line (the guide line l) is constant. Cartesian coordinates: . ${\displaystyle y^{2}=2px\,}$

Triangle geometry

Excellent points

Side bisector and focus

• Side bisector (median lines)
  • share each other in a ratio of 2: 1.
  • intersect at a point, the center of gravity S of the triangle.
  • divide the triangular area into two equally large partial areas.

• Intersection of the perpendicular lines ( mid-normals ) = center of the circumference .

Bisector and inscribed circle

• Intersection of the bisector = center of the inscribed circle .

Heights

• Contour lines
  • intersect at a point H, the intersection of the triangle.
  • The height h _c is the normal distance from point C to side c (right angle at D).

Pythagorean sentence group

• Pythagorean theorem

  In a right triangle, the area of ​​the square above the hypotenuse is equal to the sum of the areas of the squares above the cathetus.
  If and are the lengths of the cathetus and the length of the hypotenuse, then: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

  ${\displaystyle a^{2}+b^{2}=c^{2}\,}$

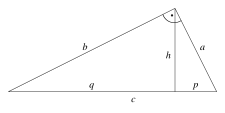
• Catheter set

  In the right-angled triangle, the square above a cathetus is equal in area to the rectangle from the hypotenuse and the projection of this cathete onto the hypotenuse.
  The following applies to the designations in the drawing below:

  ${\displaystyle a^{2}=p\cdot c,\ b^{2}=q\cdot c}$

• Altitude rate

  In the right-angled triangle, the square above the height on the hypotenuse has the same area as the rectangle from the hypotenuse sections.
  The following applies to the designations in the drawing below:

  ${\displaystyle h^{2}=q\cdot p}$

  

Triangle inequality

The sum of two sides of a triangle is always greater than the third side.

Congruence and Similarity Theorems

Two triangles are congruent or congruent if they match in

1. three sides (sss)
2. two sides and the included angle (sws)
3. two sides and the opposite angle of the longer side (Ssw)
4. one side and the two adjacent angles (wsw)

Two triangles are similar , though

1. three pairs of corresponding sides have the same ratio
2. two pairs of corresponding sides have the same ratio and the angles enclosed by these sides match
3. two pairs of corresponding sides have the same ratio and the opposite angles of the longer sides match
4. match two angles

Ray theorems

1. Theorem of rays: If a two-ray is intersected by two parallel straight lines, the ray sections of the first ray are in the same ratio as the corresponding sections of the second ray.
2. Theorem of rays: If a two-ray is intersected by two parallel straight lines, the parallel sections are in the same ratio as the associated ray sections measured from the apex on the same ray.

Geometry of the body

body	Volume V	Surface O	Comments, other
Prisms
Parallelepiped (spat)	${\displaystyle G\cdot h}$	${\displaystyle 2\cdot (ah_{a}+bh_{b}+ch_{c})}$
Cuboid	${\displaystyle a\cdot b\cdot c}$	${\displaystyle 2\cdot (ab+ac+bc)}$	Room diagonal length ${\displaystyle ={\sqrt {a^{2}+b^{2}+c^{2}}}}$
General prism	${\displaystyle A_{G}\cdot h}$	${\displaystyle 2A_{G}+A_{M}\,}$	${\displaystyle A_{M}}$ Outer surface
columns
Round column ( cylinder )	${\displaystyle \pi \cdot r^{2}\cdot h}$	${\displaystyle 2\pi r\cdot (r+h)}$
Hollow cylinder	${\displaystyle \pi R^{2}h-\pi r^{2}h=\,}$ ${\displaystyle \pi h(R+r)(R-r)\,}$	${\displaystyle 2\pi ((R+r)h+R^{2}-r^{2})\,}$	${\displaystyle R,r}$ Outside, inside radius ${\displaystyle M_{\text{aussen}}=2\pi Rh}$ ${\displaystyle M_{\text{innen}}=2\pi rh}$
pyramid
General pyramid	${\displaystyle {\frac {1}{3}}A_{G}h}$	${\displaystyle A_{G}+A_{M}\,}$
Truncated pyramid	${\displaystyle {\frac {1}{3}}h\left(A_{G}+{\sqrt {A_{G}A_{D}}}+A_{D}\right)}$	${\displaystyle A_{G}+A_{D}+A_{M}\,}$	${\displaystyle A_{G}}$Base area top area ${\displaystyle A_{D}}$
cone
Circular cone	${\displaystyle {\frac {1}{3}}\cdot \pi \cdot r^{2}\cdot h}$	only for vertical cones: ${\displaystyle r\cdot \pi \cdot (r+s)}$	Relationship between radius, height and side height: ${\displaystyle s^{2}=r^{2}+h^{2}\,}$
straight truncated cone	${\displaystyle {\frac {1}{3}}\pi h(r_{1}^{2}+r_{1}r_{2}+r_{2}^{2})}$	${\displaystyle A_{G}+A_{D}+A_{M}\,}$ ${\displaystyle =\pi r_{2}^{2}+\pi r_{1}^{2}+\pi s(r_{1}+r_{2})}$	${\displaystyle s=\mathrm {Mantellinie} ={\sqrt {(r_{2}-r_{1})^{2}+h^{2}}}}$ ${\displaystyle r_{1},r_{2}}$ Radii
Platonic solids
Tetrahedron	${\displaystyle {\frac {1}{12}}a^{3}{\sqrt {2}}}$	${\displaystyle a^{2}{\sqrt {3}}}$
Hexahedron (cube)	${\displaystyle a^{3}\,}$	${\displaystyle 6\cdot a^{2}}$	Room diagonal length ${\displaystyle =a{\sqrt {3}}}$
octahedron	${\displaystyle {\frac {1}{3}}a^{3}{\sqrt {2}}}$	${\displaystyle 2a^{2}{\sqrt {3}}}$
Dodecahedron	${\displaystyle {\frac {1}{4}}a^{3}(15+7{\sqrt {5}})}$	${\displaystyle 3a^{2}{\sqrt {25+10{\sqrt {5}}}}}$
Icosahedron	${\displaystyle {\frac {5}{12}}a^{3}(3+{\sqrt {5}})}$	${\displaystyle 5a^{2}{\sqrt {3}}}$
Ball and ball parts
Bullet	${\displaystyle {4 \over 3}\cdot \pi \cdot r^{3}={1 \over 6}\cdot \pi \cdot d^{3}}$	${\displaystyle 4\cdot \pi \cdot r^{2}=\pi \cdot d^{2}}$
Spherical cap ( spherical cap , spherical cap)		${\displaystyle 2\cdot r\cdot \pi \cdot h}$
Spherical segment ( spherical segment )	${\displaystyle {h^{2}\cdot \pi \over 3}\cdot (3r-h)}$	${\displaystyle 2\cdot r\cdot \pi \cdot h+\rho ^{2}\pi }$	With ${\displaystyle \rho ^{2}=h\cdot (2r-h)}$
Spherical zone ( spherical layer )	${\displaystyle {\frac {1}{6}}\pi \cdot h(3\cdot a^{2}+3\cdot b^{2}+h^{2})}$	${\displaystyle \pi \cdot (2\cdot r\cdot h+a^{2}+b^{2})}$	with = diameter of the lower cutting circle and = diameter of the upper cutting circle ${\displaystyle 2\cdot a}$ ${\displaystyle 2\cdot b}$
Rotating body
Ellipsoid	${\displaystyle {\frac {4}{3}}\cdot \pi \cdot a\cdot b\cdot c\,}$		Semi-axes a, b, c
Torus	${\displaystyle 2\pi ^{2}\cdot R\cdot r^{2}}$	${\displaystyle 4\pi ^{2}\cdot R\cdot r}$

see also: Euler's polyhedron substitution , Cavalieri's principle

trigonometry

see: Trigonometry , Trigonometry formula collection

Analytical geometry

see: Analytical Geometry , collection of formulas for analytical geometry