Pythagorean sentence group
The Pythagorean sentence group includes three sentences of mathematics that deal with calculations in right triangles :
- Pythagorean Theorem (Euclid: Elements , Book I, § 47 and Book VI, § 31)
- Euclid's set of cathets (Euclid: elements , book I, § 47)
- Height theorem of Euclid (Euclid: elements , Book VI - § 8, Book II - § 14 (implicit))
The individual sentences
Pythagorean theorem
In a right triangle, the area of the square above the hypotenuse is equal to the sum of the areas of the squares above the two cathets.
- Let be the sides of the right triangle, where let be the hypotenuse. The square over has the same area as the sum of the squares over and .
As a formula:
Euclid's set of cathets
The extension of the perpendicular erected above the hypotenuse of the right-angled triangle ( height of the triangle) divides the square above the hypotenuse into two rectangles. The cathetus set says that one of the rectangles has the same area as one of the squares above the two cathets.
- Let be the sides of the right triangle, where let be the hypotenuse. The plumb line divides the hypotenuse into segments and . The following applies:
- The square above is the same area as the rectangle with sides and , and the square above is the same area as the rectangle with sides and .
As formulas:
Euclid's theorem of elevation
The theorem of heights says that in a right-angled triangle the square above the height has the same area as the rectangle from the hypotenuse sections. Or:
- Are the sides of the right triangle and and those parts of the hypotenuse , which by their pitch at the nadir point to the height formed. Then
- .
The reverse is also true:
- If the height theorem applies in a triangle, then this triangle is right-angled.
proofs
There are many different proofs for the Pythagorean Theorem , see article Pythagorean Theorem . From this one can prove the height theorem and the cathetus theorem by algebraic calculation, but also the other way round, the Pythagorean theorem follows from each of these two theorems! The three sentences are therefore equivalent : If one of the three sentences is proven, the other two sentences in the sentence group are also valid.
Algebraic Proofs
Proof of the theorem of heights
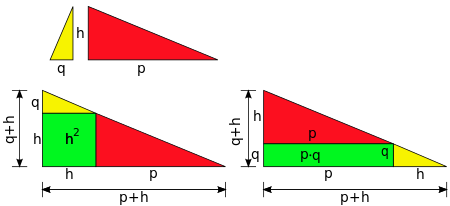
The proof of the theorem of heights can be done with the Pythagorean theorem and the binomial formula .
In the diagram you can see three right-angled triangles, one with the sides , then one with and . The Pythagorean theorem applies to each of these triangles:
Also applies . So the square is:
- .
According to the first binomial formula, this is
- .
If you insert this for in the first formula and for and the respective left part of the second and third formula, you get:
and with it . After dividing by two, we get the height theorem to be proven:
- .
Proof of the catheter set
This proof is analogous to the proof of the height theorem using the above four formulas: It is
and thus
analogously then applies
- .
Proof of the cathetus set with the help of the height theorem
Referring to the graphic in the proof of the height theorem:
Geometric evidence
There is also geometric evidence for the height theorem and the cathetus set:
Supplementary proof of the height theorem
Two right triangles are congruent if the cathets are the same (the included angle is also the same).
If you divide a right-angled triangle at the height into two right-angled triangles with the sides and or and (yellow and red triangles in the diagram), you can connect them to a square with the side length (in the diagram below left) and to a rectangle with the Pages and create (in the diagram below right).
In both cases a right-angled triangle is created with the cathets and . The right and left triangles are therefore congruent. The first consists of the yellow and red triangles and the square , the second consists of the two triangles and the rectangle . The area of the square must therefore be equal to the area of the rectangle, so .
Shear proof
If you shear a rectangle to form a parallelogram , the area is retained. This also allows the theorem to be proven. The animation illustrates the evidence:
With the help of the congruence theorems for triangles one still has to prove that the new height actually corresponds to the hypotenuse segment. This is not done here.
Shear proof of the cathetus set
The shear proof of the Pythagorean theorem also proves the cathetus theorem.
Proof of the complete group of theorems about similar triangles
The aspect ratios of the similar triangles immediately provide the two sets of legs and the set of heights. The Pythagorean theorem then results directly from the addition of the two cathetus sentences.
literature
- AM Fraedrich: The Pythagorean group of sentences . BI Wissenschaftsverlag, Mannheim, 1995.
- Max Koecher , Aloys Krieg : level geometry. 3rd, revised and expanded edition. Springer, Berlin a. a. 2007, ISBN 978-3-540-49327-3 .
- Hans Schupp: Elementarge Geometry ( Uni pocket books 669 Mathematics ). Schöningh, Paderborn 1977, ISBN 3-506-99189-2 , pp. 114-118.
- Hartmut Wellstein, Peter Kirsche: Elementary Geometry. A task-oriented introduction. Vieweg + Teubner, Wiesbaden 2009, ISBN 978-3-8348-0856-1 , pp. 70-78 ( excerpt (Google) ).
- Euclid : elements . Book I - § 47, Book II - § 14, Book VI - § 8, Book VI - § 31 ( online copy ).
Web links
- Christian Nöth: Proof techniques on the Pythagorean sentence group . Website of the mathematics didactics of the University of Würzburg
- Evidence collection for the Pythagorean theorem on cut-the-knot (English)
- Eric W. Weisstein : Pythagorean theorem . In: MathWorld (English). (also contains various evidence)
- Java applet for the height and leg set
- Proof of the height theorem with the help of the ray theorem
- Pythagorean sentence group Interactive learning unit with animations, constructions, control questions and solutions