Theorem of rays
The theorem of rays (one also speaks of the first, second and third theorem of rays) or the theorem of four lines is one of the most important statements in elementary geometry . It deals with route conditions and makes it possible to calculate unknown route lengths for many geometric considerations.
In synthetic geometry , the first two ray theorems can be generalized to affine translation planes with restrictions and apply without restrictions to Desargue planes . In contrast, the third beam set that in synthetic geometry applies three-beam set is called, generally only pappussche levels , → see Affine translational level # Strahlensatz and stretching .
Formulation of the theorems of rays
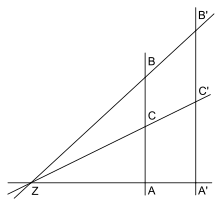
If two or three straight lines running through a point ( vertex ) are intersected by two parallels that do not go through the vertex, then the following statements apply:
- Two sections on one straight line relate to one another in the same way as the corresponding sections on the other straight line, for example or .
- The sections on the parallels behave like the corresponding sections measured from the apex on the same straight line, e.g. B. or .
- There are two sections on the parallels that correspond to each other, in the same relationship to each other, z. B. or . In contrast to the first two sets of rays, this theorem of rays requires at least three straight lines.
The first ray theorem thus relates to the proportions of ray sections, the second to the proportions of ray and parallel sections and the third to the proportions of parallel sections.
Remark (inversion of the ray law):
- If property 1 is fulfilled, one can infer parallel straight lines. If, on the other hand, property 2 is given, a corresponding conclusion that parallelism is not possible.
The name ray theorem is explained by the fact that one often only considers the special case in which the two parallels lie on the same side of the vertex ("V-figure"). Because then you do not need two straight lines intersecting at a vertex, but only two rays with a common origin.
Related geometric concepts
The theorem of rays is closely related to the concept of geometric similarity . The triangles and are in each of the three sketches, as well , and similarly in the diagram according to sentence 3 (in "formulation of the beams sets") to each other. This means in particular that the corresponding aspect ratios in these triangles coincide - a statement from which the theorem of rays results directly.
- See also: Similarity Theorems
Another concept related to the theorem of rays is that of centric stretching (a special geometrical mapping ). In the three sketches mentioned, the left one depicts the centric stretching with the center and stretching factor (mapping factor), for example, the points and onto the points or . The same applies to the central sketch; here the stretching factor is the same
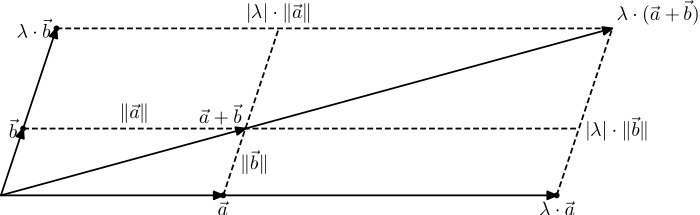
There is a similarly close relationship with vector calculus . The calculation rule
for two vectors and a real scalar is just another way of expressing the ray theorem, because it then applies:
- .
Here is the length ( Euclidean norm ) of the vector
Applications
measurement
In the relation equation of the ray theorem, three (known) quantities determine the (possibly unknown) fourth quantity. This can be used in the measurement of inaccessible, not directly measurable distances by choosing the not directly measurable distance as the (unknown) fourth variable in a ray set configuration. Simple measuring devices based on this principle are the Jacob's staff and the forester's triangle . The jump of the thumb to estimate distances is also based on this principle.
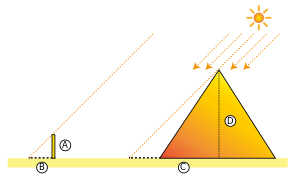
Height of the Great Pyramid
A simple example for the application of the theorem of rays should go back to the ancient Greek philosopher and mathematician Thales of Miletus . With the help of a stick, he determined the height of the Egyptian Great Pyramid by measuring the length of the shadow . In other languages, the ray theorem is therefore often referred to as the Thales theorem.
The following example calculation determines the height of the Great Pyramid with the help of the second theorem of rays, but it probably does not correspond to the exact calculation of the valley itself:
- First you determine the side length of the pyramid and then the length of the shadow of the same. Then you stick a stick vertically in the ground and measure its height and shadow length. The following values are then obtained:
- Height of the rod:
- Shadow length of the rod:
- Directly measurable shadow length of the pyramid:
- Side length of the pyramid:
- Total shadow length of the pyramid:
- Desired height of the pyramid:
- With the help of the ray theorem (sketch 2) the following equation is set up:
- The length of the side of the triangle is made up of half the side length and the length of the shadow of the pyramid. Converted to D you get:
River width
The theorem of rays can also be used in land surveying to determine the length of difficult-to-access stretches, such as the distance to opposite banks of bodies of water. The width of a river (see graphic on the right) can be determined as follows. First mark the end points A and B of the line to be determined, then construct an AC at right angles to AB. Such a construction can be carried out, for example, with the aid of a turnstile, corner mirror or double pentagon prism . On AC you choose an (arbitrary) point E from which you aim for point B on the other bank and then extend the distance EB beyond E in the opposite direction. Then at point C you construct a line at right angles to AC, which intersects the extension of EB at point D. Since the stretches AE, CE and CD are all on the same bank, they can be easily measured and the second set of rays then provides the river width you are looking for:
Division of a route
The first theorem of rays makes it possible to divide a segment in an (integer) ratio ( ) with a simple method - without calculations or measurements . At a given distance AB to draw a beam with a starting point in A a. Then, starting at A m + n , one cuts off successive stretches of equal length on the beam . The end point of the m + n th line is connected to B and then the parallel to this line is drawn through the end point of the m th line. This parallel divides the segment AB in the desired ratio .
proof
The route relationships set out in sentence 1 can be derived for triangles of equal area in the line theorem figure. Sentences 2 and 3 as well as the reverse of sentence 1 then result from the application of sentence 1 or the sentences that have already been proven.
Sentence 1
The perpendiculars from A 'and B' to the straight line have the same length, because it is parallel to . These perpendiculars are heights of the triangles ABB 'and ABA', which have the associated base side in common. For the areas, therefore, applies and further or area-united .
So then also applies:
- and
Applying the standard formula for calculating the area of triangles ( ) then yields
- and
Shorten supplies and .
If you dissolve both and set the right sides equal, the result is
or transformed for the route conditions on one beam each:
- .
Theorem 1 - Archimedes' proof
Apart from the proof given above, which goes back to a representation from Euclid's elements, shorter and more elegant proofs were possible in ancient Greece. It is enough to show the equality for one case of the possible relationships. The others follow immediately. Euclid himself only proves one case.
Here the proof is not quoted, but simply carried out according to Archimedes methodology:
With the usual side and angle designations for the triangles ABZ and A'B'Z according to the sketch above (for the formulation of the ray theorems ) it is shown that a: a '= b: b' applies. The angles and 'as well as and ' are the same as step angles . Denote the heights, which are given by the perpendicular from Z to the straight line, with h and h 'and their base points with H and H'. Since equal to 'the' remote 'cathetus and the hypotenuse is the same in the two right-angled triangles and AHZ A'H'Z relationship. (In 'modern' formulation: same opposite side from to hypotenuse)
So h: b = h ': b' and therefore h: h '= b: b'.
From the same 'is followed by appropriate consideration of the triangles and HBZ H'B'Z h the equation: a = h': A 'and h: h' = a: a '. And finally a: a '= b: b'. Which was to be proved.
Sentence 2
Construct an additional parallel to through A. This parallel intersects in G. Thus, according to construction and because of Theorem 1, the following also applies to the rays through A '
- which can be replaced by:
Sentence 3
Based on sentence 2:
So one has or switched too .
Reversal of sentence 1
Suppose and would not be parallel. Then there is a parallel to that goes through the point and intersects the ray in (*). Since the assumption applies, it results
On the other hand, it is also true after the first ray law
- .
This means that and both lie on the beam and are equidistant from . With that, however, the two points are identical, that is . This is a contradiction to the fact that the condition (*) should be about 2 different points. So the assumption of non-parallelism leads to a contradiction and therefore cannot be correct; Or to put it another way: It must apply.
Further applications and generalizations
- In ray optics, the ray sets describe the magnification ratios for a pinhole camera and - together with the lens equation - for a flawless thin lens .
- The statements of the first and second theorem of rays can be generalized in synthetic geometry to certain non-Desargue planes , the affine translation planes.
- The construction of a decimal number , as a practical application example of the third theorem in combination with number lines
literature
- Wendelin Degen, Lothar Profke: Fundamentals of affine and Euclidean geometry. Teubner, Stuttgart 1976, ISBN 3-519-02751-8 .
- Hans Schupp: Elementary Geometry. Schöningh, Paderborn 1977, ISBN 3-506-99189-2 , p. 124 ff. ( Uni-Taschenbücher 669 Mathematik ).
- Manfred Leppig (Ed.): Learning levels in mathematics. 1st edition, 4th printing. Girardet, Essen 1981, ISBN 3-7736-2005-5 , pp. 157-170.
- Hartmut Wellstein, Peter Kirsche: Elementary Geometry. A task-oriented introduction. Vieweg + Teubner Verlag 2009, ISBN 978-3-8348-0856-1 , pp. 36-41
Web links
- Symmetry and Similarity, Ray Theorems - Sinus Materials for the Ray Theorem (pdf)
- Alexander Bogomolny: Thales 'theorems and especially Thales' theorem on cut-the-knot.org
Individual evidence
- ↑ Not to be confused with the special case of the circular angle theorem, known in the German-speaking area as the Thales ' sentence .
- ↑ No works by Thales himself have survived. However, there are several historical sources that mention Thales' calculation of the pyramid height. However, all these sources were written several centuries after Thales's death and are slightly different in their description, so that in the end it cannot be said with certainty to what extent Thales knew the ray theorem itself or a special case of it as a geometric theorem or whether he was merely a physical one Applied observation. Sun is in Diogenes Laertius : " Jerome says that Thales even managed the height of pyramids to determine, by measured the shadow of the pyramid at the very moment in which his own shadow length corresponded to its body size. " Similar wording is carried out at Pliny : " Thales discovered how to determine the height of pyramids and other objects, namely by measuring the shadow of the object exactly at the point in time at which height and shadow are the same length. " In Plutarch, however, there is a description that may a knowledge of the theorem of rays suggests: " ... without difficulty and with the help of an instrument, he simply set up a stick at the end of the pyramid shadow and received two triangles created by the sun's rays ... then he showed that the height of the stick and the height of the pyramid are in the same ratio as the shadow length of the stick and the shadow length of the pyramid "(source: Biographie de s Thales in MacTutor )
- ^ Johann Friedrich Lorenz : Euclid's elements, fifteen books . Ed .: In the publishing house of the bookstore des Waysenhauses. Hall 1781, S. 87 ff . ( Euclid's Elements Sixth Book, The 2nd Movement. [Accessed October 29, 2016]).
- ↑ 6th book, L.2 engl.
- ^ Archimedes works. Translated and annotated by Arthur Czwalina Wiss. Buchgesellschaft, Darmstadt 1983, ISBN 3-534-02029-4











































![[FROM]](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e80b9404482bdbe7fe18d8435b3dd42fd39bb0)




































