Thales theorem

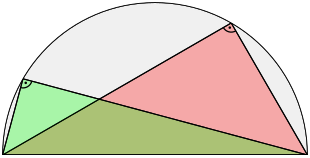
The theorem of Thales is a set of geometry and a special case of circle angle set . In simple terms it reads: All angles on the semicircular arc are right angles .

The first proof is attributed to the ancient Greek mathematician and philosopher Thales of Miletus . The statement of the sentence was already known in Egypt and Babylonia .

Formulation of the sentence and its reversal

Semicircle with right triangles

Exact formulation: If you construct a triangle from the two end points of the diameter of a semicircle ( Thales circle ) and another point of this semicircle, you always get a right-angled triangle .

Or: If the point C of a triangle ABC lies on a semicircle above the segment AB, then the triangle at C always has a right angle.

The reverse of the sentence is also correct: the center of the circumference of a right triangle is always in the middle of the hypotenuse , i.e. the longest side of the triangle that is opposite the right angle.

Or: If the triangle ABC has a right angle at C, then C lies on a circle with the hypotenuse AB as the diameter.

proofs

Euclid derives the sentence of Thales in the third volume of his elements with the help of the following sentences, which are also ascribed to Thales and are contained in the first volume:

• In any isosceles triangle, the angles at the base are the same.
• The inside angle sum in the triangle is 180 °.

Semicircle with triangle and center M

Let ABC be a triangle within a circle with [AB] as the circle diameter and the radius r . Then the center M of the segment [AB] is also the center of the circle. The route lengths [AM], [BM] and [CM] are therefore equal to the radius r .

The segment [CM] divides the triangle ABC into two triangles AMC and BCM, which are isosceles. The base angles of these triangles, i.e. the angles on the base side [AC] and [BC], are therefore always the same ( or in the figure). ${\displaystyle \alpha }$ ${\displaystyle \beta }$

The sum of the angles in the triangle ABC is 180 °:

${\displaystyle \alpha +\beta +\alpha +\beta \,=\,180^{\circ }}$

${\displaystyle 2(\alpha +\beta )\,=\,180^{\circ }}$

If you divide this equation by 2 on both sides, you get

${\displaystyle \alpha +\beta \,=\,90^{\circ }}$.

This shows that the angle     with vertex C is a right angle. ${\displaystyle \alpha +\beta }$

The reverse of Thales' theorem can be traced back to the statement that the diagonals of a rectangle are of equal length and bisect each other.

Another proof can be found here: Wikibooks: Evidence Archive .

Applications

Construction of a circular tangent

An important application of Thales' theorem is, among other things, the construction of the two tangents to a circle k through a point P outside of this circle.

Construction of the circle tangents

Given the radius r of the circle k with its center O and the distance between the point P and O. We only know that the point T must lie on the circular line, somewhere in the first quarter of the circle k. If one only took this condition into account, one could draw an infinite number of triangles OPT.

Since the upper tangent t running through P touches the circle k exactly at point T, the triangle OPT must have a right angle at point T ( basic property of the circle tangent ), or in other words: the line [OT] must be perpendicular to the tangent t .

To find a triangle OPT that is also right-angled, we determine the center H of the line [OP] using the perpendicular , draw a circle with the radius [HO] around the center H and use the principle of the Thales circle: All Triangles with the base side [OP], the third corner point of which lies on the Thales circle, are right-angled. Of course, this also applies to the triangle OPT.

The point of contact T can therefore only be the intersection of the circle k with the light gray circle. By connecting P with T one now obtains the desired tangent t (red in the drawing).

There is a second, symmetrical solution in the lower half of the circle. The tangent t '(also drawn in red) also touches the circle, namely at point T'.

Quadrature the rectangle

Another application is to square the rectangle .

Construction of real square roots

With the help of Thales's theorem, the following square roots can be constructed:

• ${\displaystyle {\sqrt {q}}}$off and off (see number greater than 1 ). ${\displaystyle q>0}$ ${\displaystyle {\sqrt {c}}}$ ${\displaystyle c>1}$
• ${\displaystyle {\sqrt {p\cdot q}}}$off off and off (see number less than 1 ). ${\displaystyle c=1,\;{\sqrt {q}}}$ ${\displaystyle q<1}$ ${\displaystyle {\sqrt {p}}}$ ${\displaystyle p<1}$

Number greater than 1

Number greater than 1: Construction by and with compasses and ruler ${\displaystyle {\sqrt {q}}}$ ${\displaystyle {\sqrt {c}}}$

If the square root of a number that is greater than is to be found without first dividing the number into - and - parts, the method shown in the adjacent picture is suitable. In principle , square roots of numbers that are smaller than are imaginable. ${\displaystyle 1}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle 1}$

It begins with the drawing of the route with length on a straight line not specified here . If the given number is a whole number , the product from the point is plotted on the straight line; ie is z. B. the number , the distance is plotted eight times. The resulting intersection brings the hypotenuse of the resulting triangle ${\displaystyle {\overline {BD}}}$ ${\displaystyle 1\;(=p)}$ ${\displaystyle q}$ ${\displaystyle q\cdot {\overline {BD}}}$ ${\displaystyle D}$ ${\displaystyle q=8}$ ${\displaystyle {\overline {BD}}}$ ${\displaystyle A}$ ${\displaystyle c=p+q}$ ${\displaystyle ABC.}$

Is a decimal number (eg. B. ), etc. is also possible using the third beam set to construct . ${\displaystyle q}$ ${\displaystyle 8{,}6}$ ${\displaystyle q}$

This is followed by the vertical line in the point and the halving of the side in Finally the Thales circle is drawn around . ${\displaystyle c}$ ${\displaystyle D}$ ${\displaystyle c}$ ${\displaystyle M.}$ ${\displaystyle M}$

• According to Euclid's theorem of heights , it follows ${\displaystyle h^{2}=p\cdot q,}$ ${\displaystyle h^{2}=1\cdot q,}$

thus the height of the right triangle is equal to the square root of ${\displaystyle ABC}$ ${\displaystyle q.}$

• According to the Euclidean theorem , it follows that ${\displaystyle a^{2}=p\cdot c,}$ ${\displaystyle a^{2}=1\cdot c,}$

thus the side length of the right triangle is equal to the square root of . ${\displaystyle a}$ ${\displaystyle ABC}$ ${\displaystyle c}$

Number less than 1

Number less than 1: Construction by and with compasses and ruler ${\displaystyle {\sqrt {p\cdot q}},\;{\sqrt {q}}}$ ${\displaystyle {\sqrt {p}}}$

If the square root of a number that is smaller than is sought, the method shown in the adjacent picture is suitable. ${\displaystyle 1}$

It starts from the point (value ) with a half-line . The route with length and the route with length are then determined. The result is the hypotenuse of the resulting triangle. If the given decimal number has only one decimal place , the product is plotted from the point ; ie is z. B. the route is removed eight times. The resulting intersection brings ${\displaystyle A}$ ${\displaystyle 0}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle 1}$ ${\displaystyle {\overline {AE}}}$ ${\displaystyle 0{,}1}$ ${\displaystyle c}$ ${\displaystyle ABC.}$ ${\displaystyle q}$ ${\displaystyle q\cdot {\overline {AE}}}$ ${\displaystyle A}$ ${\displaystyle q=0{,}8}$ ${\displaystyle {\overline {AE}}}$ ${\displaystyle D}$ ${\displaystyle c=p+q.}$

If the given decimal number has more than one place after the decimal point (e.g. ), it is possible, as already indicated above in number greater than 1 , to construct with the aid of the third theorem of rays. ${\displaystyle q}$ ${\displaystyle q=0{,}86}$ ${\displaystyle q}$

This is followed by the vertical line on the line in the point and the halving of the side in Finally the Thales circle (radius ) is drawn around . ${\displaystyle {\overline {AB}}}$ ${\displaystyle D}$ ${\displaystyle c}$ ${\displaystyle M.}$ ${\displaystyle =0{,}5}$ ${\displaystyle M}$

• According to Euclid's theorem of heights, ${\displaystyle h^{2}=p\cdot q,}$

thus the height of the right triangle is equal to the square root of ${\displaystyle h}$ ${\displaystyle ABC}$ ${\displaystyle p\cdot q.}$

Because of : ${\displaystyle h={\sqrt {p\cdot q}}}$

In the right triangle , the length is the geometric mean of the lengths and ${\displaystyle ABC}$ ${\displaystyle h}$ ${\displaystyle p}$ ${\displaystyle q.}$

• According to the Pythagorean theorem ,

for the side length ${\displaystyle b:}$

${\displaystyle b^{2}=q^{2}+p\cdot q,\;\;}$is in it , so it results ${\displaystyle p=1-q}$

${\displaystyle b^{2}=q^{2}+q\cdot \left(1-q\right)}$

${\displaystyle b^{2}=q^{2}+q-q^{2}\Rightarrow }$

${\displaystyle b={\sqrt {q}},}$

thus the side length of the right triangle is equal to the square root of ${\displaystyle b}$ ${\displaystyle ABC}$ ${\displaystyle q.}$

For the side length ${\displaystyle a:}$

With the corresponding values ​​for the side length, the result is analogous to the side length ${\displaystyle a}$ ${\displaystyle b:}$

${\displaystyle a={\sqrt {p}},}$

thus the side length of the right triangle is equal to the square root of ${\displaystyle a}$ ${\displaystyle ABC}$ ${\displaystyle p.}$

literature

• Max Koecher , Aloys Krieg : level geometry. 3rd, revised and expanded edition. Springer, Berlin a. a. 2007, ISBN 978-3-540-49327-3 .
• Hans Schupp: Elementarge Geometry (= Uni-Taschenbücher 669). Schöningh, Paderborn 1977, ISBN 3-506-99189-2 , p. 41.

Web links

Commons : Set des Thales  - collection of images, videos and audio files

• Euclid's proof (Theorem III.31), German by Rudolf Haller
• Animated, interactive graphics for understanding, Walter Fendt

Individual evidence

1. ↑ Diogenes Laertius : Lives and opinions of famous philosophers. First volume, book I − VI; Verlag von Felix Meiner, Leipzig 1921, p. 12, item 24 , accessed on April 18, 2017 . 
2. ^ Thomas Heath : A History of Greek Mathematics. Volume 1: From Thales to Euclid. Dover Publications, New York 1981, ISBN 0-486-24073-8 .
3. ^ Proclus . In: Euclid: The Elements. I, 250.20