A right triangle is a triangle with a right angle .
Designations
The longest side of a right triangle is called a hypotenuse . It is opposite the right angle .
Each of the two shorter sides in a right-angled triangle is called a cathete (from the Greek káthetos , the lowered, plumb line). So the cathets are the two sides of the right triangle that form the right angle . With respect to one of the two acute angle (in the sketch ) of the triangle, a distinction is adjacent leg of this angle (the angle the accompanying cathetus) and the opposite side (the opposite to the angle cathetus).

sentences
- The relationship between the lengths of the cathetus and the hypotenuse is described by the Pythagorean theorem , also known as the hypotenuse. (The sentence reads: If and are the lengths of the sides of the legs of a right triangle and the length of the sides of the hypotenuse, then the equation applies ). The Pythagorean theorem is a special case of the cosine law . The cosine of is 0, which significantly simplifies the formula.





- In other words, the Pythagorean theorem says that the sum of the areas of the two squares above the cathetus is equal to the area of the square above the hypotenuse . From this fact the cathetus theorem and the height theorem follow (see also Pythagoras group of sentences ). The height of a rectangular triangle the hypotenuse divides into two parts and so that the two sub-triangles with sides , , and , , in turn, are perpendicular. With knowledge of two of the six data ( , , , , and ) can be the missing four other values from those listed in the table below formulas to calculate.















|
Pythagorean theorem
|

|

|
|
Catheter set
|

|

|
|
Altitude rate
|

|
Calculation and construction

Construction SWW case, given are hypotenuse and angle

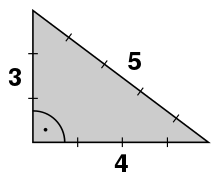
SSS case: smallest triple:

A right triangle is completely determined by three defining pieces: the right angle, a side, and another side or angle.
- If both sides are present, the triangle can be treated according to the SWS case .
- Arrange the cathetus perpendicular to the cathetus . The distance gives the missing hypotenuse and thus the triangle .





- If a cathetus and hypotenuse are present, the SSW case is used.
- Halve the hypotenuse and draw the Thales circle over the center . Is z. B. given the cathetus , the arc cuts the radius around the Thales circle in . The connection with completes the triangle .








- If there is one side and a non-right angle, the third angle can be determined using the angle sum. Then you can treat the triangle according to the WSW or SWW case .
- Is z. B. given the cathetus and the angle (WSW case), a straight line is drawn that forms the angle with the cathetus . The final vertical up down cuts the straight line in and thus creates the triangle .









- Is z. B. As can be seen in the adjacent picture, given the hypotenuse and the angle (SWW case), halve and draw the Thales circle over the center . When setting the angle with apex, the result is the Thales circle and thus the cathetus . The connection with supplies the cathetus and thus completes the right-angled triangle .












- If, in the SSS case, the two sides are in the same ratio as a Pythagorean triple , for example , the triangle is right-angled.

In the right triangle , the heights and are equal to the cathetus or .




| Mathematical formulas for the right triangle
|
|
Area
|

|
|

|
|
hypotenuse
|

|

|
|
Cathete
|

|

|

|

|
|
scope
|

|
|
height
|

|

|
|
angle
|

|

|

|
|
Inscribed radius
|

|
|
Perimeter radius
|

|
Inequalities
For the short sides and applies , therefore . Adding results to , so . According to the Pythagorean theorem , it follows from this and the inequalities








The right inequality is a special case of the inequality of the arithmetic and geometric mean .
Division of by the left inequality gives . Because of this it follows




From follows from , , for the reciprocals so . Multiplying by on both sides gives . Because of this, the more precise inequalities follow









The equations and apply if and only if , i.e. for a right-angled and isosceles triangle with the interior angles , and .






Excellent points
As can be seen from the picture, of the four "classic" marked points in the right-angled triangle, the height intersection (light brown) lies directly in the vertex of the right angle, corner point , and the center of the circumference (light green) in the middle of the triangle side, the center of gravity (dark blue) and the inscribed center (red) are inside the triangle.






The center of the Feuerbach circle (both light blue) is in the middle of the line and also within the triangle. On the Feuerbach circle there are nine excellent points , of which, however, only five can be seen due to the position of the height intersection . These are the side centers and as well as the height base points and two of the three centers of the so-called upper height sections , namely and lie on the side centers or The corresponding third center point is on the vertex Finally, the third height base point is found on the height intersection














The designations of the marked points and their positions are comparable to those of the acute-angled triangle .
The points , , and are, as with all triangles on the Euler straight (red).





Eddy's sentence
The sentence was only formulated in 1991, " but it is certainly much older ".

Fig. 2: Proof by means of the circular angle theorem
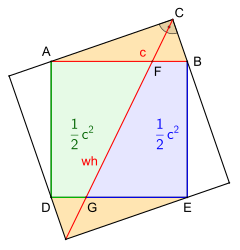
Fig. 1: Proof by symmetry
Let there be any triangle with the hypotenuse the hypotenuse square and with the bisector of the right angle at the vertex. The bisector cuts the hypotenuse square into two quadrilaterals and at the point and at the point










proofs
A) Proof by symmetry, Figure 1, both the geometric proof by supplementing it for the Pythagorean theorem .
B) Approach for an alternative proof, Figure 2:
- The two triangles and must be congruent.


- This only applies if the bisector runs through the center of the hypotenuse square .


First the center point of the hypotenuse is determined, then the circle with the radius um is drawn in and the mid-perpendicular of the diameter with the intersection points and are entered. The point of intersection corresponds to the center of the hypotenuse square. Finally, connect the point with .













The inscribed triangle has the central angle with the angular width equal to the apex . According to the theorem of angles (central angle theorem) , the angle consequently has the angular width so that the bisector also runs through the center of the hypotenuse square







This confirms that the two triangles and are congruent, so the quadrilaterals and have the same area.




See also
Web links
Notes and individual references
-
↑ The term “hypotenuse” comes from the synonymous, ancient Greek term ὑποτείνουσα, hypoteinousa , which is derived from: hypo - under and teinein - tension, extend.
-
↑ Arne Madincea: The Feuerbach Circle… The sentence about the 9-point circle: Exercise 1, p. 2 ff. (PDF) In: Materials for mathematics lessons. Herder-Gymnasium Berlin, p. 7 , accessed on November 25, 2018 .
-
↑ a b Wolfgang Zeuge: Useful and beautiful geometry: A slightly different introduction to Euclidean geometry . Springer Spectrum, Wiesbaden 2018, ISBN 978-3-658-22832-3 , 2.7 Eddy's theorem, p. 30 ( limited preview in Google Book Search [accessed August 16, 2019]).
-
^ Jörg Meyer: Symmetry. 3. Symmetry in problem solving. Saarland University, Department of Mathematics, p. 4 , accessed on August 15, 2019 .














































































































