Height intersection

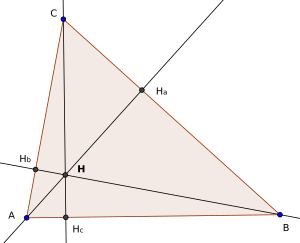
The height intersection (also: orthocenter ) of a triangle is the intersection of its three heights , i.e. H. the perpendicular to the sides of the triangle through the opposite corners. The intersection point is one of the four classic excellent points of the triangle.

In the sketch the heights are marked with [ AH _a ], [ BH _b ] and [ CH _c ]. If the given triangle ABC is acute-angled , the height intersection point H is located within the triangle. If, on the other hand, the triangle has an obtuse angle (i.e. an angle greater than 90 °), H is outside. Finally, in the right-angled case, H corresponds to the vertex of the right angle .

proof

Triangle with heights and parallels to the sides

To prove that all three heights of the triangle intersect at one point, draw the parallels to the sides of the triangle through the opposite corners, so that a larger triangle is created. Two of the four partial triangles of the new triangle form a parallelogram . In a parallelogram, opposite sides are the same length. Therefore, the sides of the new triangle are twice as long as the corresponding sides of the original triangle. The heights of the original triangle therefore coincide with the perpendiculars (line symmetry) of the new triangle. Since the perpendiculars of a triangle intersect at a point (→ see circumference ), this must also apply to the heights of the starting triangle . ${\ displaystyle ABC}$ ${\ displaystyle A'B'C '}$

Conversely, the triangle can be inscribed in the triangle as the triangle of its central parallels. This means that the center of the circumference of the original triangle coincides with the vertical intersection of the inscribed triangle. ${\ displaystyle A'B'C '}$ ${\ displaystyle ABC}$

Generalization in synthetic geometry

The mitbewiesene in the proof equivalency of the height of intersection-set for agents solders set , can be in the synthetic geometry of affine translation planes with an orthogonality generalize if each route the plane has a center, that is, if the level of the affine Fano axiom met. Then it can be concluded from the existence of these intersection points for any triangles that the translation plane is a Pappus plane . In this respect, the height intersection theorem is treated as an axiom in synthetic affine geometry.

properties

The triangle consisting of the base points H _a , H _b and H _{c of} the heights is called the height base triangle of the triangle ABC . If the triangle ABC is acute-angled, then the vertical intersection point H of the triangle ABC is the inscribed center of the height base triangle; if the triangle ABC is obtuse-angled, then the height intersection point H of the triangle ABC is a circle center of the height base point triangle.

The products of the height sections are the same:

{\ displaystyle {\ overline {AH}} \ cdot {\ overline {HH_ {a}}} = {\ overline {BH}} \ cdot {\ overline {HH_ {b}}} = {\ overline {CH}} \ cdot {\ overline {HH_ {c}}}}

.

The intersection point - like the center of gravity and the center of the circumference - lies on Euler's straight line .

The base points of the heights and the midpoints of the "upper height sections" (each between the height intersection and a corner) lie on the Feuerbach circle .

If the height intersection is reflected on the three sides of the triangle, the image points lie on the circumference.

Coordinates

Vertical intersection of a triangle (orthocenter, ) ${\ displaystyle X_ {4}}$
Trilinear coordinates	${\ displaystyle \ sec \ alpha \,: \, \ sec \ beta \,: \, \ sec \ gamma}$
Barycentric coordinates	${\ displaystyle \ tan \ alpha \,: \, \ tan \ beta \,: \, \ tan \ gamma}$

literature

H. Schupp: Elementary Geometry . UTB Schöningh 1977, ISBN 3-506-99189-2 , p. 50.
Wendelin Degen and Lothar Profke: Fundamentals of affine and Euclidean geometry , Teubner, Stuttgart, 1976, ISBN 3-519-02751-8
Max Koecher , Aloys Krieg : level geometry, 3rd edition, Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3

Web links

http://www.mathe-werkstatt.de/titel.htm interactive Java applet that shows the curve of the height intersections