Right angle
A right angle , also right for short , is an angle of 90 ° and thus the fourth part of a full angle to 360 °. Two lines or lines that intersect or touch at a right angle are called right-angled , perpendicular, or orthogonal . Right angles appear in many geometric figures and constructions and are indicated in drawings by a small quarter circle with a point or a small square . The right angle was at times a legal unit alongside the full angle in Germany and Switzerland.
definition
Both Euclid in his work The Elements (approx. 300 BC) and David Hilbert in his system of axioms of Euclidean geometry (1899) define a right angle as an angle that is congruent to its secondary angle :
"If a straight line, placed on a straight line, forms the same secondary angles, then each of the same secondary angles is right"
The adjective "right" does not mean right , but right in the sense of upright ( Latin rectus ). Alternatively, since the 16th century at the latest, a right angle has also been defined as an angle to which a quarter circle belongs. Both definitions are equivalent to each other, because two secondary angles together result in a straight angle , which corresponds to a semicircle .
Examples
In the plane, for example, form a right angle:
- the coordinate axes of a Cartesian coordinate system
- two adjacent sides of a rectangle
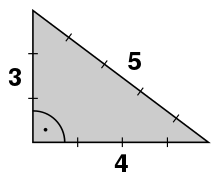
- the two legs of a right triangle
- the two diagonals of a dragon square
- the two semi-axes of an ellipse
- the connecting lines of a point on a semicircle with the endpoints of the diameter ( Thales theorem )
In space, for example, form a right angle:
- two of the coordinate axes of a three-dimensional Cartesian coordinate system
- two neighboring edges of a cuboid
- two of the three space diagonals of an octahedron
- two mutually orthogonal vectors
- the perpendicular on a plane with every straight line of the plane through the perpendicular base
In an orthogonal polygon or an orthogonal polyhedron , all of the adjacent edges form right angles.
Determination of right angles
Between routes
Two lines and , according to the Pythagorean theorem, form a right angle if and only if for the lengths of the lines
applies. The integer solutions of this equation are called Pythagorean triples . Two lines that meet at one point and whose lengths or units are exactly then form a right angle with one another if the connecting line of the two end points is units long, because
- . The harpedo tapes (rope tensioners) in ancient Egypt used this to construct the right angle.
Between function graphs
The graphs of two linear functions and intersect at a right angle if and only if for the product of the slopes
applies. For example, the graphs of the two linear functions and intersect at right angles, because
- .
More generally, the graphs of two differentiable functions intersect and at a right angle if and only if at the intersection the product of the derivatives (of the tangent slopes )
results. For example, the graphs of the functions and intersect at right angles because and
- .
Between curves
Two intersecting straight lines form a right angle in a Cartesian coordinate system if and only if for the scalar product of the direction vectors and the two straight lines
applies. For example, there are two straight lines with the direction vectors and perpendicular to each other
is. More generally, two intersecting differentiable curves form a right angle with one another if the scalar product of their tangential vectors vanishes at the point of intersection.
trigonometry
The following applies to the trigonometric functions sine and cosine , tangent and cotangent as well as secant and cotangent of a right angle :
- and are not defined
units
A right angle corresponds in the various angular dimensions :
- 1 right = 90 ° = 90 degrees
- 1 right = / 2 radians in radians ( SI unit )
- 1 right = 100 g = 100 gon = 100 grads
- 1 right = 8 "= 8 nautical dash
- 1 right = 1600¯ = 1600 mil = 1600 artillery line
- 1 right = 6 h = 360 m = 21,600 s per hour
From July 5, 1970 to November 29, 1973, in addition to the full angle (360 degrees), the right angle with the symbol ∟ was a legal unit in Germany . Until December 31, 1996, the right angle was the legal entity in Switzerland.
Construction by drawing
Tools for drawing right-angled lines at school are, for example, a math paper or a set square . For construction with compasses and ruler, see Lot (mathematics) . When technical drawing on the drawing board one is drawing head with characters rails used. In the metal and woodworking trade, a square measure or a gauge is used to measure right angles .

|

|
|
|
Construction of a right angle at one point of a straight line with a compass and ruler
|
Construction of a right angle at a point ( freely selectable) of a half-line , with limited space, with the help of the Thales circle , animation
|
In practice, of course, you only get approximations to the geometric concept of the right angle.
Construction practical
Various mechanical aids have been developed over the years to construct right angles over longer distances. The simplest way to construct a right angle is to use a cord that is knotted into 12 equal parts ( 12-knot cord or calculating rope ). These are stretched to form a triangle with the lengths of the edges . The right angle (exactly 90 °) lies between the two short sides ( cathetus ). This method was used in architecture in ancient Egypt and in the Middle Ages . For example, if you can construct a horizontal line with a hose level , you can construct a vertical line. Or if you can construct a vertical line with the plumb line, you can construct such a horizontal line. The underlying principle is called the Pythagorean triple .
In the Roman civil engineering was in the Limitation one of settlements Groma for stakeout used right angle, in recent times this was a Oldham used. In geodesy , an angled prism or a theodolite is used for cadastral surveys with the orthogonal method .
Today, these devices have largely been replaced by electro-optical rangefinders , such as total stations .
Marking and coding
In German-speaking countries and a number of other European countries, a quarter circle connecting both legs of the angle with a point is used to identify right angles in drawings. Occasionally the point is omitted. In English-speaking countries, a second right angle connecting both legs of the angle and forming a small square (or parallelogram in the case of an oblique representation ) is drawn in for identification.
In the character set , right angles are defined and coded as follows:
| character | Unicode | Surname | HTML | |||
|---|---|---|---|---|---|---|
| position | designation | hexadecimal | decimal | named | ||
| ∟ | U + 221F | right angle | Right angle | & # x221F; | & # 8735; | - |
| ⦜ | U + 299C | right angle variant with square | Variant of a right angle with a square | & # x299C; | - | - |
| ⦝ | U + 299D | measured right angle with dot | Measured right angle with point | & # x299D; | - | - |
| ⊾ | U + 22BE | right angle with arc | Right angle with arch | & # x22BE; | & # 8894; | - |
The symbol ∟ for the right angle was first used by the Greek mathematician Pappos in the 4th century AD.
Historical
Right angles - like the circle , the straight line, etc. - are abstractions of the human mind in its permanent confrontation with nature and its own needs. They do not occur in animate nature and are also approximately extremely rare in inanimate, visible nature. Humans probably first realized the right angle in the art of braiding and weaving (e.g. in mats and fabrics ). Even with the recurring construction of huts, there were almost right angles between the horizontal ground and upright branches, as well as between vertical posts and horizontal mesh panels. This basic pattern, once found, was continuously refined and so the first stone monuments with right-angled corners and ornaments were created thousands of years later (see Göbekli Tepe ). Right-angled constructions are rather rare in the megalithic buildings of the Neolithic , but they play an important role in Stonehenge and in the dolmens of the Caucasus.
While Egyptians, Greeks, Romans and even the Mesoamerican cultures used the right angle in a variety of ways, it takes a backseat in individual phases of European architecture ( Gothic , Baroque ) or in individual modernist architects (e.g. Frank Gehry ).
Web links
- Eric W. Weisstein : Right Angle . In: MathWorld (English).
Individual evidence
- ↑ Clemens Thaer (ed.): The elements of Euclid (= Ostwald's classic of the exact sciences . Volume 235 ). Academic Publishing Company, Leipzig 1933.
- ↑ a b Johannes Tropfke : History of Elementary Mathematics . tape 4 : plane geometry . de Gruyter, Berlin 1940, ISBN 3-11-162150-2 , p. 66 (first edition: 1903, reprint).
- ↑ Hans-Joachim Schönknecht: Myth - Science - Philosophy: On the Origin of Occidental Rationality in Ancient Greece, Vol. 1-3 ; 2.4.1 From the practice of field measurement to mathematical geometry , Tectum Wissenschaftsverlag, 2017, p. 98 ff. ( Limited preview in the Google book search), accessed on May 14, 2020
- ↑ BGBl. 1970 I p. 981, 982 , BGBl. 1973 I p. 1761
- ↑ Florian Cajori: A History of Mathematical Notations . Volume 1. Cosimo, 2013, ISBN 1-60206-685-X , p. 401 .







![[AC]](https://wikimedia.org/api/rest_v1/media/math/render/svg/49b377aec839d74e0b48a42d2ba192d3efefc575)
![[BC]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)