Differentiability

Graph of a differentiable function

In mathematics, differentiability is the property of a function to be approximated locally around a point in a linear manner . The term differentiability is explained not only for real-valued functions on the set of real numbers , but also for functions of several variables, for complex functions, for mappings between real or complex vector spaces and for many other types of functions and mappings. For some types of functions (for example for functions of several variables) there are several different differentiability terms.

The question of differentiability belongs to the problems of differential calculus , a branch of analysis .

Real-valued functions of a real variable

Definitions

Black: Graph of the function f
Red: Graph of the linear function g, which approximates f near the point x ₀

To the 2nd definition of differentiability

Differentiable functions are precisely those functions that can be locally approximated by precisely one linear function.

In the simplest case, one considers a real-valued function of a real variable , i.e. a function whose function values ​​are real numbers and whose domain is an open interval of real numbers. Such a function is differentiable at a point from its domain if the derivation of exists at this point. There are essentially two equivalent definitions for the existence of the derivative: ${\displaystyle f\colon D\to \mathbb {R} }$ ${\displaystyle D\subset \mathbb {R} }$ ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle f}$

1. Definition

A function is then differentiable at the point of its domain of definition if the two-sided limit value of the difference quotient ${\displaystyle f}$ ${\displaystyle x_{0}}$

${\displaystyle \lim _{x\rightarrow x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{h\rightarrow 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}}$

exists. This limit is known as the derivative of at the point written . ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle f'(x_{0})}$

2. Definition

A function is differentiable at the point of its domain if and only if a real number (which may depend on) and a function (also dependent on) (error of approximation) exist with the following properties: ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle m}$ ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle r}$

1. ${\displaystyle f(x_{0}+h)=f(x_{0})+m\cdot h+r(h)}$
2. For goes faster than linear to 0, that is: ${\displaystyle h\to 0}$ ${\displaystyle r(h)}$

${\displaystyle {\tfrac {r(h)}{h}}\to 0}$ For ${\displaystyle h\to 0}$

The function can thus be near by a linear function with ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle g}$

${\displaystyle g(x_{0}+h)=f(x_{0})+m\cdot h}$

approximate except for the error . The value is called the derivative of at that point . ${\displaystyle r(h)}$ ${\displaystyle m}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$

Differentiable functions are therefore precisely those functions that can be approximated locally by linear functions (see figure).

Both definitions are equivalent: If it is differentiable according to the 1st definition, then one selects for the limit value from the definition and sets ${\displaystyle f}$ ${\displaystyle m}$

${\displaystyle r(h)=f(x_{0}+h)-f(x_{0})-m\cdot h.}$

Then the first quality is fulfilled by and , and the second because of ${\displaystyle m}$ ${\displaystyle r(h)}$

${\displaystyle {\begin{aligned}\lim _{h\to 0}{\frac {r(h)}{h}}&=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})-m\cdot h}{h}}\\&=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}-m=m-m=0.\end{aligned}}}$

Conversely, if the 2nd definition is fulfilled, the equation is obtained by transforming the first property

${\displaystyle {\frac {f(x_{0}+h)-f(x_{0})}{h}}=m+{\frac {r(h)}{h}}}$

and the limit of the difference quotient then exists because of

${\displaystyle \lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}=m+\lim _{h\to 0}{\frac {r(h)}{h}}=m+0=m.}$

A function is called differentiable (without restriction to a special point) if and only if it is differentiable at every point in its domain. The function is then called the derivative function or, for short, the derivative of . ${\displaystyle f'\colon x\mapsto f'(x)}$ ${\displaystyle f}$

Explanations

Graphically, the property differentiability can be interpreted in such a way that a function is differentiable at the point if exactly one tangent exists in the associated point of the graph of which is not perpendicular. The tangent is the graph of the linear function mentioned in the 2nd definition  . ${\displaystyle x_{0}}$ ${\displaystyle (x_{0},f(x_{0}))}$ ${\displaystyle f}$ ${\displaystyle g}$

The derivative of at the point is the slope of this tangent. The difference quotients mentioned in the first definition are the gradients of secants through the point and another point on the curve . The function can therefore be differentiated at the point when the slopes of these secants converge to the slope of the tangent at the limit crossing . ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle (x_{0},f(x_{0}))}$ ${\displaystyle (x,f(x))}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle x\to x_{0}}$

Differentiability follows continuity : every function that can be differentiated at one point is also continuous there. Every function that can be differentiated on its domain is continuous. The reverse is not true. The non-differentiable functions listed below are all continuous.

Examples of differentiable functions

From the derivation rules it follows:

• Every function that can be represented by a polynomial is differentiable.
• Sums, products and quotients of differentiable functions are differentiable.
• Concatenations of differentiable functions are differentiable.
• The inverse function of a bijective differentiable function is then differentiable exactly if is. ${\displaystyle f^{-1}}$ ${\displaystyle f}$ ${\displaystyle y_{0}=f(x_{0})}$ ${\displaystyle f^{\prime }(x_{0})\neq 0}$

From the limit theorems for power series it follows:

• Every function that can be represented locally by a power series is differentiable.

Examples of non-differentiable functions

The Heaviside function is not continuous at the point 0 and therefore not differentiable.

Since every differentiable function is continuous, every discontinuous function (for example a step function or the Dirichlet function ) is an example of a non-differentiable function. But there are also functions that are continuous, but not or not everywhere differentiable.

Root function

Root function graph

The root function , is at the point not differentiable. The difference quotient ${\displaystyle f\colon [0,\infty )\to \mathbb {R} }$ ${\displaystyle f(x)={\sqrt {x}}}$ ${\displaystyle x_{0}=0}$

${\displaystyle {\frac {{\sqrt {x}}-{\sqrt {0}}}{x-0}}={\frac {\sqrt {x}}{x}}={\frac {1}{\sqrt {x}}}}$

strives for towards infinity, so does not converge. The graph of the function has a tangent at this point, but this runs vertically and therefore has no slope. ${\displaystyle x\to 0}$ ${\displaystyle x_{0}}$

Amount function

Function graph and graph of the derivative of ${\displaystyle f(x)=|x|}$

The amount function can not be differentiated at this point . ${\displaystyle f(x)=|x|}$ ${\displaystyle 0}$

For is and with it ${\displaystyle x>0}$ ${\displaystyle f(x)=x}$

${\displaystyle \lim _{x\searrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\searrow 0}{\frac {x-0}{x-0}}=1}$.

For is against and consequently ${\displaystyle x<0}$ ${\displaystyle f(x)=-x}$

${\displaystyle \lim _{x\nearrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\nearrow 0}{\frac {-x-0}{x-0}}=-1}$.

Since the left-hand and right-hand limit values do not match, the limit value does not exist. The function cannot therefore be differentiated at the point under consideration. ${\displaystyle f}$

However, the right-hand derivative exists at this point ${\displaystyle 0}$

${\displaystyle f'_{+}(0)=\lim _{x\searrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\searrow 0}{\frac {x-0}{x-0}}=1}$

and the left-hand derivative

${\displaystyle f'_{-}(0)=\lim _{x\nearrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\nearrow 0}{\frac {-x-0}{x-0}}=-1}$.

The function graph has a kink at this point . There is, so to speak, a left-hand tangent with a gradient and a right- hand tangent with a gradient . For every slope between and there is a straight line that “touches” the function graph at the point , but does not “nestle”. ${\displaystyle 0}$ ${\displaystyle -1}$ ${\displaystyle +1}$ ${\displaystyle -1}$ ${\displaystyle +1}$ ${\displaystyle (0,0)}$

This is a typical behavior for functions defined in sections, where the function values ​​match at the interfaces, but not the derivatives. In contrast, the graphs of differentiable functions have no kinks.

A third example

Graph of the function with for and . ${\displaystyle f}$ ${\displaystyle f(x)=\vert x\vert \sin(1/x)}$ ${\displaystyle x\neq 0}$ ${\displaystyle f(0)=0}$

The function

${\displaystyle f(x)={\begin{cases}x\sin \left({\tfrac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}}}$

is continuous at the point 0, but not differentiable (but everywhere else). The following applies to the difference quotient at position 0

${\displaystyle {\frac {f(x)-f(0)}{x-0}}={\frac {x\sin \left({\tfrac {1}{x}}\right)-0}{x-0}}=\sin \left({\tfrac {1}{x}}\right).}$

The Limes for does not exist. There are also no one-sided limit values. Rather, when it approaches 0, the difference quotient oscillates infinitely often between the values ​​−1 and 1 and assumes every intermediate value infinitely often. ${\displaystyle x\to 0}$ ${\displaystyle x}$

Weierstrass function

Graph of a real Weierstrass function in the interval . It is continuous, but nowhere differentiable. ${\displaystyle [-2,2]}$

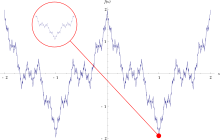
The Weierstrass function named after its discoverer

${\displaystyle f(x)=\sum _{k=1}^{\infty }{\frac {2^{k}\sin(2^{k}x)}{3^{k}}}}$

is constant everywhere, but nowhere differentiable.

Wiener trial

Path of a Viennese Trial

The mathematical Brownian motion provides further examples: Almost every path of a Wiener process is continuous as a function , but nowhere differentiable. ${\displaystyle X_{\cdot }(\omega )\colon \mathbb {R} \to \mathbb {R} ,\ t\mapsto X_{t}(\omega )}$

Constant differentiability and higher derivatives

Example of a function that is not continuously differentiable

The function with for and is differentiable, but not continuously differentiable ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ ${\displaystyle f(x)=x^{2}\sin \left({\tfrac {1}{x}}\right)}$ ${\displaystyle x\neq 0}$ ${\displaystyle f(0)=0}$

A function is called continuously differentiable if it is differentiable and its derivative is continuous . Even if a function is differentiable everywhere, the derivative does not have to be continuous. For example is the function

${\displaystyle f(x)={\begin{cases}x^{2}\cos \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}}}$

at every point, inclusive , differentiable because ${\displaystyle x=0}$

${\displaystyle f'(0)=\lim _{h\to 0}{\frac {h^{2}\cos \left({\tfrac {1}{h}}\right)-0}{h}}=0.}$

The derivation

${\displaystyle f'(x)={\begin{cases}2x\cos \left({\frac {1}{x}}\right)+\sin \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}}}$

but is not continuous at 0.

A function is said to be twice differentiable if its derivative function is differentiable. Correspondingly, three times, four times, ..., -times is defined differentiable . The higher derivatives are with , , ,, ... , respectively. ${\displaystyle f}$ ${\displaystyle f'}$ ${\displaystyle k}$ ${\displaystyle f''}$ ${\displaystyle f'''}$ ${\displaystyle f^{(4)}}$ ${\displaystyle f^{(k)}}$

Since continuity follows from the differentiability of a function, in the case of a twice differentiable function the function itself and the first derivative are automatically continuous. However, the second derivative need not be continuous. Accordingly, at a times differentiable function, the function itself and all derivatives , , ... to the th derivation continuous. However , this need not apply to the -th derivative . If this is also continuous, then -mal is called continuously differentiable. If all derivatives are differentiable again, the function is called infinitely differentiable or smooth . ${\displaystyle f}$ ${\displaystyle f'}$ ${\displaystyle f''}$ ${\displaystyle k}$ ${\displaystyle f'}$ ${\displaystyle f''}$ ${\displaystyle (k-1)}$ ${\displaystyle f^{(k-1)}}$ ${\displaystyle k}$ ${\displaystyle f^{(k)}}$ ${\displaystyle f}$ ${\displaystyle k}$

The set of all -time continuously differentiable functions with the definition set is called . The set of infinitely often differentiable functions is called . A -time continuously differentiable function is therefore also called a function of the differentiation class , in short: a function of the class or function. An infinitely often differentiable function is called a function of the (differentiation) class or function. ${\displaystyle k}$ ${\displaystyle D}$ ${\displaystyle C^{k}(D)}$ ${\displaystyle C^{\infty }(D)}$ ${\displaystyle k}$ ${\displaystyle C^{k}}$ ${\displaystyle C^{k}}$ ${\displaystyle C^{k}}$ ${\displaystyle C^{\infty }}$ ${\displaystyle C^{\infty }}$

The function

${\displaystyle f(x)=x\cdot |x|={\begin{cases}-x^{2}&x<0\\\ \ x^{2}&x\geq 0\end{cases}}}$

is differentiable, its derivative is the function that is continuous, but not differentiable at the point 0. The function is thus continuously differentiable, but not twice differentiable at position 0. The function is accordingly ${\displaystyle f'(x)=2\,|x|}$ ${\displaystyle f}$

${\displaystyle f(x)=x^{k-1}\cdot |x|={\begin{cases}-x^{k}&x<0\\\ \ x^{k}&x\geq 0\end{cases}}}$

${\displaystyle (k-1)}$-time continuously differentiable, but not -time differentiable at position 0 . ${\displaystyle k}$

Complex functions

→ Main article : Holomorphic function

For complex functions , i.e. complex-valued functions of a complex variable, differentiability is defined in the same way as real functions. Let it be an open subset of the complex plane and a point of this subset. A function is called complex differentiable in the point , if the limit value ${\displaystyle U\subset \mathbb {C} }$ ${\displaystyle z_{0}\in U}$ ${\displaystyle f\colon U\rightarrow \mathbb {C} }$ ${\displaystyle z_{0}}$

${\displaystyle \lim _{h\rightarrow 0}{\frac {f(z_{0}+h)-f(z_{0})}{h}}=\lim _{z\rightarrow z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}}$

exists. In this case, this limit is referred to as . ${\displaystyle f'(z_{0})}$

A function is called holomorphic in point , if a surrounding area of exists in is complex differentiable. Holomorphic functions are automatically infinitely often complex differentiable and even analytical . ${\displaystyle f}$ ${\displaystyle z_{0}}$ ${\displaystyle z_{0}}$ ${\displaystyle f}$

Real-valued functions of several variables

For functions of several variables, i.e. functions that are defined on open subsets of Euclidean space , there are several differently strong concepts of differentiability. The following is an open set. The elements of can be written as tuples . A function is also given. We consider a fixed point and consider differentiability in the point . ${\displaystyle U\subset \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle x=(x_{1},\dots ,x_{n})}$ ${\displaystyle f\colon U\to \mathbb {R} }$ ${\displaystyle a=(a_{1},\dots ,a_{n})\in U}$ ${\displaystyle a}$

Partial differentiability

→ Main article : Partial derivative

This is the weakest concept of differentiability. The function is called partially differentiable at the point in direction , if the partial derivative ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle x_{i}}$

${\displaystyle {\frac {\partial f}{\partial x_{i}}}(a)=\lim _{h\to 0}{\frac {f(a_{1},\dots ,a_{i-1},a_{i}+h,a_{i+1},\dots ,a_{n})-f(a)}{h}}}$

exists. So you consider all variables except for constant and consider the resulting function of a variable. ${\displaystyle x_{i}}$

The function is called partially differentiable if all partial derivatives exist at every point. It is called continuously partially differentiable if all partial derivatives are continuous functions of after . ${\displaystyle f}$ ${\displaystyle U\subset \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} }$

Partial differentiability does not result in continuity, but only continuity in the direction of the coordinate axes.

Directional derivative

→ Main article : Directional derivation

If a unit vector , then the (two-sided) directional derivative of in direction at the point is defined as ${\displaystyle v\in \mathbb {R} ^{n}}$ ${\displaystyle f}$ ${\displaystyle v}$ ${\displaystyle a}$

${\displaystyle D_{v}f(a)=\lim _{h\to 0}{\frac {f(a+hv)-f(a)}{h}}}$.

If one only looks at positive ones , one obtains the one-sided directional derivative ${\displaystyle h}$

${\displaystyle D_{v}^{+}f(a)=\lim _{h\searrow 0}{\frac {f(a+hv)-f(a)}{h}}}$.

The function is called (one-sided) differentiable in the direction of , if the (one-sided) directional derivative of in direction exists. The directional derivatives in the direction of the unit vectors of the standard basis are precisely the partial derivatives ${\displaystyle f}$ ${\displaystyle v}$ ${\displaystyle f}$ ${\displaystyle v}$

${\displaystyle {\frac {\partial f}{\partial x_{i}}}(a)=D_{e_{i}}f(a)}$.

Total differentiability

→ Main article : Total differentiability

The function is called totally differentiable at the point , if a linear mapping and a function exist, so that apart from the error it can be approximated by, ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle L\colon \mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle r}$ ${\displaystyle f}$ ${\displaystyle r}$ ${\displaystyle L}$

${\displaystyle f(a+v)=f(a)+Lv+r(v),}$

and goes from higher than first order to 0, that is for . ${\displaystyle r}$ ${\displaystyle {\tfrac {r(v)}{\|v\|}}\to 0}$ ${\displaystyle \|v\|\to 0}$

The linear mapping is called the total derivative of in the point . It is designated with . The matrix representation with reference to the standard basis is called Jacobi matrix and is also referred to as or . The function is called totally differentiable if it is totally differentiable in every point. ${\displaystyle L}$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle Df(a)}$ ${\displaystyle J_{f}(a)}$ ${\displaystyle Df(a)}$ ${\displaystyle f}$

A totally differentiable function is also continuous.

In the more recent mathematical literature one speaks mostly simply of differentiability instead of total differentiability. The total derivative is also called the differential.

Relationships between the different concepts of differentiability

• If it is bilaterally differentiable in every direction, it is especially partially differentiable. ${\displaystyle f}$ ${\displaystyle f}$
• If totally differentiable, then it is differentiable in every direction (i.e. especially also partially differentiable). The entries of the Jacobi matrix are the partial derivatives ${\displaystyle f}$ ${\displaystyle f}$

  ${\displaystyle J_{f}(a)=\left({\frac {\partial f}{\partial x_{1}}}(a)\quad \dots \quad {\frac {\partial f}{\partial x_{n}}}(a)\right)}$.

The directional derivative in direction is obtained by applying the total derivative (a linear map) to the vector . ${\displaystyle v=(v_{1},\dots ,v_{n})}$ ${\displaystyle v}$

${\displaystyle D_{v}f(a)=Df(a)\,v=\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}(a)\,v_{i}}$

The inversions do not apply:

• From the partial differentiability follows neither the total differentiability nor the bilateral or one-sided differentiability in directions that are not coordinate directions.
• Also from the two-sided differentiability in all directions does not follow total differentiability. Not even if the candidate for the total derivative, the mapping , is linear. ${\displaystyle v\in \mathbb {R} ^{n}\mapsto D_{v}f(a)}$

It is different if one assumes not only the existence but also the continuity of the partial derivatives.

• If continuously partially differentiable, then it is also totally differentiable. ${\displaystyle f}$ ${\displaystyle f}$

Therefore, one calls continuously partially differentiable functions simply continuously differentiable. Here, too, the reverse does not apply:

• The continuity of the partial derivatives does not follow from total differentiability.

Overall, the following applies:

continuous partial differentiability ⇒ total differentiability ⇒ differentiability in every direction ⇒ partial differentiability,

however, none of the converse is true.

Examples

• Every function that can be represented as a polynomial in the variables is continuously differentiable. ${\displaystyle x_{1},\dots ,x_{n}}$
• Sums, products, quotients and chains of continuously differentiable functions are continuously differentiable.

Counterexamples

All counterexamples are functions on the . The coordinates are designated with and instead of and . Of interest here is only the differentiability and continuity at the origin . Everywhere else, the functions are continuously differentiable. ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle (0,0)}$

Partially differentiable, but not continuous and not all directional derivatives

Graph of the function ${\displaystyle f_{1}}$

The function

${\displaystyle f_{1}(x,y)={\begin{cases}{\dfrac {2xy}{x^{2}+y^{2}}}&(x,y)\neq (0,0)\\0&(x,y)=(0,0)\end{cases}}}$

is partially differentiable at the point (0,0). The function has the constant value 0 on the coordinate axes, i.e. for all and applies ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle f_{1}(x,0)=f_{1}(0,y)=0}$.

It follows

${\displaystyle {\frac {\partial f_{1}}{\partial x}}(0,0)={\frac {\partial f_{1}}{\partial y}}(0,0)=0}$.

However, the function is not continuous at (0,0). On the first bisector (with the exception of the origin) has a constant value of one ( ). If one approaches the origin on the first bisector, the function values ​​therefore tend towards 1. The directional derivatives in other directions than those of the coordinate axes do not exist. ${\displaystyle f_{1}}$ ${\displaystyle f_{1}(t,t)=1}$

Graph of the function ${\displaystyle f_{2}}$

The function

${\displaystyle f_{2}(x,y)={\begin{cases}{\dfrac {2xy}{\sqrt {x^{2}+y^{2}}}}&(x,y)\neq (0,0)\\0&(x,y)=(0,0)\end{cases}}}$

is partially differentiable and continuous at the point (0,0). All unilateral directional derivations exist, but except in the coordinate directions not the bilateral ones.

Unilateral, but not bilateral directional derivatives

Graph of the function ${\displaystyle f_{3}}$

The Euclidean norm

${\displaystyle f_{3}(x,y)={\sqrt {x^{2}+y^{2}}}}$

generalizes the amount function . It is constant everywhere.

The one-sided directional derivative of in exists for every unit vector and it applies ${\displaystyle v=(v_{1},v_{2})\in \mathbb {R} ^{2}}$ ${\displaystyle f_{3}}$ ${\displaystyle (0,0)}$

${\displaystyle D_{v}^{+}f_{3}(0,0)=\lim _{h\searrow 0}{\frac {\sqrt {(hv_{1})^{2}+(hv_{2})^{2}}}{h}}=\lim _{h\searrow 0}{\frac {|h|}{h}}{\sqrt {v_{1}^{2}+v_{2}^{2}}}=\lim _{h\searrow 0}{\frac {|h|}{h}}=1}$

The limit value only exists on one side, so the directional derivatives on both sides do not exist. In particular, the function is also not partially differentiable.

All direction derivatives exist but do not define a linear mapping

Graph of the function ${\displaystyle f_{4}}$

${\displaystyle f_{4}(x,y)={\begin{cases}{\dfrac {3x^{2}y-y^{3}}{x^{2}+y^{2}}}&(x,y)\neq (0,0)\\0&(x,y)=(0,0)\end{cases}}}$

Here all directional derivatives exist for which partial derivatives apply

${\displaystyle {\frac {\partial f_{4}}{\partial x}}(0,0)=0,\ {\frac {\partial f_{4}}{\partial y}}(0,0)=-1.}$

However, the mapping is not linear. The following applies to the unit vector ${\displaystyle v\mapsto D_{v}f_{4}(0,0)}$ ${\displaystyle v=\left({\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)}$

${\displaystyle D_{\left({\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)}f_{4}(0,0)=0,}$

while

${\displaystyle {\frac {\partial f_{4}}{\partial x}}(0,0)\cdot {\frac {1}{2}}+{\frac {\partial f_{4}}{\partial y}}(0,0)\cdot {\frac {\sqrt {3}}{2}}=-{\frac {\sqrt {3}}{2}}.}$

All direction derivations exist and define a linear mapping, but not totally differentiable

Graph of the function ${\displaystyle f_{5}}$

${\displaystyle f_{5}(x,y)={\begin{cases}{\dfrac {xy^{3}}{x^{2}+y^{4}}}&(x,y)\neq (0,0)\\0&(x,y)=(0,0)\end{cases}}}$

Here there are all directional derivatives, for each vector applies . In particular, is partially differentiable with ${\displaystyle v\in \mathbb {R} ^{2}}$ ${\displaystyle D_{v}f_{5}(0,0)=0}$ ${\displaystyle f_{5}}$

${\displaystyle {\frac {\partial f_{5}}{\partial x}}(0,0)={\frac {\partial f_{5}}{\partial y}}(0,0)=0}$

and the figure

${\displaystyle v\mapsto D_{v}f_{5}(0,0)=0}$

is the zero mapping, so trivially linear.

The function is also continuous. However, it is not totally differentiable at the point (0,0). If it were, there would be zero figure and for each vector would apply ${\displaystyle L=Df(0,0)}$ ${\displaystyle v=(v_{1},v_{2})}$

${\displaystyle f_{5}(v_{1},v_{2})=f_{5}(0,0)+L(v_{1},v_{2})+r(v_{1},v_{2})=0+0+r(v_{1},v_{2})}$.

So it would apply to the error term ${\displaystyle r(v)=r(v_{1},v_{2})}$

${\displaystyle r(v_{1},v_{2})={\frac {v_{1}v_{2}^{3}}{v_{1}^{2}+v_{2}^{4}}}}$.

If you put and with , you get ${\displaystyle v_{1}=h^{2}}$ ${\displaystyle v_{2}=h}$ ${\displaystyle h>0}$

${\displaystyle r(v)={\frac {h^{2}h^{3}}{h^{4}+h^{4}}}={\frac {h}{2}}}$and so . ${\displaystyle \|v\|={\sqrt {h^{4}+h^{2}}}=h{\sqrt {1+h^{2}}}}$ ${\displaystyle {\frac {r(v)}{\|v\|}}={\frac {1}{2{\sqrt {1+h^{2}}}}}}$

For towards 0 this term goes towards instead of towards 0. ${\displaystyle h}$ ${\displaystyle {\tfrac {1}{2}}}$

Totally differentiable, but not continuously partially differentiable

Graph of the function ${\displaystyle f_{6}}$

This function is modeled on the corresponding example function of a variable, the verification is basically the same as there.

${\displaystyle f_{6}(x,y)={\begin{cases}(x^{2}+y^{2})\sin {\dfrac {1}{x^{2}+y^{2}}}&(x,y)\neq (0,0)\\0&(x,y)=(0,0)\end{cases}}}$

The function is totally differentiable at the point (0,0), the derivative is the null function . If one approaches the zero point, however, the partial derivatives diverge, for example the absolute value goes from

${\displaystyle {\frac {\partial f_{6}}{\partial x}}(x,0)=2x\sin {\dfrac {1}{x^{2}}}-{\frac {2}{x}}\cos {\dfrac {1}{x^{2}}}}$

towards infinity for towards 0. ${\displaystyle x}$

Mappings between finite-dimensional vector spaces

A mapping of an open set into vector space can be represented by its component functions: ${\displaystyle F}$ ${\displaystyle U\subset \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{m}}$

${\displaystyle F(x)=\left(f_{1}(x),\dots ,f_{m}(x)\right)}$with for . ${\displaystyle f_{i}\colon U\to \mathbb {R} }$ ${\displaystyle i=1,\dots ,m}$

Differentiability of can then be traced back to differentiability of . is (in the point ) partially differentiable (differentiable in the direction of the vector , totally differentiable, continuously partially differentiable) if all component functions have this property. ${\displaystyle F}$ ${\displaystyle f_{i}}$ ${\displaystyle F}$ ${\displaystyle a\in U}$ ${\displaystyle v}$ ${\displaystyle f_{1},\dots ,f_{m}}$

If the point is totally differentiable, then there is a linear mapping from to . Your representation matrix, the Jacobi matrix, consists of the partial derivatives ${\displaystyle F}$ ${\displaystyle a}$ ${\displaystyle DF(a)}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{m}}$

${\displaystyle J_{F}(a)={\begin{pmatrix}{\frac {\partial f_{1}}{\partial x_{1}}}&\dots &{\frac {\partial f_{1}}{\partial x_{n}}}\\\vdots &&\vdots \\{\frac {\partial f_{m}}{\partial x_{1}}}&\dots &{\frac {\partial f_{m}}{\partial x_{n}}}\end{pmatrix}}}$

and the directional derivative of in point in direction is the image of the vector under the linear map . ${\displaystyle F}$ ${\displaystyle a}$ ${\displaystyle v}$ ${\displaystyle v}$ ${\displaystyle DF(a)}$

Functions and mappings on infinite-dimensional vector spaces

There are no coordinates on infinite-dimensional vector spaces, so there is no partial differentiability. The terms directional derivation and total differentiability can, however, be generalized to infinitely dimensional vector spaces. In contrast to finite dimensions, the topology on the vector spaces plays an important role. Typical examples of infinite-dimensional vector spaces are function spaces, that is, vector spaces whose “vectors” are functions. To differentiate, the functions defined on these vector spaces are called functionals and mappings between such vector spaces are called operators.

Gâteaux differentiability

→ Main article: Gâteaux differential

The directional derivation corresponds to the Gâteaux derivation. Given is a normalized vector space (that is, a (typically infinite-dimensional) vector space together with a norm ), an open subset and a functional . The Gâteaux derivative of at a “point” in the direction of a vector is then given by ${\displaystyle V}$ ${\displaystyle \|\cdot \|}$ ${\displaystyle U\subset V}$ ${\displaystyle F\colon U\to \mathbb {R} }$ ${\displaystyle F}$ ${\displaystyle a\in U}$ ${\displaystyle v\in V}$

${\displaystyle \delta F(a,v)=\lim _{\tau \to 0}{\frac {F(a+\tau \,v)-F(a)}{\tau }}=\left.{\frac {\mathrm {d} }{\mathrm {d} \tau }}F(a+\tau \,v)\right|_{\tau =0}}$,

if the limit exists.

If the Gâteaux derivation for each exists, is a picture , explained. From the definition it follows immediately that this mapping is positively homogeneous, i.e. for all . As in finite dimensions, it does not follow from the existence of all directional derivatives that it is additive and thus linear. Even if the map is linear, it does not follow that it is continuous. ${\displaystyle v\in V}$ ${\displaystyle \delta F(a)\colon V\to \mathbb {R} }$ ${\displaystyle v\mapsto \delta F(a,v)}$ ${\displaystyle \delta F(a,\lambda v)=\lambda \delta F(a,v)}$ ${\displaystyle \lambda >0}$ ${\displaystyle \delta F(a)}$

There are several incompatible conventions for the term Gâteaux differentiability :

Some authors call a functional Gâteaux-differentiable at the point , if all exist, and then call the mapping a Gateaux derivative of at the point . Others additionally require that is linear and continuous. ${\displaystyle F}$ ${\displaystyle a}$ ${\displaystyle \delta F(a,v)}$ ${\displaystyle \delta F(a)}$ ${\displaystyle F}$ ${\displaystyle a}$ ${\displaystyle \delta F(a)}$

Similarly, one defines Gâteaux differentiability and Gâteaux derivation for operators from one normalized vector space into another normalized vector space (typically a Banach space ). The convergence required in the definition of the Gâteaux derivation is then understood in the sense of the norm of . The same applies to the continuity of . ${\displaystyle F}$ ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle W}$ ${\displaystyle \delta F(a)\colon V\to W}$

Fréchet differentiability

→ Main article: Fréchet derivation

The total differentiability in the finite-dimensional corresponds to the Fréchet differentiability in the case of infinite-dimensional vector spaces . Given are Banach spaces and , an open subset , a mapping and a point . ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle U\subset V}$ ${\displaystyle F\colon U\to W}$ ${\displaystyle a\in U}$

The mapping is called Fréchet-differentiable if a bounded (i.e. continuous) linear mapping and a mapping exist, so that with applies to all ${\displaystyle F}$ ${\displaystyle L\colon V\to W}$ ${\displaystyle r\colon U\to W}$ ${\displaystyle h\in V}$ ${\displaystyle a+h\in U}$

${\displaystyle F(a+h)=F(a)+L\,h+r(h)}$

and

${\displaystyle \lim _{\Vert h\Vert \to 0}{\frac {\|r(h)\|}{\Vert h\Vert }}=0.}$

The numerator contains the norm of and the denominator of . ${\displaystyle W}$ ${\displaystyle V}$

In this case, the linear operator is called the Fréchet derivative of at that point . ${\displaystyle L\colon V\to W}$ ${\displaystyle F}$ ${\displaystyle a}$

Connections

As in the finite-dimensional, every Fréchet-differentiable mapping is also Gâteaux-differentiable and the Gâteaux-derivative agrees with the Fréchet-derivative. Conversely, the point need not be Fréchet-differentiable even if the Gâteaux derivative is linear and continuous. ${\displaystyle F}$ ${\displaystyle F}$ ${\displaystyle a}$ ${\displaystyle \delta F(a)}$

Differentiable mappings between differentiable manifolds

The differentiability of images between differentiable manifolds is attributed to the differentiability of their map representations. Consistency has to be assumed here.

Let and be differentiable manifolds of the dimensions or and the differentiability class and let it be a continuous mapping. For each point there is then a map of um , i.e. an open environment that contains, and a homeomorphism defined on an open subset of the . There is also a map of around the pixel . Since is continuous, the cards can be chosen so that lies entirely in . The map representation of with regard to these maps is then understood to mean the illustration ${\displaystyle M}$ ${\displaystyle N}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle C^{r}}$ ${\displaystyle F\colon M\to N}$ ${\displaystyle p\in M}$ ${\displaystyle (U,\phi )}$ ${\displaystyle M}$ ${\displaystyle p}$ ${\displaystyle U\subset M}$ ${\displaystyle p}$ ${\displaystyle U}$ ${\displaystyle \phi \colon U\to \phi (U)\subset \mathbb {R} ^{m}}$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle (V,\psi )}$ ${\displaystyle N}$ ${\displaystyle f(p)\in N}$ ${\displaystyle F}$ ${\displaystyle F(U)}$ ${\displaystyle V}$ ${\displaystyle F}$

${\displaystyle \psi \circ F\circ \phi ^{-1}\colon \phi (U)\to \psi (V)}$

This is a mapping from the open subset of to the open subset of . ${\displaystyle \phi (U)}$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle \psi (V)}$ ${\displaystyle \mathbb {R} ^{n}}$

The mapping is called continuously differentiable if it is continuous and its map representations are continuously differentiable. It is called - sometimes continuously differentiable (for ), or by the class , if its map displays - sometimes continuously differentiable. ${\displaystyle F}$ ${\displaystyle k}$ ${\displaystyle k\leq r}$ ${\displaystyle C^{k}}$ ${\displaystyle k}$

The differentiability does not depend on the choice of cards (as long as is), since the map change maps - are diffeomorphisms . If or is the Euclidean space , you can do without the map there. In particular: ${\displaystyle k\leq r}$ ${\displaystyle C^{r}}$ ${\displaystyle M}$ ${\displaystyle N}$

A function is then and only continuously differentiable if this applies to its map representations with regard to maps of . ${\displaystyle f\colon M\to \mathbb {R} }$ ${\displaystyle r}$ ${\displaystyle f\circ \phi ^{-1}\colon \phi (U)\to \mathbb {R} }$ ${\displaystyle (U,\phi )}$ ${\displaystyle M}$

Analogously, one defines the complex differentiability for complex-valued functions on complex manifolds and mappings between complex manifolds.

For the definition of the derivative of a mapping between manifolds or a function on a manifold, see tangent space and pushforward . ${\displaystyle F}$ ${\displaystyle f}$

Term extensions

The following concepts are generalizations of differentiability:

• weak derivatives
• Differentiability in the sense of distributions
• Radon-Nikodým derivative

Web links

Commons : Differentiability  - collection of images, videos and audio files

Wikibooks: Math for Non-Freaks: Derivation and Differentiability  - Learning and Teaching Materials

Individual evidence

1. ↑ Guido Walz (Ed.): Lexicon of Mathematics . 2nd edition volume 3 (Inp to Mon). Springer Spektrum Verlag, Mannheim 2017, ISBN 978-3-662-53501-1 , p. 148 f ., doi : 10.1007 / 978-3-662-53502-8 .

literature

In principle all introductory literature on analysis and / or differential calculus. For example:

• Otto Forster : Analysis 1. Differential and integral calculus of a variable. 7th edition. Vieweg, Braunschweig 2004, ISBN 3-528-67224-2 .
• Otto Forster: Analysis 2. Differential calculus in R ⁿ . Ordinary differential equations. 6th edition. Vieweg, Braunschweig 2005, ISBN 3-528-47231-6 .
• Konrad Königsberger : Analysis. 2 volumes. Springer, Berlin 2004, ISBN 3-540-41282-4 .