Distribution (math)
In the field of mathematics, a distribution describes a special type of functional , i.e. an object from functional analysis .
The theory of distributions makes it possible to define a type of solution for differential equations which in the classical sense are not sufficiently often differentiable or not defined at all (see distributional solution ). In this sense, distributions can be viewed as a generalization of the notion of function . There are partial differential equations that have no classical solutions , but solutions in the distributional sense. The theory of distributions is therefore particularly important in physics and engineering : many of the problems examined there lead to differential equations that could only be solved with the help of the theory of distributions.
The mathematician Laurent Schwartz was instrumental in studying the theory of distributions. In 1950 he published the first systematic approach to this theory. He received the Fields Medal for his work on the distributions .
History of Distribution Theory
In 1903 Jacques Hadamard introduced the concept of the functional, which is central to distribution theory . From today's perspective, a functional is a function that assigns a number to other functions. Hadamard was able to show that every continuous , linear functional as the limit value of a sequence of integrals
can be represented. In general, limit value and integral must not be interchanged in this representation. In 1910 it could be shown that every continuous, linear functional on , the space of p-integrable functions , as
can be displayed with and . With this formulation, no limit value has to be established and is clearly defined. That is why the functional is often identified with the "function" . Then has two different meanings: On the one hand, one understands as - "function" , on the other hand it is equated with the functional .
The first dealt Paul Dirac in the 1920s for research in quantum mechanics with distributions. He introduced the important delta distribution . However, he did not yet use a mathematically precise definition for this distribution. In his investigations, he disregarded the functional analysis of the time, i.e. the theory of the functional. In the 1930s Sergei Lwowitsch Sobolew dealt with initial value problems in partial hyperbolic differential equations . For these investigations he introduced the Sobolew rooms, which are named after him today . In 1936, Sobolev was studying hyperbolic second order differential equations with analytic coefficient functions . In order to be able to specify a more handy criterion for the existence of a solution to this partial differential equation, Sobolew extended the question to the space of the functional. He was the first to formulate today's definition of a distribution. However, he did not yet develop a comprehensive theory from his definitions, but only used it as an aid to investigating partial differential equations.
Finally Laurent Schwartz developed the theory of distributions in the winter of 1944/45. At this point in time Sobolev's work was still unknown to him, but just like Sobolew, through questions in the area of partial differential equations, he too came across special functionals, which he now called distributions. From then on, the theory was further developed so quickly that Schwartz was able to give lectures on it in Paris in the winter of 1945/46. Electrical engineers attending his lectures urged him to further develop his theory in the direction of Fourier and Laplace transforms . In 1947 Schwartz had defined the space of tempered distributions and thus integrated the Fourier transformations into his theory. In 1950/51 his monograph Theory of Distribution appeared, which further strengthened his theory. As early as 1950 he received the Fields Medal , one of the highest awards in the field of mathematics, for his research in the field of distributions .
From then on, the theory of distributions was further developed in theoretical physics and in the theory of partial differential equations . Distribution theory is useful for describing singular objects in physics such as the electromagnetic point charge or the point mass with mathematical precision. These two physical objects can be suitably described with the help of the delta distribution, because the spatial density function of a mass point with unit mass is required to vanish everywhere except at one point. There it has to become infinite, since the space integral over the density function should result in 1 (unit mass). There is no function in the usual sense that fulfills these requirements. In the theory of partial differential equations and Fourier analysis , distributions are important, since with this concept formation every locally integrable function can be assigned a derivative.
Definitions
distribution
Be an open, non-empty set. A distribution is a continuous and linear functional in the space of the test functions .
In other words, a picture or so for all and true
and
whenever in .
Room of the distributions
The set of distributions with the corresponding links of addition and scalar multiplication is thus the topological dual space to the test function space and is therefore noted as. In functional analysis, the symbol denotes the topological dual space. In order to be able to speak of continuity and topological dual space at all, the space of the test functions must be equipped with a locally convex topology.
The following characterization is therefore often used as an alternative definition, since it does without the topology of the test function space and no knowledge of locally convex spaces is required:
Be an open crowd. A linear functional is called distribution if for every compact there is one and one , so that the inequality for all test functions
applies. This definition is equivalent to the one given before, because the continuity of the functional follows from this inequality, although it does not have to apply to the whole , because the (LF) -space is bornological .
Order of a distribution
If the same number can be chosen for all compacts in the alternative definition above , the smallest possible number is called the order of . The set of distributions of the order is denoted by and the set of all distributions with finite order is noted with. This space is smaller than the general distribution space , because there are also distributions that are not of finite order.
Regular distribution
The regular distributions are a special subset of the distributions. These distributions are generated by a locally integrable function . Precisely this means that a distribution is called regular if there is a representation
where there is a locally integratable function. Non-regular distributions are also called singular ; these are distributions for which there is no generating function in the sense of this definition.
This integral representation of a regular distribution, together with the scalar product im, motivates the alternative notation
for all (not just regular) distributions.
Test functions
In the definition of the distribution, the concept of the test function or the test function space is central. This test function space is the space of smooth functions with compact support together with an induced topology . Choosing a topology on the test function space is very important because otherwise the concept of continuity cannot be meaningfully defined. The topology is defined in space by a concept of convergence.
Let be an open subset , then denoted
the set of all infinitely often differentiable functions that have a compact support , i.e. that are zero outside of a compact set. The concept of convergence is defined by defining: A sequence with converges against , if there is a compact word with for all and
for all multi-indices . The set is - endowed with this concept of convergence - a locally convex space , which one calls the space of the test functions and is noted as.
Two different points of view
As described above in the section on the definition of the distribution, a distribution is a functional , i.e. a function with certain additional properties. In the section History of Distribution Theory, however, it was said that the delta distribution cannot be a function. This is obviously a contradiction that can still be found in current literature. This contradiction arises from the attempt to identify distributions - and also functionals tidy up - with real-valued functions.
In theoretical physics in particular, a distribution is understood to be an object, named for example , with certain properties resulting from the context. The desired properties often prevent a function from being able to exist, which is why one speaks of a generalized function. Now that the properties of have been determined, consider the assignment
which assigns a real number to a test function . However, since there is generally no function, a meaning must first be explained for the expression on a case-by-case basis.
From a mathematical point of view, a distribution is a function with certain abstract properties (linearity and continuity) that assigns a real number to a test function. If this is an integrable function from the previous paragraph, the expression is mathematically precisely defined. However, the function is not referred to as distribution here , but the functional is called distribution.
Also, many mathematics textbooks do not differentiate between the (distribution) generating function and the actual distribution in the mathematical sense. For the most part, this article uses the more rigorous mathematical perspective.
Examples
Continuous function as a producer
Be and , so is through
one distribution defined for all .
Delta distribution
The delta distribution is a singular distribution. That is, it cannot be generated by an ordinary function, although it is often written like one. The following applies:
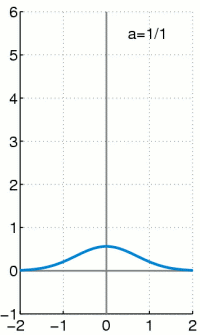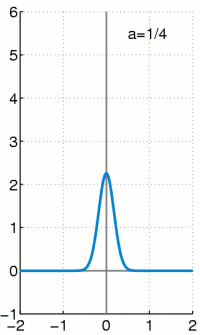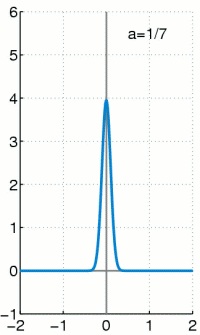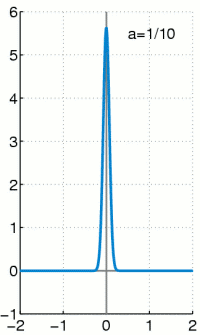
That is, the delta distribution applied to a test function gives the value of the test function at the position 0. Just like any other distribution, the delta distribution can also be expressed as a sequence of integral terms. The Dirac episode
has the limit value (compare e.g. the adjacent animation)
which would lead to the vanishing integral . Because the behavior in only one point is irrelevant for integrals of ordinary functions.
With this Dirac sequence, however, the delta distribution can be carried out with a different limit value formation, before the integral and not after it
represent. Mostly, however, the symbolic spelling is used, which leads to mathematically imprecise interpretation
used for the delta distribution, calling the term a generalized function and often omitting the word generalized .
Dirac comb
The Dirac comb with is a periodic distribution that is closely related to the Dirac delta distribution. This distribution is defined for everyone as
This series converges because the test function has compact support and therefore only a finite number of summands are not equal to zero. An equivalent definition is
where the equal sign is to be understood as equality between distributions. The row on the right then converges on the weak - * topology . The convergence of distributions is discussed in more detail in the section Convergence . The one appearing in the definition is a real number called the period of the Dirac ridge. The Dirac ridge is clearly composed of an infinite number of delta distributions that are at a distance from one another. In contrast to the Delta distribution, the Dirac comb does not have a compact carrier. What this means exactly is explained in the Compact Carrier section below.
Radon measures
With is the amount of all radon measures. Be Well you can by
assign a distribution to each . In this way you can steadily in embedding . An example of a radon measure is the Dirac measure . For everyone it is defined by
One identifies the Dirac measure with the generating distribution
so one gets the delta distribution, if holds.
Cauchy's principal value of 1 / x
The main Cauchy value of the function can also be viewed as a distribution . You bet for everyone
This is a singular distribution, since the integral expression is not defined in Lebesgue's sense and only exists as a main Cauchy value. The abbreviation PV stands for principal value.
This distribution is mostly used together with the dispersion relation ( Plemelj-Sokhotsky formula ), whereby all distributions, in particular and as indicated, are expressed by generalized functions and denote the imaginary unit. In linear response theory, this relationship connects the real and imaginary parts of a response function, see Kramers-Kronig relationships . (At this point it is assumed that the test functions are complex, so , and so are the response functions just mentioned; but the argument should still be real, although of course it is complex, and not real.)
Oscillating integral
For all symbols one calls
an oscillating integral. Depending on the choice of, this integral type does not converge in the Riemann or Lebesgue sense, but only in the sense of distributions.
convergence
Since the distribution space is defined as a topological dual space , it also has a topology . As a dual space of a Montel space , provided with the strong topology , it is itself a Montel space, so the strong topology coincides with the weak - * topology for consequences . The following concept of convergence arises for sequences: A sequence of distributions converges to if the equation for each test function
applies.
Because each test function with can be identified, of as a topological subspace be construed.
The room is close in . This means that there is a sequence of test functions in with in for each distribution . So you can go through any distribution
represent.
Localization
Restriction to a subset
Be open subsets and be a distribution. The restriction from to the subset is defined by
for all , where that is continued through zero .
carrier
Be a distribution. It is said that a point belongs to the bearer of and writes if a function exists for every open environment of .
If a regular distribution is continuous , then this definition is equivalent to the definition of the carrier of a function (the function ).
Compact carrier
A distribution has a compact carrier if there is a compact space . The set of distributions with compact carriers is denoted by. It is a sub-vector space from and the topological dual space to , the space of smooth functions . This space is made by the family of semi-norms
- ,
where takes on arbitrary values and passes through all compact subsets of , generating a locally convex topology .
Singular carrier
Be a distribution. It is said that a point does not belong to the singular carrier if there is an open environment of and a function with
for everyone .
In other words: if and only if there is no open environment of , so that the restriction of on equals a smooth function. In particular, the singular carrier of a singular distribution is not empty.
Operations on distributions
Since the distribution space with pointwise addition and multiplication with complex numbers is a vector space over the field , the addition of distributions and the multiplication of a complex number with a distribution are already defined.
In the following, further operations on distributions such as the derivation of a distribution are explained. Many operations are carried over to distributions by applying the appropriate operation to the test functions. For example, if a linear map, the one - test function to a mapping function, and there is also still a adjoint linear and follow continuous map such that for all test functions and applies
- ,
then
a well-defined operation on distributions.
Multiplication by a function
Be and . Then the distribution is defined by
- .
Differentiation
motivation
If one considers a continuously differentiable function and the regular distribution assigned to it, one obtains the calculation rule
Here was partial integration used, the boundary terms because of the selected properties of the test function no longer apply. This corresponds to the weak derivative . The two outer terms are also defined for singular distributions. One uses this to define the derivative of any distribution .
definition
So be a distribution, a multi-index and . Then the distribution derivative is defined by
- .
In the one-dimensional case, this just means
- .
The notation is often used for the distribution derivation .
example
The Heaviside function is through
Are defined. With the exception of the position, it can be differentiated everywhere. You can think of it as a regular distribution and the bill
shows that its derivative (as distribution) is the delta distribution :
You can also derive the delta distribution itself:
Except for the additional sign factor , the derivatives of the delta distribution are therefore the same as the derivatives of the test function at that point
Tensor product
motivation
Be the set as a product space with given. Then you can click on the functions and by means of the regulation
define a tensor product . Similarly, one can define a tensor product between distributions. For this purpose, regular distributions are first considered. Let and be two locally integrable functions, it follows from the above definition
for all it follows
The following definition is derived from this:
definition
Be and . Then a distribution is made through
is defined.
Smoothing a distribution
Distributions can be specifically smoothed or smeared or approximated , e.g. B. by replacing the distribution with the regular distribution of a smooth approximation function, such as B. the distribution through the regular distribution
the function defined above or the Heaviside distribution through the regular distribution of the integrals of such functions. With three-dimensional differential equations one can B. determine whether the boundary conditions match the differential equations that apply to the interior. This is useful for many applications, especially since the smoothing functions, except for the limit, are not clearly specified, which leads to increased flexibility. You can also regularize distributions like the above PV distribution in a targeted manner. B. provides the test functions with suitable factors or proceeds in another way.
Folding with one function
definition
Let be a distribution and a function, then the convolution of with is defined by
- .
example
Let be a radon measure and be the distribution identified with the radon measure. Then applies to the convolution of with
properties
- If is a smooth function, then the definition agrees with the convolution of functions.
- The result of the convolution is a smooth function, so the following applies
- .
- For and , the convolution is associative, that is, it applies
- .
- For each multi-index , the derivative of the convolution applies
- .
Convolution of two distributions
definition
Be and two distributions, at least one of which has compact carriers. Then for all the convolution between these distributions is defined by
- .
The image
is linear, continuous and commutes with displacements. Therefore there is a unique distribution so
applies to all .
Note: The condition that a distribution has compact carriers can be weakened even further.
properties
This definition is a generalization of the definitions already mentioned here. If you choose a function for a regular distribution, this corresponds to the definitions listed here. The following properties apply:
- The convolution is commutative:
- The following applies to the carrier:
- For the singular carrier we get:
Tempered distributions
The tempered distributions form an excellent subset of the distributions in space considered so far . On the tempered distributions it is possible to explain the Fourier and Laplace transforms.
Fourier transform
In order to be able to define a Fourier transform on distributions, one must first restrict the set of distributions. Not every function is Fourier transformable, and in the same way one cannot explain the Fourier transform for every distribution. For this reason Laurent Schwartz developed the Schwartz space , which is named after him today , by defining this space using a family of semi-norms that are symmetrical in terms of multiplication with the position variable and differentiation according to them. Because the Fourier transform swaps differentiation with and multiplication with , this symmetry implies that the Fourier transform of a Schwartz function is again a Schwartz function. In this space, the Fourier transformation is therefore an automorphism , i.e. a continuous, linear and bijective mapping to itself. The topological dual space , i.e. the space of the continuous, linear functionals of , is called the space of tempered distributions. The set of tempered distributions is larger than the set of distributions with compact support, which is due to the fact that the set of Schwartz functions is a subset of the space of smooth functions. The smaller a function space, the larger its dual space. Therefore, the amount of temperature-controlled distributions in the room is also included. Because the set of smooth functions with a compact carrier is a subset of the Schwartz space.
The Fourier transform of can for all by
To be defined. The Fourier transform is also an automorphism. The Fourier transform of the delta function is a constant distribution . Another example of a tempered distribution is the Dirac comb mentioned above.
Convolution theorem
In connection with the above definitions of the convolution of two distributions and the Fourier transform of a distribution, the convolution theorem is interesting, which can be formulated as follows:
Let be a tempered distribution and a distribution with a compact carrier, then and the convolution theorem for distributions says:
The multiplication of two distributions is generally not defined. In this particular case, however, makes sense because it is a smooth function.
Differential equations
Since every locally integrable function, in particular every function, generates a distribution, one can assign a distribution as a derivative to these functions in the weak sense . If distributions are allowed as a solution to a differential equation , the solution space of this equation increases. In the following it is shown briefly what a distributional solution of a differential equation is and how the fundamental solution is defined.
Solutions in the distribution sense
Be
a differential operator with smooth coefficient functions . A distribution is called a distribution solution by if the distributions created by and match. this means
for everyone . If the distribution is regularly and even continuously differentiable, then a classical solution of the differential equation is.
example
Constant functions
All distributional solutions of the one-dimensional differential equation
are the constant functions. That is, for everyone the equation will
only solved by constant .
Poisson's equation
A prominent example is formal identity
from electrostatics , with the Laplace operator . That means precise
This means
is a solution to Poisson's equation for all
It is also said that the Poisson equation considered here solves in the distributional sense.
Fundamental solutions
Be now a linear differential operator. A distribution is called a fundamental solution if the differential equation
solves in the sense of distribution.
The set of all fundamental solutions of results from adding a special fundamental solution to the general homogeneous solution . The general homogeneous solution is the set of distributions for which holds. According to a theorem of Bernard Malgrange , every linear differential operator with constant coefficients has a fundamental solution .
With the help of these fundamental solutions, solutions of corresponding inhomogeneous differential equations are obtained by convolution. Let be a smooth function (or, more generally, a distribution with compact support), then because of
a solution of in the form
where is a fundamental solution of the differential operator just like above.
Harmonious distributions
Analogous to the harmonic functions , one also defines harmonic distributions. So a distribution is called harmonic if it follows the Laplace equation
in the distributional sense is sufficient. Since the distributional derivative is more general than the ordinary differential , one might expect more solutions to Laplace's equation. However, this is wrong. Because one can prove that for every harmonic distribution there is a smooth function that produces that distribution. So there are no singular distributions that satisfy the equation; in particular, the singular carrier of a harmonic distribution is empty. This statement is even more general for elliptic partial differential equations . For physicists and engineers, this means that they can safely work with distributions in electrodynamics , for example in the theory of Maxwell's equations , even if they are only interested in ordinary functions.
Distributions as integral kernels
You can go through every test function
identify with an integral operator . This identification can be extended to distributions. So there is a linear operator for every distribution
for everyone and through
given is. The reverse direction also applies. So there is a unique distribution for each operator so that applies. This identification between operator and distribution is the message of Schwartz's core theorem. The distribution also bears the name Schwartz kernel based on the concept of the integral kernel . However, the operator cannot always be represented in the form of an integral term.
Distributions on Manifolds
Return transport
Distributions can be transported back and forth on real subsets with the help of diffeomorphisms . Let be two real subsets and a diffeomorphism, i.e. a continuously differentiable, bijective function whose inverse mapping is also continuously differentiable. The equation applies to and for all test functions due to the transformation theorem
This identity motivates the following definition for the concatenation of a distribution with a diffeomorphism: Let , then is defined for all by
Mostly it is noted as and is called the return transport of the distribution
definition
Be a smooth manifold , a system of cards, and such that for all
in applies. Then the system is called a distribution . This distribution is clearly defined and independent of the choice of card.
There are other ways to define distributions on manifolds. The definition in connection with density bundles has the advantage that no system of local maps has to be selected there.
Regular distributions on manifolds
With this definition one can again assign a distribution to every continuous function by means of the integral representation. So be a continuous function on the manifold, then there is a continuous function on . Using the integral representation for regular distributions
you get a system that forms a distribution on .
Individual evidence
- ^ Paul Adrien Maurice Dirac: The principles of quantum mechanics. Clarendon Press, 1947.
- ↑ Sergei Lwowitsch Sobolew: Méthode nouvelle à résoudre leproblemème de Cauchy pour les équations linéaires hyperboliques normales. Mat. Sb. 1, 1936, pp. 39-72.
- ^ Laurent Schwartz: Théorie des distributions 1–2. Hermann, 1950–1951.
- ^ Laurent Schwartz: Théorie des distributions. 1-2, p. 74, Hermann, 1950-1951.
- ^ Lars Hörmander : The Analysis of Linear Partial Differential Operators. Volume 1: Distribution Theory and Fourier Analysis. Second edition. Springer-Verlag, Berlin et al. 1990, ISBN 3-540-52345-6 ( Basic Teachings of Mathematical Sciences 256), p. 41.
- ^ Lars Hörmander : The Analysis of Linear Partial Differential Operators. Volume 1: Distribution Theory and Fourier Analysis. Second edition. Springer-Verlag, Berlin et al. 1990, ISBN 3-540-52345-6 ( Basic Teachings of Mathematical Sciences 256), pp. 41–42.
- ^ Lars Hörmander : The Analysis of Linear Partial Differential Operators. Volume 1: Distribution Theory and Fourier Analysis. Second edition. Springer-Verlag, Berlin et al. 1990, ISBN 3-540-52345-6 ( Basic Teachings of Mathematical Sciences 256), p. 42.
literature
-
Israel Gelfand : Generalized Functions (Distributions). VEB Deutscher Verlag der Wissenschaften, Berlin (East).
- Volume 1: IM Gelfand, GE Schilow : Generalized functions and calculating with them. 1960 ( University books for mathematics 47, ISSN 0073-2842 ).
- Volume 2: IM Gelfand, GE Schilow: Linear topological spaces, spaces of basic functions and generalized functions. 1962 ( University books for mathematics 48).
- Volume 3: IM Gelfand, GE Schilow: Some questions about the theory of differential equations. 1964 ( University books for mathematics 49).
- Volume 4: IM Gelfand, NJ Wilenkin : Some Applications of Harmonic Analysis. Gelfandian space triple. 1964 ( university books for mathematics 50).
- Only in Russian: Обобщенные функции. Том 5: И. М. Гельфанд, М. И. Граев, Н. Я. Виленкин: Интегральная геометрия и связанные с ней вопросы теории представлений. Гос. Изд. Физ.-Мат. Лит., Москва 1962.
- Lars Hörmander : The Analysis of Linear Partial Differential Operators. Volume 1: Distribution Theory and Fourier Analysis. Second edition. Springer-Verlag, Berlin a. a. 1990, ISBN 3-540-52345-6 ( Basic Teachings of the Mathematical Sciences 256).
- MJ Lighthill : An introduction to Fourier analysis and generalized functions. Reprinted. Cambridge University Press, Cambridge 2003, ISBN 0-521-09128-4 (Cambridge monographs on mechanics and applied mathematics).
- Klaus-Heinrich Peters: The connection between mathematics and physics using the example of the history of distributions. A historical study of the fundamentals of physics at the border with mathematics, philosophy and art. Hamburg 2004 (Hamburg, Univ., Diss., 2004).
- VS Vladimirov : Generalized function. In: Michiel Hazewinkel : Encyclopaedia of Mathematics . Springer-Verlag, Berlin a. a. 2001, ISBN 1-55608-010-7 .
- Joseph Wloka: Basic Spaces and Generalized Functions. Springer-Verlag, Berlin a. a. 1969 ( Lecture notes in mathematics. 82, ISSN 0075-8434 ).