Local convex room

Local convex spaces (more precisely: locally convex topological vector spaces ) are topological vector spaces with additional properties that are examined in the mathematical subfield of functional analysis . These are topological vector spaces in which each point has "arbitrarily small" convex neighborhoods . Alternatively, locally convex spaces can also be defined as vector spaces, the topology of which is generated by a family of semi-norms .

The unit sphere in Euclidean space is a convex neighborhood of zero.

A locally convex space can be viewed as a generalization of a normalized vector space or a normalizable vector space , because the standard spheres around 0 are convex surroundings of the zero point.

Geometric definition

A topological vector space (over the field of real numbers or the field of complex numbers ) is called locally convex if every zero neighborhood (i.e. neighborhood of the zero point) contains an open subset with the following three properties: ${\displaystyle V}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle U}$ ${\displaystyle T}$

• ${\displaystyle T}$ is convex.
• ${\displaystyle T}$is absorbent .
• ${\displaystyle T}$is balanced .

A subset of a real or complex vector space is thereby absorbing , if for every vector in a positive number is such that for any real or complex number with an element of is. ${\displaystyle T}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle V}$ ${\displaystyle r}$ ${\displaystyle \alpha x}$ ${\displaystyle \alpha }$ ${\displaystyle |\alpha |<r}$ ${\displaystyle T}$

A subset of a real or complex vector space is called balanced if for every vector in and every number with the vector is also in . In the case of a real vector space, this means that the distance from to in lies; in the case of a complex vector space it means that the “circular disk” contains. Because of this geometric meaning, such sets are sometimes called circular . ${\displaystyle T}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle T}$ ${\displaystyle r}$ ${\displaystyle |r|\leq 1}$ ${\displaystyle rx}$ ${\displaystyle T}$ ${\displaystyle -x}$ ${\displaystyle x}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle \{rx\mid r\in \mathbb {C} ,\ |r|\leq 1\}}$

A balanced and convex set is called an absolutely convex set .

It turns out that the second and third conditions can be dispensed with. There is a zero neighborhood basis composed of convex, absorbent, and balanced sets if and only if there is a null neighborhood basis composed of convex sets. Of course, two such surrounding bases need not match, but the existence of one implies the existence of the other.

Definition by semi-norms

Locally convex spaces can also be characterized by semi-norms: A topological vector space is called locally convex if its topology is defined by a family of semi-norms . That is, a network converges if and only if it converges with respect to all semi-norms from ; more precisely: it is exactly if for all semi-norms . The spheres , where , form a sub-basis of the topology, the sets are absolutely convex zero environments. ${\displaystyle V}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle x_{i}\rightarrow x}$ ${\displaystyle p(x_{i}-x)\rightarrow 0}$ ${\displaystyle p\in {\mathcal {P}}}$ ${\displaystyle B_{p}(x,\varepsilon )=\left\{y\in V\,:\,p(x-y)<\varepsilon \right\}}$ ${\displaystyle x\in V,\,\varepsilon >0,\,p\in {\mathcal {P}}}$ ${\displaystyle B_{p}(0,\varepsilon )}$

Conversely, if a zero environment basis is given from absolutely convex sets, the associated Minkowski functionals form a defining semi-norms system.

Examples

1. All normalized spaces (especially all Banach spaces ) are locally convex, whereby the family only contains the (real) norm . ${\displaystyle {\mathcal {P}}}$
2. Direct Limites of Banach spaces such as the space of continuous functions with compact support on . ${\displaystyle \mathbb {R} }$
3. All topological vector spaces with the weak topology .
4. Banach spaces with weak topology as well as dual spaces of Banach spaces with weak - * - topology are locally convex, whereby the family is generated here by the functionals from the dual or predual space by means of ( y is the functional). ${\displaystyle {\mathcal {P}}}$ ${\displaystyle p_{y}\left(x\right)=|y(x)|}$
5. Projective limits of Banach spaces are locally convex. The family is given by the norms of the Banach areas, whose Limes is formed. As an example, consider with the family of norms Although the family consists of real norms, space is not a Banach space! ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {C}}^{\infty }([0,1])}$
   ${\displaystyle p_{k}(f)=\sum _{i\leq k}\max _{x\in [0,1]}|f^{(i)}(x)|.}$
   
6. Any products from Banach rooms, such as B. , the space of all functions from to with the topology of point-wise convergence. ${\displaystyle \mathbb {R} ^{\mathbb {R} }}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$
7. The Schwartz room , sequential rooms such as the Köthe rooms , function rooms such as rooms for test functions .
8. The space L ^p ([0,1]) is for a topological (even metrizable ) vector space that is not locally convex. ${\displaystyle 0<p<1}$
9. Likewise, the space of the random variables on a given probability space with the topology of stochastic convergence is a topological vector space that is generally not locally convex.

properties

If the semi-norm set from the above definition fulfills , the space is a Hausdorff space . Many authors only consider Hausdorff's locally convex spaces. ${\displaystyle \{x\in V:p(x)=0\;\forall \,p\in {\mathcal {P}}\}=\{0\}}$

Hausdorff locally convex spaces have enough continuous, linear functionals to separate points , i. H. for all there is a continuous, linear functional with . This shows in the validity of important sentences like ${\displaystyle x,y\in V,x\not =y}$ ${\displaystyle f}$ ${\displaystyle f(x)\not =f(y)}$

• The Hahn-Banach theorem
• The separation sentence
• The Kerin-Milman Theorem

The continuous, linear functionals on a topological vector space V separate the points if and only if there is a coarser topology on V that makes V a Hausdorffian, locally convex space. The investigation of locally convex spaces using continuous, linear functionals leads to a very far-reaching theory that is not possible for general topological vector spaces. There are topological vector spaces that have no other continuous, linear functional apart from the null functional.

Generalizations

• Topological vector space
• Topological group
• Uniform room

Special classes of locally convex spaces

Relationships between the room classes, an arrow leads from the more specific to the more general room class.

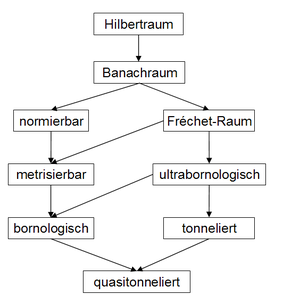
Many classes of locally convex spaces are characterized by the validity of certain propositions that are known from the theory of Banach spaces or normalized spaces. So are z. B. the barreled spaces are exactly those locally convex spaces in which the Banach-Steinhaus theorem still applies. These sentences can be examined in "pure culture" in the corresponding room classes, their scope becomes clear. The best known of these room classes are:

• bornological spaces and ultrabornological spaces
• barreled rooms and quasi-barreled rooms
• Metrizable locally convex spaces
• Fréchet rooms
• normalized vector spaces
• Banach rooms
• Hilbert dreams

Spaces with differentiable or holomorphic functions have natural locally convex topologies, the properties of which give rise to further room classes. The most important of these space classes, which lead to a deeper understanding of the locally convex theory, are approximately

• nuclear spaces
• Montel rooms
• Schwartz rooms
• (DF) rooms and gDF rooms
• quasi-normalizable spaces
• (LF) rooms and LB rooms
• Spaces with tissue

Historical remarks

As early as 1906 M. Fréchet found that the “closure” of the set of bounded continuous functions on in the set of all bounded functions on with respect to point-wise convergence cannot be described by the set of all limit values ​​from sequences . The more general concept of environment required for this, as it was introduced in 1914 by F. Hausdorff in the general topology, was first found in functional analysis by J. v. Neumann in his description of weak or strong zero environments , Hilbert space , application, wherein a generalization was not attempted to Banach. The concept of environment for more general situations can be found in S. Banach (1932) and Bourbaki (1938) in studies of the weak - * - topology , initially limited to separable spaces so that the unit sphere can be metrised in the dual space . Although the focus was on the investigation of standardized spaces, it was clear that more general room classes occur naturally. ${\displaystyle C_{b}(\mathbb {R} )}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle C_{b}(\mathbb {R} )}$ ${\displaystyle L(H)}$ ${\displaystyle H}$

S. Banach, S. Mazur and W Orlicz considered spaces whose topology is given by a sequence of semi-norms and defined the distance ${\displaystyle (p_{n})_{n}}$

${\displaystyle d(x,y):=\sum _{n=1}^{\infty }\,{\frac {1}{n!}}\cdot {\frac {p_{n}(x-y)}{1+p_{n}(x-y)}}}$.

The theorem of the closed graph could be proved for the complete ones among these spaces, which are now called Frécheträume . However, the observation of J. v. Neumanns from 1929 that the weak topology cannot be metrised on infinite-dimensional Hilbert spaces.

In 1934 G. Köthe and O. Toeplitz introduced new types of spaces, so-called sequence spaces , and developed their theory of duality in the context of sequence spaces. In this context the concept of the strong dual space emerged .

The sets restricted in the sense of the metric did not behave as in the case of standardized spaces; a topological characterization of the restrictedness was required, as described in the work J. v. Neumanns from 1935. This concept of limitation is also found in the same year by AN Kolmogorow in the proof of the statement that a Hausdorff topological vector space can be normalized precisely if it has a bounded and convex null neighborhood ( Kolmogorow's criterion for normalization ). Von Neumann's work also contains the general definition of locally convex space for the first time; the equivalence of the geometric definition given above and the definition by semi-norms is proven there. This enabled the ideas of Köthe and Toeplitz to be implemented in a more general framework. Milestones were the results of G. Mackey from 1946, see Mackey's theorem, Mackey-Arens ' theorem , and the investigations of tensor products by A. Grothendieck from 1953. The locally convex spaces gained further importance through von L. Schwartz , A. Grothendieck, SL Sobolew , S. Bochner and other investigations carried out in the theory of partial differential equations and the accompanying justification of the theory of distributions . The principle of the core led Grothendieck to the important concept of nuclear space .

See also

• Local convex algebras are local convex spaces with an algebra structure and conditions on multiplication.
• Normalized spaces with the weak topology , the weak - * topology or the restricted weak - * topology are locally convex spaces that are important in the theory of normalized spaces.
• Different operator topologies lead to locally convex spaces in the theory of operator algebras .

literature

• J. Dieudonné : History of Functional Analysis , North-Holland Mathematical Studies 49 (1981), ISBN 0-444-86148-3
• G. Köthe : Topological Vector Spaces I (2nd edition), Springer, 1983, ISBN 3-540-04509-0
• G. Köthe: Topological Vector Spaces II , Springer, 1979, ISBN 3-540-90400-X
• K. Floret, J. Wloka : Introduction to the theory of locally convex spaces , Lecture Notes in Mathematics 56, 1968, ISBN 3-540-04226-1
• HH Schaefer: Topological Vector Spaces , Springer, 1971 ISBN 0-387-98726-6
• H. Jarchow: Locally Convex Spaces , Teubner, Stuttgart 1981 ISBN 3-519-02224-9
• R. Meise, D. Vogt: Introduction to Functional Analysis , Vieweg, 1992 ISBN 3-528-07262-8
• J. v. Neumann : On Complete Topological Spaces , Transactions of the American Mathematical Society 37 (1935), pp. 1-20

Individual evidence

1. ^ R. Meise, D. Vogt: Introduction to Functional Analysis , Vieweg, 1992 ISBN 3-528-07262-8 , Lemma 22.2