Convolution (math)
In functional analysis , a sub-area of mathematics , the convolution , also called convolution (from the Latin convolvere "to roll up"), describes a mathematical operator that provides two functions and a third function .
The convolution clearly means that each value of is replaced by the weighted mean of the values surrounding it. More specifically, for the average value of the function value with weighted. The resulting “overlay” between and mirrored and shifted versions of (one also speaks of a “smear” of ) can e.g. B. can be used to form a moving average .
definition
Convolution for functions
The convolution of two functions is defined by
In order to keep the definition as general as possible, one does not restrict the space of the admissible functions at first and instead demands that the integral for almost all values of is well-defined.
In the case , i.e. for two integrable functions (in particular this means that the improper absolute value integral is finite), one can show that this requirement is always fulfilled .
Convolution of periodic functions
For periodic functions and a real variable with a period , the convolution is defined as
- ,
whereby the integration extends over any interval with period length . It is again a periodic function with period .
Convolution for functions on intervals
In the case of a limited domain , one continues and to the entire space in order to be able to carry out the convolution. There are several approaches to this, depending on the application.
- Continuation through zero
- It returns the functions by definition outside of the domain by the null function continued .
- Periodic continuation
- The functions are periodically continued outside the domain and the convolution defined for periodic functions is used.
In general, the convolution for such continued functions is no longer well-defined. An exception that often occurs is continuous functions with a compact carrier , which can be continued through zero to form an integrable function in .
meaning
A clear interpretation of the one-dimensional convolution is the weighting of one function that is dependent on time with another. The function value of the weight function at one point indicates how strong the order past , so the weighted value function in the value of the result function at the time arrives.
Convolution is a suitable model for describing numerous physical processes.
Smoothing core

One way to " smooth out " a function is to fold it with something called a smooth core. The resulting function is smooth (infinitely often continuously differentiable), its support is only slightly larger than that of , and the deviation in the L1 norm can be limited by a given positive constant.
A -dimensional smoothing kernel or Mollifier is an infinitely often continuously differentiable function , which is nonnegative, has its carrier in the closed unit sphere and has the integral 1, through the appropriate choice of a constant .
One example is the smoothing kernel
where is a normalization constant.
This function can be used to create further smoothing cores by setting for :
- where for .
Examples
Rectangular function
Be
- .
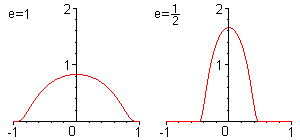
By folding (shown in red) to the smoothing kernel is a smooth function is created (shown in blue) with compact support, of f in L 1 - standard deviates by about 0.4, d. H.
- .
When convolution with for e less than 1/2 one obtains smooth functions which are even closer to f in the integral norm .
Normal distribution
If a normal distribution with the mean value and the standard deviation is convoluted with a second normal distribution with the parameters and , a normal distribution with the mean value and the standard deviation results again .
| proof |
|---|
|
|
This is how the Gaussian error addition can be justified: Given are two bars with error-prone lengths and . If you want to know how long the assembled rod is, then you can consider the two rods as a randomly distributed ensemble. It can e.g. B. be that rod 1 is really long. This event occurs with a certain probability, which can be read from the normal distribution . For this event, the total length of the two bars is normally distributed, namely with the normal distribution of the 2nd bar multiplied by the probability that the 1st bar is long. If one goes through this for all member lengths for member 1 and adds the distributions of the composite member, then this corresponds to the integration given in the proof, which is equivalent to a convolution. The composite rod is therefore also normally distributed and long.
Properties of the fold
Algebraic properties
The convolution of -functions together with the addition satisfies almost all axioms of a commutative ring, with the exception that this structure has no neutral element . One speaks jokingly of an "Rng" because the i for "identity" is missing. In detail, the following properties apply:
- Associativity with scalar multiplication
- Where is any complex number .
Derivation rule
It is the distributional derivative of . If (totally) differentiable, the distributional derivation and (total) derivation agree. Two interesting examples are:
- , where is the derivative of the delta distribution . The derivation can therefore be understood as a convolution operator.
- , where is the step function, gives an antiderivative for .
integration
If and are integrable functions, then applies
This is a simple consequence of Fubini's theorem .
Convolution theorem
Using the Fourier transform
one can express the convolution of two functions as the product of their Fourier transforms:
A similar theorem also applies to the Laplace transformation . The reverse of the convolution theorem says:
It is the point by point product of the two functions is thus equivalent to at any point .
Reflection operator
Let it be the reflection operator with for all , then applies
- and
Convolution of dual L p functions is continuous
Be and with and . Then the convolution is a bounded continuous function on . If , the convolution disappears at infinity, so it is a function . This statement is also correct if is a real Hardy function and lies in BMO .
Generalized Young's inequality
The generalized Young 's inequality follows from Hölder's inequality
for and .
Convolution as an integral operator
Let , then the convolution can also be understood as an integral operator with the integral kernel. That is, one can define the convolution as an operator
grasp. This is a linear and compact operator that is also normal . Its adjoint operator is given by
Also is a Hilbert-Schmidt operator .
Discrete folding
In digital signal processing and digital image processing , one usually has to deal with discrete functions that need to be folded together. In this case a sum takes the place of the integral and one speaks of the time-discrete convolution.
definition
Let be functions with the discrete domain . Then the discrete convolution is defined by
- .
The summation range is the entire definition range of both functions. In the case of a limited domain, and are usually continued with zeros.
If the domain is finite, the two functions can also be understood as vectors , respectively . The convolution is then given as a matrix-vector product :
with the matrix
with and
If you continue the columns from below and above the periodically, instead of adding zeros , you get a cyclic matrix , and you get the cyclic convolution .
Applications
The product of two polynomials and is, for example, the discrete convolution of their coefficient sequences continued with zeros. The infinite series that occur thereby always only have a finite number of summands that are not equal to zero. The product of two formal Laurent series with a finite main part is defined analogously .
An algorithm for calculating the discrete convolution that is efficient in terms of computing power is the fast convolution , which in turn is based on the fast Fourier transform (FFT) for the efficient computation of the discrete Fourier transform.
Distributions
The convolution was extended to distributions by Laurent Schwartz , who is considered the founder of distribution theory .
Folding with one function
Another generalization is the convolution of a distribution with a function . This is defined by
where is a translation and reflection operator defined by .
Convolution of two distributions
Be and two distributions, one having a compact carrier. Then for all the convolution between these distributions is defined by
- .
A further statement ensures that there is a clear distribution with
for everyone .
Algebraic properties
Be , and distributions, then applies
- Associativity with scalar multiplication
- Where is any complex number .
-
Neutral element
- , where is the delta distribution .
Convolution theorem
With is the Fourier transform described by distributions. Now be a tempered distribution and a distribution with a compact carrier. Then it is and it applies
- .
Topological groups
Convolution on topological groups
The two convolution terms can be described and generalized together by a general convolution term for complex-valued m -integratable functions on a suitable topological group G with a measure m (e.g. a locally compact Hausdorff topological group with a Haar measure ):
This concept of convolution plays a central role in the representation theory of these groups, the most important representatives of which are the Lie groups . The algebra of the integrable functions with the convolution product is for compact groups the analogue of the group ring of a finite group. Further topics are:
The folding algebra of finite groups
For a finite group with the amount of addition and scalar multiplication is a vector space, isomorphic to The folding
is then an algebra , called the convolution algebra .
Convolutional algebra has a base indexed with the group elements where
The following applies to the convolution:
We define a mapping between and by defining for base elements: and continue linearly. This mapping is obviously bijective . It is seen from the above equation for the convolution of two basic elements of the multiplication in the in equivalent. Thus the convolutionalgebra and the group algebra are isomorphic as algebras.
With the involution it becomes an algebra . It is
an illustration of a group goes to a -Algebrenhomomorphismus by
Da as -Algebrenhomomorphismus particular multiplicative, we obtain If unitary is furthermore apply the definition of a unitary account is given in Chapter properties . There it is also shown that we can assume a linear representation to be unitary without restriction.
Within the framework of convolution algebra, a Fourier transformation can be carried out on groups . In the harmonic analysis it is shown that this definition is consistent with the definition of the Fourier transform .
If a representation, then the Fourier transform is defined by the formula
It then applies
application
- In optics , a wide variety of image disturbances can be modeled as a convolution of the original image with a corresponding core. In digital image processing , convolution is therefore used to simulate such effects. Other digital effects are also based on the convolution. When determining the direction of image edges , 3 × 3 and 5 × 5 folds are essential.
- In the case of a linear, time-invariant transmission element , the response to an excitation is obtained by convolution of the excitation function with the impulse response of the transmission element. For example, the linear filtering of an electronic signal represents the convolution of the original function with the impulse response.
- Convolution is used to construct special solutions of certain partial differential equations . Is the fundamental solution of the partial differential operator , then a solution of partial differential equation .
- Diffusion processes can be described by folding.
- If and are two stochastically independent random variables with probability densities and , then the density of the sum is equal to the convolution .
- In acoustics (music), convolution (with the aid of FFT = fast Fourier transform ) is also used to digitally generate reverbs and echoes and to adapt sound properties. To do this, the impulse response of the room whose sound characteristics you want to adopt is folded with the signal you want to influence.
- In engineering mathematics and signal processing, input signals (external influences) are convoluted with the impulse response (reaction of the system under consideration to a Dirac impulse as a signal input, also weight function) in order to calculate the response of an LTI system to any input signals. The impulse response should not be confused with the step response . The former describes the entirety of the system and a Dirac pulse as an input test function, the latter the entirety of the system and a step function as an input test function. The calculations usually do not take place in the time domain, but in the frequency domain. For this purpose, both the signal and the impulse response describing the system behavior must be present in the frequency domain or, if necessary, transformed from the time domain by Fourier transformation or one-sided Laplace transformation. The corresponding spectral function of the impulse response is called the frequency response or transfer function.
- In numerical mathematics , the B- spline basis function for the vector space of piecewise polynomials of degree k is obtained by convolution of the box function with .
- In computer algebra , the convolution can be used for an efficient calculation of the multiplication of multi-digit numbers, since the multiplication essentially represents a convolution with a subsequent carry. The complexity of this procedure is almost linear, while the “school procedure” has a quadratic effort , where the number of positions is. This is worthwhile despite the additional effort required for the Fourier transformation (and its inversion).
- In hydrology , convolution is used to calculate the runoff produced by a precipitation runoff event in a catchment area with a given amount and duration of precipitation. For this purpose, the so-called "unit hydrograph" (unit discharge hydrograph ) - the discharge hydrograph on a unit precipitation of a given duration - is folded with the temporal function of the precipitation.
- In reflection seismics , a seismic trace is viewed as a convolution of impedance contrasts of the geological layer boundaries and the output signal (wavelet). The process of restoring the undistorted layer boundaries in the seismogram is deconvolution .
literature
- N. Bourbaki: Integration. Springer, Berlin a. a. 2004, ISBN 3-540-41129-1 .
- Kôsaku Yosida: Functional Analysis . Springer-Verlag, Berlin a. a. 1995, ISBN 3-540-58654-7 .
References and footnotes
- ↑ More generally it can also be assumed for a and . See Herbert Amann, Joachim Escher: Analysis III . 1st edition. Birkhäuser-Verlag, Basel / Boston / Berlin 2001, ISBN 3-7643-6613-3 , section 7.1.
- ^ Proof by inserting the inverse Fourier transform. E.g. as in Fourier transform for pedestrians, Tilman Butz, Edition 7, Springer DE, 2011, ISBN 978-3-8348-8295-0 , p. 53, Google Books
- ↑ ( page no longer available , search in web archives: dt.e-technik.uni-dortmund.de ) (PDF).
- ↑ Dirk Werner : Functional Analysis . 6th, corrected edition, Springer-Verlag, Berlin 2007, ISBN 978-3-540-72533-6 , p. 447.





























![{\ displaystyle c = \ left [\ int _ {B (0,1)} \ exp \! \ left (- {\ frac {1} {1- | x | ^ {2}}} \ right) dx \ right] ^ {- 1} <\ infty}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d363a67c6ce79e245c93d80ecb02abc39e7d6b)
![e \ in (0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c0822498a98441e945ce4254df5387b4643025a)


















![{\ displaystyle = {\ frac {1} {2 \ pi \ sigma _ {1} \ sigma _ {2}}} e ^ {- {\ frac {\ mu _ {1} ^ {2} \ sigma _ { 2} ^ {2} + (x- \ mu _ {2}) ^ {2} \ sigma _ {1} ^ {2}} {2 \ sigma _ {1} ^ {2} \ sigma _ {2} ^ {2}}}} \ int \ limits _ {- \ infty} ^ {\ infty} e ^ {- {\ frac {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2 }} {2 \ sigma _ {1} ^ {2} \ sigma _ {2} ^ {2}}} \ left [\ left (\ mathbf {\ xi} - {\ frac {\ mu _ {1} \ sigma _ {2} ^ {2} + (x- \ mu _ {2}) \ sigma _ {1} ^ {2}} {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2}}} \ right) ^ {2} - \ left ({\ frac {\ mu _ {1} \ sigma _ {2} ^ {2} + (x- \ mu _ {2}) \ sigma _ {1} ^ {2}} {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2}}} \ right) ^ {2} \ right]} \ mathbf {\ mathrm {d } \ xi}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab3c2a4cd0f41e09c9e773153511d1f635b4d6c4)



![{\ displaystyle = {\ underline {\ underline {{\ frac {1} {{\ sqrt {2 \ pi}} {\ sqrt {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ { 2}}}}} e ^ {- {\ frac {\ left [x - (\ mu _ {1} + \ mu _ {2}) \ right] ^ {2}} {2 {\ sqrt {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2}}} ^ {2}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86a284cdbe033c886c1e112d6775c72ca5909c1)






































![h \ in L ^ {2} ([0.2 \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d0c96e5290b307064035669a7afc89d7c358879)

![T_ {h} \ colon L ^ {2} ([0.2 \ pi]) \ to L ^ {2} ([0.2 \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9972247fc27b5ade890c70e37470221e01d46c7)
![T_ {h} f (s): = {\ frac {1} {2 \ pi}} \ int _ {{[0,2 \ pi]}} f (t) h (st) {\ mathrm {d} } t](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfe47dd77521e52b81383fbece7a9cfe9d49d48d)
![T_ {h} ^ {*} f (s) = {\ frac {1} {2 \ pi}} \ int _ {{[0,2 \ pi]}} f (t) \ overline {h (ts) } {\ mathrm {d}} t \ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a9997004f3f0a2ba0bed4ed25373893af481ed)













































![{\ displaystyle \ mathbb {C} [G],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc160488569e6cb6a4978e1e3ccf18766ed0835d)


![{\ displaystyle \ mathbb {C} [G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72c0617967677acd130f2710308f9d00a288efc5)




























![p \ in [1; \ infty]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c52af51a5360de86a7c96c4986a07b6c615fab45)
