Laplace transform

The Laplace transformation , named after Pierre-Simon Laplace , is a one-sided integral transformation that converts a given function from the real time domain to a function in the complex spectral domain ( frequency domain ; image domain ). This function is called the Laplace transform or spectral function. ${\displaystyle f}$ ${\displaystyle F}$ ${\displaystyle F}$

The Laplace transformation has similarities with the Fourier transformation : There is also an inverse transformation for the Laplace transformation, which is also called the Bromwich integral .

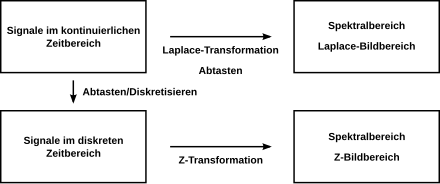
The Laplace transform applies to signals in the continuous time domain. It is related to a corresponding transformation for signals in the discrete time domain: the Z transformation .

Comparison of the Z transform and the Laplace transform

General

The Laplace transformation and its inversion are methods for solving problems in mathematical physics and theoretical electrical engineering, which are mathematically described by linear initial and boundary value problems . The Laplace transformation belongs to the class of functional transformations , more specifically to the integral transformations , and is closely related to the Fourier transformation . The motivation to further develop the Fourier transform into the Laplace transform lies in the restricted class of functions for which the Fourier integral exists in the context of the Fourier transform.

In order to ensure convergence for a larger range of functions in the Laplace transform, the integration of the Fourier integral is extended by the factor that goes for σ> 0 and towards 0 and thus ensures convergence for sufficiently large t. The frequency parameter of the Fourier transformation is thus transformed into the complex frequency parameter. ( is the imaginary unit with . In electrical engineering, instead of is used because it stands for the alternating electrical current.) In contrast to the two-sided Laplace transform and also the Fourier transform, the usual, one-sided Laplace transform is only for positive values ​​of t ≥ 0 is defined. This restriction is permissible because in the context of systems theory and application in the field of physics and technology, only actually existing causal systems play a role. The two-sided Laplace transformation is necessary for the theoretical investigation of non-causal systems. ${\displaystyle e^{-\sigma t},\sigma \in \mathbb {R} }$ ${\displaystyle t\to \infty }$ ${\displaystyle \mathrm {i} \omega }$ ${\displaystyle s=\sigma +\mathrm {i} \omega }$ ${\displaystyle \mathrm {i} }$ ${\displaystyle \mathrm {i} ^{2}=-1}$ ${\displaystyle \mathrm {j} }$ ${\displaystyle \mathrm {i} }$ ${\displaystyle \mathrm {i} }$

The Laplace transformation maps original functions of a real variable onto image functions of a complex variable. If the Laplace transformation exists, the differentiation and integration in the real original domain corresponds to a simple algebraic operation in the image domain, which is the reason for its practical significance. In the case of many initial and boundary value problems, the time domain plays the role of the real original domain and the frequency domain or spectral domain that of the complex image domain.

The investigation of the image function often provides much better physical insights into the behavior of linear systems compared to studies in the time domain. In particular, the resonance behavior of physical systems can be described more easily in the frequency domain. Due to the better convergence compared to the Fourier transformation, for example, transfer functions can still be analyzed even if a linear system is unstable.

In the case of time-discrete systems, in order to avoid the periodicity in the s-plane (this is due to the temporally discrete sampling values ​​in the context of the discrete Laplace transformation), a conformal, non-linear mapping is carried out on the so-called z-plane, which leads to the Z- Transformation leads.

history

The first references to the idea of ​​the Laplace transformation can be found in the work of the Basel mathematician and physicist Leonhard Euler (1707–1783, Institutiones calculi integralis, vol. 2, 1768). The Laplace transformation is named after the French mathematician and astronomer Pierre-Simon Laplace (1749–1827), who introduced the transformation in 1782 as part of probability studies. In fact, the Hungarian mathematician József Miksa Petzval (1807-1891) was the first to study it systematically, whereas Laplace used it only to solve his problems. However, Petzval's work received no attention, among other things because one of his students had wrongly accused him of plagiarism against Laplace.

About a hundred years later, the British electrical engineer and physicist Oliver Heaviside (1850–1925) applied the operator calculus he had found through trial and error to solve differential equations in theoretical electrical engineering. The German mathematician Gustav Doetsch (1892–1977) replaced this with the Laplace transformation, developed its mathematical foundations and introduced the Laplace transformation to a wide range of applications for solving many problems in mathematical physics and theoretical electrical engineering Boundary value problems are described. Since at least the early 1960s, the theory and application of the Laplace transformation have been found in textbooks and curricula in theoretical electrical engineering, and above all in books on ordinary and partial differential equations.

The Polish mathematician Jan Mikusiński (1913–1987) carried out a purely algebraic justification and expansion of the Heaviside operator calculation without using the Laplace transformation. This extension also covers functions that do not have a Laplace transform and, for example, provides a simple, exact justification for the delta function without using distributions .

definition

Be a function. The Laplace transform of is through ${\displaystyle f\colon {[0,\infty [}\rightarrow \mathbb {C} }$ ${\displaystyle f(t)}$

${\displaystyle F(s)={\mathcal {L}}\left\{f\right\}(s)=\int _{0}^{\infty }f(t)e^{-st}\,\mathrm {d} t,\qquad s\in \mathbb {C} }$

defined insofar as the integral exists. It is an ( improper ) parameter integral with the parameter . The exponential function is the core of the Laplace transform. The function is called the Laplace transform of the function . ${\displaystyle s}$ ${\displaystyle \mathrm {e} ^{-st}}$ ${\displaystyle F(s)}$ ${\displaystyle f(t)}$

existence

A function is said to be of exponential order if there are constants , with , and a digit with such that ${\displaystyle f\colon {[0,\,\infty [}\rightarrow \mathbb {C} }$ ${\displaystyle C}$ ${\displaystyle s_{0}}$ ${\displaystyle C>0}$ ${\displaystyle s_{0}>0}$ ${\displaystyle T}$ ${\displaystyle T>0}$

${\displaystyle |f(t)|\leq Ce^{s_{0}t}}$     For     ${\displaystyle t>T}$

applies. Sometimes the stricter condition is used instead . ${\displaystyle t>0}$ ${\displaystyle t>T}$

If is of exponential order, and thus the sizes , , are given from the above equation, and when, in addition ${\displaystyle f}$ ${\displaystyle C}$ ${\displaystyle s_{0}}$ ${\displaystyle T}$

${\displaystyle \int _{0}^{T}|f(t)|\,\mathrm {d} t<\infty }$

holds, then the Laplace integral exists in the half-plane . ${\displaystyle \operatorname {Re} (s)>s_{0}}$ ${\displaystyle {\mathcal {L}}\{f\}(s)}$

The condition is met if the function in continuous piecewise is. ${\displaystyle \textstyle \int _{0}^{T}|f(t)|\,\mathrm {d} t<\infty }$ ${\displaystyle f}$ ${\displaystyle [0,\,\infty [}$

Examples of functions whose Laplace integral exists are listed in the correspondence tables below.

The mentioned conditions are only sufficient for the existence of the Laplace integral. If they are not met, further investigation must be made.

Some examples:

• The function is indeed of exponential order (you sit , , ), but not piecewise continuous, and the integral in (2) for each divergent. This function has no Laplace transform. ${\displaystyle {\tfrac {1}{t}}}$ ${\displaystyle C=1}$ ${\displaystyle T=1}$ ${\displaystyle s_{0}=1}$ ${\displaystyle [0,\,\infty [}$ ${\displaystyle T}$
• The function is not of exponential order and has no Laplace transform either. ${\displaystyle e^{t^{2}}}$
• The function is , however, not piecewise exponential order of (insert , , ), also the integral exists (the value ). The Laplace integral exists and is equal . ${\displaystyle {\tfrac {1}{\sqrt {t}}}}$ ${\displaystyle [0,\,\infty [}$ ${\displaystyle C=1}$ ${\displaystyle T=1}$ ${\displaystyle s_{0}=1}$ ${\displaystyle \textstyle \int _{0}^{T}|f(t)|\,\mathrm {d} t}$ ${\displaystyle 2{\sqrt {T}}}$ ${\displaystyle \textstyle {\sqrt {\tfrac {\pi }{s}}}}$

Laplace inverse transform

For the Laplace transformation there is also an inverse transformation, i.e. an operator that assigns the corresponding time function to a given spectral function . This integral operator is also called the Bromwich integral and is named after the mathematician and physicist Thomas John I'Anson Bromwich . ${\displaystyle F(s)}$ ${\displaystyle f(t)}$

statement

The time function can be given by the inverse formula ${\displaystyle f(t)}$

${\displaystyle {\mathcal {L}}^{-1}\left\{F(s)\right\}={\frac {1}{2\pi \mathrm {i} }}\int _{\gamma -\mathrm {i} \infty }^{\gamma +\mathrm {i} \infty }e^{st}F(s)\,\mathrm {d} s={\begin{cases}f(t)&{\text{für }}t\geq 0\\0&{\text{für }}t<0\end{cases}}\qquad {\text{mit }}\gamma >s_{0},}$

can be determined from the spectral function, where the greatest real part of a singularity is . ${\displaystyle F(s)}$ ${\displaystyle s_{0}}$ ${\displaystyle F}$

example

Known inverse transformations are summarized in the literature in correspondence tables. In practice, therefore, the spectral function usually only has to be traced back to these tabulated cases, e.g. B. by partial fraction decomposition .

As an example, consider the inverse transformation of fractional rational functions: For the spectral function

${\displaystyle F(s)=\sum _{k=1}^{n}{\frac {\alpha _{k}}{s-s_{k}}}}$

can be done with the (tabulated, here exemplarily calculated) correspondence

${\displaystyle {\mathcal {L}}\{e^{at}\}=\int _{0}^{\infty }e^{at}\ e^{-st}\,\mathrm {d} t=\left.{\frac {e^{(a-s)t}}{a-s}}\right|_{0}^{\infty }={\frac {1}{s-a}}}$

Specify the inverse transformed directly as

${\displaystyle f(t)=\sum _{k=1}^{n}\alpha _{k}e^{s_{k}t}}$

In the case of complex conjugate poles, simplifications are possible by using trigonometric identities. ${\displaystyle f(t)}$

Important applications

In general, the Laplace transformation is suitable for solving linear differential equations or differential equation systems with constant coefficients. The advantage here is the algebraization: derivatives in the image area arise as the product of the Laplace transform of the original function and the Laplace factor . This causes ${\displaystyle s}$

• ordinary differential equations in the original area to algebraic equations in the image area,
• partial differential equations with independent variables in the original area to partial (or ordinary) differential equations with independent variables in the image area, ${\displaystyle n}$ ${\displaystyle n-1}$
• and convolution-type integral equations in the original area to algebraic equations in the image area

be mapped. The solutions to the transformed problems can be worked out much more easily in the image area than in the original area. In special cases, linear differential equations with polynomial coefficients can also be solved in this way.

The Laplace transformation is particularly efficient for solving initial value problems, since the initial values ​​are included in the image equation. The differential equation is transformed into the spectral domain , the algebraic equation thus obtained is solved and the solution is transformed back into the time domain . At this point it should be pointed out once again that the result obtained only provides information for the period ab , since the Laplace transform is determined by the integration ab . ${\displaystyle t=0}$ ${\displaystyle t=0}$

The disadvantage is the generally complicated inverse transformation.

In mechanical engineering and electrical engineering , especially in control engineering , the Laplace transformation plays a major role , primarily because of the convolution theorem . Since the behavior of the system output can be represented in the spectral range as the product of the input function and a transfer function specific to the system and independent of the respective excitation , many system properties can be determined by examining the transfer function (which in turn is obtained by simply combining elementary transfer functions) without a to determine an explicit solution of the system differential equation, for example by inverse transformation. This elegantly enables, for example, the stability analysis of linear time-invariant systems and analysis of the vibration behavior (damping), the speed of both controlled systems and closed control loops. Since the transfer function in the Laplace range changes into a transfer function in the Fourier range, graphical representations of the transfer behavior, i.e. amplitude and phase frequency responses ( Bode diagrams ) can also be obtained. ${\displaystyle s=j\omega }$

properties

Limit sets

${\displaystyle \lim _{s\to 0+}sF(s)=\lim _{t\to \infty }f(t)}$

${\displaystyle \lim _{s\to \infty }sF(s)=\lim _{t\to 0+}f(t)}$

In particular, each Laplace transform tends to when to aims. The first limit theorem only applies if apart from a single pole, there are no singularities in the half-plane . ${\displaystyle 0}$ ${\displaystyle \operatorname {Re} s}$ ${\displaystyle +\infty }$ ${\displaystyle F(s)}$ ${\displaystyle s=0}$ ${\displaystyle \operatorname {Re} s\geq 0}$

Uniqueness

If for two time functions and the prerequisites apply: ${\displaystyle f(t)}$ ${\displaystyle g(t)}$

• ${\displaystyle f(t)}$and are piecewise continuous ${\displaystyle g(t)}$
• ${\displaystyle f(t)}$and are of exponential order for ${\displaystyle g(t)}$ ${\displaystyle t\to \infty }$
• the Laplace transforms and exist ${\displaystyle F(s)={\mathcal {L}}\{f(t)\}}$ ${\displaystyle G(s)={\mathcal {L}}\{g(t)\}}$
• ${\displaystyle F(s)=G(s)}$ in the convergence area

then is everywhere where and are steady. ${\displaystyle f(t)=g(t)}$ ${\displaystyle f}$ ${\displaystyle g}$

Compare: Lerch's uniqueness theorem

Relationship to the Fourier transform

The Laplace transform is an integral transform similar to the Fourier transform . If one sets with real , the special case arises ${\displaystyle s=\mathrm {i} \omega }$ ${\displaystyle \omega \in \mathbb {R} }$

${\displaystyle {\mathcal {F}}_{\infty }(f)(\omega )={\mathcal {L}}(f)(\mathrm {i} \omega )=\int _{0}^{\infty }\mathrm {e} ^{-\mathrm {i} \omega t}f(t)\,\mathrm {d} t.}$

This integral transformation is sometimes called a one-sided Fourier transform.

Analytical properties

Analyticity

The Laplace transform is in the image area due to the existence of its derivatives according to the complex frequency ${\displaystyle s}$

${\displaystyle F^{(n)}(s)={\mathcal {L}}\{(-t)^{n}f(t)\}\qquad (n=1,2,3,\dots )}$

within the convergence half-level, complex differentiable as often as desired, that is, analytically (or regular or holomorphic ). Thus, it is possible to investigate with the means of function theory. The function can be analytically continued in the left half-plane, but not mandatory. Such an analytical continuation can then no longer be written as a Laplace transform. ${\displaystyle F(s)}$ ${\displaystyle F(s)}$

Conjugated Symmetry

Another important property of the Laplace transform of real time functions is the conjugate symmetry in the complex image domain

${\displaystyle F({\bar {s}})={\bar {F}}(s)}$

or separated into real and imaginary parts

${\displaystyle \operatorname {Re} (F({\bar {s}}))=\operatorname {Re} (F(s))}$

${\displaystyle \operatorname {Im} (F({\bar {s}}))=-\operatorname {Im} (F(s))}$

where the overline denotes the complex conjugate quantity. Because of this property, it is sufficient to study the image function in the upper half-plane . ${\displaystyle \operatorname {Im} (s)\geq 0}$

Finite Laplace Transform

The Laplace transform forms a finite time function

${\displaystyle f(t)=0}$ For ${\displaystyle {\begin{cases}t<0\\t>T\end{cases}}}$

on a whole function . This means that the picture function

${\displaystyle F(s)=\int _{0}^{T}f(t)e^{-st}\,\mathrm {d} t}$

is analytical in the entire complex frequency plane, i.e. has no singularities .

Physical dimension

In applications of the Laplace transform, the dimension is also the Laplace transform

${\displaystyle F(s)={\mathcal {L}}\left\{f(t)\right\}=\int _{0}^{\infty }e^{-st}f(t)\,\mathrm {d} t\qquad ({\textrm {mit:}}\quad s=\sigma +\mathrm {i} \omega ;\quad \sigma >0;\quad t\geq 0)}$

of interest. The complex frequency has the dimension . The expression in the integrand is therefore dimensionless. By integrating over the time domain, the dimension of the time function is multiplied by the dimension of the time differential : ${\displaystyle s}$ ${\displaystyle \mathrm {Zeit} ^{-1}}$ ${\displaystyle e^{-st}}$ ${\displaystyle f(t)}$ ${\displaystyle \mathrm {d} t}$

${\displaystyle [F(s)]=[f(t)][t]=[f(t)]s}$.

For example, the Laplace transform of an electrical current (measured in amperes ) ${\displaystyle i(t)}$

${\displaystyle I(s)={\mathcal {L}}\left\{i(t)\right\}=\int _{0}^{\infty }e^{-st}i(t)\,\mathrm {d} t}$

the dimension of a charge As = C, i.e. coulomb .

Correspondence tables

General properties

General property or operation	Original function ${\displaystyle f(t)={\mathcal {L}}^{-1}\left\{F(s)\right\}}$	Image function ${\displaystyle F(s)={\mathcal {L}}\left\{f(t)\right\}}$
Linearity	${\displaystyle a_{1}f_{1}(t)+a_{2}f_{2}(t)\,}$	${\displaystyle a_{1}F_{1}(s)+a_{2}F_{2}(s)\,}$
Similarity theorem	${\displaystyle f(at)\,}$	${\displaystyle {\frac {1}{a}}F\left({\frac {s}{a}}\right)\qquad (a>0)\,}$
Shift in the original area (with one-sided transformation only or ) ${\displaystyle a>0\,}$ ${\displaystyle f(t)=0\,}$ ${\displaystyle \forall \,}$ ${\displaystyle t<a\,}$	${\displaystyle f(t-a)\,}$	${\displaystyle e^{-as}F(s)\,}$
Shift in the image area (damping theorem)	${\displaystyle e^{-at}\cdot f(t)\,}$	${\displaystyle F(s+a)\qquad (a\in \mathbb {C} )\,}$
Complex conjugation	${\displaystyle f^{*}(t)\,}$	${\displaystyle F^{*}(s^{*})\,}$
Time mirroring (not applicable for one-sided transformation!)	${\displaystyle f(-t)\,}$	${\displaystyle F(-s)\,}$
Time expansion ( with one-sided transformation only for ) ${\displaystyle T\neq 0}$ ${\displaystyle T>0}$	${\displaystyle f\left({\frac {t}{T}}\right)\,}$	${\displaystyle |T|F(s\cdot T)\,}$
Sin multiplication	${\displaystyle \sin(at)\cdot f(t)\,}$	${\displaystyle {\frac {1}{2\mathrm {i} }}\cdot (F(s-\mathrm {i} a)-F(s+\mathrm {i} a))}$
Cosine multiplication	${\displaystyle \cos(at)\cdot f(t)\,}$	${\displaystyle {\frac {1}{2}}\cdot (F(s-\mathrm {i} a)+F(s+\mathrm {i} a))}$
	${\displaystyle \sinh(at)\cdot f(t)\,}$	${\displaystyle {\frac {1}{2}}\cdot (F(s-a)-F(s+a))}$
	${\displaystyle \cosh(at)\cdot f(t)\,}$	${\displaystyle {\frac {1}{2}}\cdot (F(s-a)+F(s+a))}$
1. Derivation in the original area	${\displaystyle f'(t)\,}$	${\displaystyle sF(s)-f(0)\,}$
2. Derivation in the original area	${\displaystyle f''(t)\,}$	${\displaystyle s^{2}F(s)-sf(0)-f'(0)\,}$
${\displaystyle n^{te}}$ Derivation in the original area	${\displaystyle f^{(n)}(t)\,}$	${\displaystyle s^{n}F(s)-\sum _{k=0}^{n-1}f^{(k)}(0)s^{n-k-1}\,}$
1. Derivation in the image area	${\displaystyle -tf(t)\,}$	${\displaystyle F^{\prime }(s)\,}$
2. Derivation in the image area	${\displaystyle t^{2}f(t)\,}$	${\displaystyle F^{\prime \prime }(s)\,}$
${\displaystyle n^{te}}$ Derivation in the image area	${\displaystyle (-t)^{n}f(t)\,}$	${\displaystyle F^{(n)}(s)\,}$
Integration in the original area	${\displaystyle \int _{0}^{t}f(u)\,\mathrm {d} u}$ ${\displaystyle {\frac {1}{(n-1)!}}\int _{0}^{t}(t-q)^{n-1}f(q)\,\mathrm {d} q,\,\,n\geq 1}$	${\displaystyle {\frac {1}{s}}F(s)}$ ${\displaystyle {\frac {1}{s^{n}}}F(s),\,\,n\geq 1}$
Integration in the image area	${\displaystyle {\frac {1}{t}}f(t)}$	${\displaystyle \int _{s}^{\infty }F(u)\,\mathrm {d} u}$
Convolution in the original area. Multiplication in the image area	${\displaystyle \int _{0}^{t}f(u)\,g(t-u)\,\mathrm {d} u}$	${\displaystyle F(s)\,G(s)}$
Multiplication in the original area Convolution in the image area	${\displaystyle f(t)\,g(t)}$	${\displaystyle {\frac {1}{2\pi \mathrm {i} }}\int _{c-\mathrm {i} \infty }^{c+\mathrm {i} \infty }F(\sigma )\,G(s-\sigma )\,\mathrm {d} \sigma }$ converges for where is greater than the pole of G with the greatest real part. ${\displaystyle Re(s-\sigma )>\sigma _{G}}$ ${\displaystyle \sigma _{G}}$
Periodic function	${\displaystyle f(t)=f(t+T)\,}$	${\displaystyle {\frac {1}{1-e^{-sT}}}\int _{0}^{T}f(t)\cdot e^{-st}\,\mathrm {d} t}$

Correspondence table

The following applies to the original function . ${\displaystyle f(t)=0\quad \forall \;t<0}$

Function name	Original function ${\displaystyle f(t)={\mathcal {L}}^{-1}\left\{F(s)\right\}}$	Image function ${\displaystyle F(s)={\mathcal {L}}\left\{f(t)\right\}}$	Convergence - range
Dirac delta distribution Unit momentum	${\displaystyle \delta (t)\,}$ ${\displaystyle {\frac {\mathrm {d} ^{n}}{\mathrm {d} t^{n}}}\delta (t)\,}$	${\displaystyle 1\,}$ ${\displaystyle s^{n}\,}$	${\displaystyle s\in \mathbb {C} \,}$
Heaviside step function unit jump	${\displaystyle \Theta (t)\,}$	${\displaystyle {\frac {1}{s}}}$	${\displaystyle \operatorname {Re} (s)>0}$
Exponential function	${\displaystyle e^{-at}\,}$	${\displaystyle {\frac {1}{s+a}}}$	${\displaystyle \operatorname {Re} (s)>-a}$
Exponential distribution	${\displaystyle 1-e^{-at}\,}$	${\displaystyle {\frac {a}{s(s+a)}}}$	${\displaystyle \operatorname {Re} (s)>-a}$
1st power	${\displaystyle t\ }$	${\displaystyle {\frac {1}{s^{2}}}}$	${\displaystyle \operatorname {Re} (s)>0}$
nth power	${\displaystyle t^{n}\,}$	${\displaystyle {n! \over s^{n+1}}}$	${\displaystyle \operatorname {Re} (s)>0}$
Power series	${\displaystyle \sum _{n=0}^{\infty }a_{n}(t-t_{0})^{n}\,}$	${\displaystyle \sum _{n=0}^{\infty }{\frac {a_{n}n!}{s^{n+1}}}e^{-t_{0}s}}$	${\displaystyle \operatorname {Re} (s)>0}$
Damped power function	${\displaystyle te^{-at}\,}$	${\displaystyle {\frac {1}{(s+a)^{2}}}}$	${\displaystyle \operatorname {Re} (s)>-a}$
	${\displaystyle t^{n}e^{-at}\,}$	${\displaystyle {\frac {n!}{(s+a)^{n+1}}}}$	${\displaystyle \operatorname {Re} (s)>-a}$
	${\displaystyle {\frac {t^{n-1}}{(n-1)!}}\cdot e^{-at}\,}$	${\displaystyle (s+a)^{-n}}$	${\displaystyle \operatorname {Re} (s)>-a}$
nth root	${\displaystyle {\sqrt[{n}]{t}}}$	${\displaystyle s^{-(n+1)/n}\cdot \Gamma \left(1+{\frac {1}{n}}\right)}$	${\displaystyle \operatorname {Re} (s)>0}$
Sine	${\displaystyle \sin(at)\,}$	${\displaystyle {\frac {a}{s^{2}+a^{2}}}}$	${\displaystyle \operatorname {Re} (s)>0}$
Cosine	${\displaystyle \cos(at)\,}$	${\displaystyle {\frac {s}{s^{2}+a^{2}}}}$	${\displaystyle \operatorname {Re} (s)>0}$
Hyperbolic sine	${\displaystyle \sinh(at)\,}$	${\displaystyle {\frac {a}{s^{2}-a^{2}}}}$	${\displaystyle \operatorname {Re} (s)>|a|\ }$
Hyperbolic cosine	${\displaystyle \cosh(at)\,}$	${\displaystyle {\frac {s}{s^{2}-a^{2}}}}$	${\displaystyle \operatorname {Re} (s)>|a|\ }$
Logarithm naturalis	${\displaystyle \ln(at)\,}$	${\displaystyle -{\frac {1}{s}}\left(\ln \left({\frac {s}{a}}\right)+\gamma \right)}$	${\displaystyle \operatorname {Re} (s)>0}$
Bessel function of the first kind of order 0	${\displaystyle J_{0}(at)\,}$	${\displaystyle {\frac {1}{\sqrt {s^{2}+a^{2}}}}\,}$	${\displaystyle \operatorname {Re} (s)>0}$
Modified Bessel function of the first kind of order 0	${\displaystyle I_{0}(at)\,}$	${\displaystyle {\frac {1}{\sqrt {s^{2}-a^{2}}}}\,}$	${\displaystyle \operatorname {Re} (s)>|a|}$
Bessel function of the first kind of order n	${\displaystyle J_{n}(at)\,}$	${\displaystyle {\frac {({\sqrt {s^{2}+a^{2}}}-s)^{n}}{a^{n}{\sqrt {s^{2}+a^{2}}}}}\,}$	${\displaystyle \operatorname {Re} (s)>0}$ ${\displaystyle (n>-1)\,}$
Modified Bessel function of the first kind of order n	${\displaystyle I_{n}(at)\,}$	${\displaystyle {\frac {(s-{\sqrt {s^{2}-a^{2}}})^{n}}{a^{n}{\sqrt {s^{2}-a^{2}}}}}\,}$	${\displaystyle \operatorname {Re} (s)>|a|}$ ${\displaystyle (n>-1)\,}$
Laguerre polynomials of order n	${\displaystyle L_{n}(at)\,}$	${\displaystyle {\frac {(s-a)^{n}}{s^{n+1}}}\,}$	${\displaystyle \operatorname {Re} (s)>0}$

example

The following shows the solution of the initial value problem of an ordinary first-order differential equation with constant coefficients using the Laplace transform:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}f(t)+\lambda f(t)=0}$

with . Using the linearity of the Laplace transformation and the behavior in the case of derivation in the original area (see table of general properties), the transform is given by ${\displaystyle f(0)=f_{0}}$

${\displaystyle (sF(s)-f_{0})+\lambda F(s)=0\ \rightarrow \ F(s)={\frac {f_{0}}{s+\lambda }}}$

with . The back transformation to the original area is listed in the above correspondence table (see exponential function), ${\displaystyle F(s)={\mathcal {L}}\{f(t)\}}$

${\displaystyle f(t)=f_{0}\ {\mathcal {L}}^{-1}\left\{{\frac {1}{s+\lambda }}\right\}=f_{0}e^{-\lambda t}}$

The above differential equation describes simple growth and decrease processes and is therefore found in many areas, including: a. in natural, economic and social sciences.

Laplace transform for dimensions

The Laplace transform is also used in probability theory and measure theory as a transformation of probability measures and measures . For a finite measure on the Laplace transform is defined here as ${\displaystyle \mu }$ ${\displaystyle [0,+\infty )}$

${\displaystyle {\mathcal {L}}_{\mu }(\lambda ):=\int \exp(-\lambda x)\mu (\mathrm {d} x)}$,

where is. For a random measure , the Laplace transform is defined as ${\displaystyle \lambda \geq 0}$ ${\displaystyle X}$

${\displaystyle {\mathcal {L}}_{X}(f)=\operatorname {E} \left(\exp \left(-\int f\,\mathrm {d} X\right)\right)}$

for positive, real-valued measurable functions . ${\displaystyle f}$

literature

• Lothar Berg : Operator calculation. Volume 2: Function Theoretical Methods. VEB Deutscher Verlag der Wissenschaften, Berlin 1974.
• William E. Boyce, Richard C. DiPrima: Ordinary Differential Equations. Introduction, tasks, solutions . Spectrum - Akademischer Verlag, Heidelberg et al. 1995, ISBN 3-86025-151-1 , 6 The Laplace Transformation, p. 349-400 .
• Hans Jörg Dirschmid: Mathematical basics of electrical engineering . 2nd, revised edition. Vieweg, Braunschweig et al. 1987, ISBN 3-528-13034-2 , pp. 774-806 .
• Gustav Doetsch: Introduction and application of the Laplace transformation (=  textbooks and monographs from the field of exact sciences. Mathematical series . Volume 24 ). 3. Edition. Birkhäuser, Basel et al. 1976, ISBN 3-7643-0784-6 .
• Otto Föllinger : Laplace, Fourier and z transformation . Modifications made by Mathias Kluwe. 8th, revised edition. Hüthig, Heidelberg 2003, ISBN 3-7785-2911-0 .
• Wolfgang Preuss: Functional Transformations. Fourier, Laplace and Z transforms . Fachbuchverlag Leipzig in Carl-Hanser-Verlag, Munich et al. 2002, ISBN 3-446-22015-1 .
• Murray R. Spiegel: Laplace Transformations. Theory and application . McGraw-Hill Book Company, 1977, ISBN 0-07-092013-3 .
• Georg Uszczapowski: The Laplace Transformation (=  German pocket books . Volume 22 ). Harri Deutsch, Zurich et al. 1974, ISBN 3-87144-169-4 .
• Hubert Weber: Laplace transformation for electrical engineers (=  Teubner study scripts . Volume 69 ). 2nd, revised edition. Teubner, Stuttgart 1978, ISBN 3-519-10069-X .

Web links

• Eric Weisstein: Laplace Transform . In: MathWorld (English).
• Laplace Transformation : Tasks and Interactive Tasks
• Video: Laplace transform of derivatives . Jörn Loviscach 2011, made available by the Technical Information Library (TIB), doi : 10.5446 / 10275 .

Individual evidence

1. ↑ József Miksa Petzval: Integration of the linear differential equations . 2 volumes (1853-1859). Vienna.
2. ↑ Gerhard Wunsch : Mathematical Methods in Electrical Engineering . II edition. tape 2 : lesson . Verlag technology, Berlin 1967. Eugen Philippow : Fundamentals of electrical engineering . 2nd Edition. Academic publishing company Geest & Portig K.-G., Leipzig 1967.
   
3. ^ Bronstein, et al .: Taschenbuch der Mathematik. 7th edition, Verlag Harri Deutsch, p. 775, chap. 15.2.1.1.
4. ↑ Ernst Schmutzer: Fundamentals of theoretical physics: with a plan of mathematics for physicists. Basics of theoretical physics. Volume 2, p. 125.
5. ^ Bronstein, et al .: Taschenbuch der Mathematik. 7th edition, Verlag Harri Deutsch, p. 1118, chap. 21.13.
6. ↑ Achim Klenke: Probability Theory . 3. Edition. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6 , p. 304 , doi : 10.1007 / 978-3-642-36018-3 .
7. ↑ Achim Klenke: Probability Theory . 3. Edition. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6 , p. 553 , doi : 10.1007 / 978-3-642-36018-3 .