Bessel differential equation

The Bessel differential equation is a linear ordinary differential equation of the second order. It was named after the German mathematician Friedrich Wilhelm Bessel . Their solutions are called Bessel functions or cylinder functions .

Bessel differential equation

The Bessel differential equation is an ordinary linear differential equation of the second order, which is given by

${\displaystyle x^{2}{\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} f}{\mathrm {d} x}}+\left(x^{2}-\nu ^{2}\right)f=0}$

is defined, where and are real or complex numbers . The solutions are called Bessel functions -th order. ${\displaystyle x}$ ${\displaystyle \nu }$ ${\displaystyle \nu }$

Correspondingly, the Bessel operator is a second order differential operator . It is defined by

${\displaystyle B_{\nu }:=x^{2}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} }{\mathrm {d} x}}+\left(x^{2}-\nu ^{2}\right)\,.}$

With it one can express Bessel's differential equation briefly by

${\displaystyle B_{\nu }f=0}$

Bessel functions

General

The Bessel functions of the first type and ${\displaystyle J_{0},J_{1}}$ ${\displaystyle J_{2}}$

The Bessel functions of the second genus and ${\displaystyle Y_{0},Y_{1}}$ ${\displaystyle Y_{2}}$

The solutions to Bessel's differential equation are called Bessel functions . They play an important role in physics, since the Bessel differential equation represents the radial part of the Laplace equation in the case of cylindrical symmetry . The Bessel functions are encountered, among other things, in the investigation of the natural vibrations of a circular membrane or an organ pipe, the propagation of water waves in round containers, the conduction of heat in rods, the analysis of the frequency spectrum of frequency- modulated signals, the field distribution in the cross-section of circular waveguides , the stationary ones States of box potentials, power distribution in nuclear reactors , the intensity of light diffraction at circular holes as well as filters in electrical engineering ( Bessel filters ). The Bessel functions are one of the special functions because of their diverse applications in mathematical physics .

As a differential equation of the second order of derivation, Bessel's differential equation has two linearly independent solutions . They can be described in different ways.

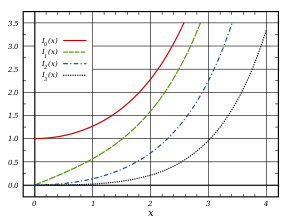
Bessel functions of the first kind ${\displaystyle J_{\nu }}$

The first- order Bessel functions are defined as ${\displaystyle J_{\nu }}$ ${\displaystyle \nu }$

${\displaystyle J_{\nu }(x)=\sum _{r=0}^{\infty }{\frac {(-1)^{r}\left({\frac {x}{2}}\right)^{2r+\nu }}{\Gamma (\nu +r+1)r!}}\,}$,

where is the gamma function . In the origin ( ) these functions are finite for integers . ${\displaystyle \Gamma (\cdot )}$ ${\displaystyle x=0}$ ${\displaystyle \nu }$

For non-integer are and linearly independent solutions. ${\displaystyle \nu }$ ${\displaystyle J_{\nu }}$ ${\displaystyle J_{-\nu }}$

The relationship applies to integers ${\displaystyle \nu }$

${\displaystyle J_{-\nu }(x)=(-1)^{\nu }J_{\nu }(x)=J_{\nu }(-x)\,}$.

In this case, the second independent solution is the Bessel function of the second kind, which is discussed below.

Integral representations

For whole numbers, the Bessel function of the first kind can also be represented as an integral: ${\displaystyle \nu }$

${\displaystyle {\begin{aligned}J_{\nu }(x)&={\frac {1}{\pi }}\int _{0}^{\pi }\cos(x\sin \varphi -\nu \varphi )\,\mathrm {d} \varphi \\&={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{\mathrm {i} \,(x\sin \varphi -\nu \varphi )}\,\mathrm {d} \varphi \,.\end{aligned}}}$

This is the -th Fourier coefficient of the function . ${\displaystyle J_{\nu }(x)}$ ${\displaystyle \nu }$ ${\displaystyle \varphi \mapsto e^{ix\sin \varphi }}$

Hypergeometric function

The Bessel function of the first kind can be expressed by the generalized hypergeometric function :

${\displaystyle J_{\nu }(x)={\frac {(x/2)^{\nu }}{\Gamma (\nu +1)}}\;_{0}F_{1}(;\nu +1;-x^{2}/4).}$

This expression is related to the development of the Bessel function in relation to the Bessel-Clifford function .

Bessel functions of the second kind ${\displaystyle Y_{\nu }}$

The Bessel functions of the second kind (also called Weber functions or Neumann functions) also solve Bessel's differential equation. An alternative name is . For non-integers , they can be defined by ${\displaystyle Y_{\nu }(x)}$ ${\displaystyle N_{\nu }(x)}$ ${\displaystyle \nu }$ ${\displaystyle Y_{\nu }(x)}$

${\displaystyle Y_{\nu }(x)={\frac {J_{\nu }(x)\cos(\nu \pi )-J_{-\nu }(x)}{\sin(\nu \pi )}}.}$

For integers is the function formed by the limit crossing ${\displaystyle n}$ ${\displaystyle \nu \rightarrow n}$

${\displaystyle Y_{n}(x)=\lim _{\nu \to n}Y_{\nu }(x)}$

also a solution of Bessel's differential equation.

As for the Bessel functions of the first type, the following relationship also applies to the Bessel functions of the second type:

${\displaystyle Y_{-n}(x)=(-1)^{n}Y_{n}(x)}$.

After crossing the border with the rule of de l'Hospital, this results

${\displaystyle Y_{n}(x)={\frac {1}{\pi }}\left[{\operatorname {d} \over \operatorname {d} \!\nu }J_{\nu }(x){\Big |}_{\nu =n}+(-1)^{n}{\operatorname {d} \over \operatorname {d} \!\nu }J_{\nu }(x){\Big |}_{\nu =-n}\right].}$

One finds explicit

${\displaystyle Y_{n}(x)=\,{\frac {2}{\pi }}\left(\gamma +\ln {\frac {x}{2}}\right)J_{n}(x)-{\frac {1}{\pi }}\sum _{k=0}^{n-1}{\frac {(n-k-1)!}{k!}}\left({\frac {x}{2}}\right)^{2k-n}-{\frac {1}{\pi }}\sum _{k=0}^{\infty }(-1)^{k}{\frac {H_{k}+H_{k+n}}{k!(n+k)!}}\left({\frac {x}{2}}\right)^{2k+n}}$

for . Here is the Euler-Mascheroni constant and the -th harmonic number . ${\displaystyle n\in \mathbb {N} _{0}}$ ${\displaystyle \gamma }$ ${\displaystyle H_{n}}$ ${\displaystyle n}$

The Bessel functions of the second kind have a logarithmic singularity and a pole -th order. ${\displaystyle x=0}$ ${\displaystyle n}$

For all of them , in addition to the Bessel function of the first type, the Bessel function of the second type is a second, linearly independent solution. ${\displaystyle \nu }$ ${\displaystyle J_{\nu }}$ ${\displaystyle Y_{\nu }}$

Bessel functions of the third kind ${\displaystyle H_{\nu }^{(1)},H_{\nu }^{(2)}}$

The Bessel functions of the third kind , (also known as Hankel are functions) linear combinations of Bessel functions of the first and second generic ${\displaystyle H_{\nu }^{(1)}}$ ${\displaystyle H_{\nu }^{(2)}}$

${\displaystyle {\begin{aligned}H_{\nu }^{(1)}(x)&=J_{\nu }(x)+\mathrm {i} \cdot Y_{\nu }(x)\,,\\H_{\nu }^{(2)}(x)&=J_{\nu }(x)-\mathrm {i} \cdot Y_{\nu }(x)\,,\end{aligned}}}$

where denotes the imaginary unit . These two functions are also linearly independent solutions of the Bessel differential equation. ${\displaystyle \mathrm {i} }$

properties

Relationships of orders of a genus

• For the Bessel functions , , and apply Rekursionsbeziehungen : ${\displaystyle J_{\nu }}$ ${\displaystyle Y_{\nu }}$ ${\displaystyle H_{\nu }^{(1)}}$ ${\displaystyle H_{\nu }^{(2)}}$

${\displaystyle {\frac {\nu }{x}}\Omega _{\nu }={\frac {1}{2}}(\Omega _{\nu -1}+\Omega _{\nu +1})}$,

${\displaystyle {\frac {\rm {d}}{{\rm {d}}x}}\Omega _{\nu }={\frac {1}{2}}(\Omega _{\nu -1}-\Omega _{\nu +1})}$.

• For true . ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle \sum _{n=-\infty }^{\infty }J_{n}(x)^{2}=1}$

• For true . ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle \left(-{\frac {1}{x}}{\frac {\rm {d}}{{\rm {d}}x}}\right)^{n}J_{0}(x)={\frac {J_{n}(x)}{x^{n}}}}$

Asymptotic behavior

Let then hold for the asymptotic representations ${\displaystyle x,\nu \in \mathbb {R} ,\nu \geq 0}$ ${\displaystyle 0<x\ll {\sqrt {\nu +1}}}$

${\displaystyle {\begin{aligned}J_{\nu }(x)&\approx {\frac {1}{\Gamma (\nu +1)}}\left({\frac {x}{2}}\right)^{\nu }\\Y_{\nu }(x)&\approx {\begin{cases}{\frac {2}{\pi }}\left(\ln \left({\frac {x}{2}}\right)+\gamma \right)&{\text{wenn }}\nu =0\\\\-{\frac {\Gamma (\nu )}{\pi }}\left({\frac {2}{x}}\right)^{\nu }&{\text{wenn }}\nu >0.\end{cases}}\end{aligned}}}$

For big arguments one finds ${\displaystyle x\gg |\nu ^{2}-1/4|}$

${\displaystyle {\begin{aligned}J_{\nu }(x)&\approx {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\nu \pi }{2}}-{\frac {\pi }{4}}\right)\\Y_{\nu }(x)&\approx {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\nu \pi }{2}}-{\frac {\pi }{4}}\right).\end{aligned}}}$

These formulas are for exact. Compare with the spherical Bessel functions below. ${\displaystyle \nu =1/2}$

Modified Bessel functions

The modified Bessel functions of the first kind for and ${\displaystyle I_{0},I_{1},I_{2}}$ ${\displaystyle I_{3}}$

The modified Bessel functions of the second kind for and ${\displaystyle K_{0},K_{1},K_{2}}$ ${\displaystyle K_{3}}$

The differential equation

${\displaystyle x^{2}{\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} f}{\mathrm {d} x}}-(x^{2}+\nu ^{2})f=0}$

is solved by Bessel functions with a purely imaginary argument. The modified Bessel functions are normally defined for their solution

${\displaystyle {\begin{aligned}I_{\nu }(x)&=i^{-\nu }J_{\nu }(ix)=\sum _{r=0}^{\infty }{\frac {({\frac {x}{2}})^{2r+\nu }}{\Gamma (r+\nu +1)r!}}\\K_{\nu }(x)&={\frac {\pi }{2}}{\frac {I_{-\nu }(x)-I_{\nu }(x)}{\sin(\nu \pi )}}={\frac {\pi }{2}}i^{\nu +1}H_{\nu }^{(1)}(ix)\\&={\frac {\pi }{2}}(-i)^{\nu +1}H_{\nu }^{(2)}(-ix)\end{aligned}}}$

The function is also known as the MacDonald function . In contrast to the "normal" Bessel functions, the modified Bessel functions do not have an oscillating, but an exponential behavior. ${\displaystyle K_{\nu }(x)}$

Airy integrals

An integral representation can be given for the functions and ${\displaystyle K_{1/3}}$ ${\displaystyle K_{2/3}}$

${\displaystyle {\begin{aligned}K_{1/3}(x)&={\sqrt {3}}\int _{0}^{\infty }\cos \left({\frac {3}{2}}x\left(u+{\frac {u^{3}}{3}}\right)\right)\mathrm {d} u\\K_{2/3}(x)&={\sqrt {3}}\int _{0}^{\infty }u\sin \left({\frac {3}{2}}x\left(u+{\frac {u^{3}}{3}}\right)\right)\mathrm {d} u\end{aligned}}}$.

Hypergeometric function

The modified Bessel function of the first kind can also be expressed by a generalized hypergeometric function :

${\displaystyle I_{\nu }(x)={\frac {(x/2)^{\nu }}{\Gamma (\nu +1)}}\;_{0}F_{1}(\nu +1;x^{2}/4)}$.

Relationships of orders of a genus

• The recursion relationships apply to the Bessel functions and : ${\displaystyle K_{\nu }}$ ${\displaystyle I_{\nu }}$

${\displaystyle {\frac {\nu }{x}}K_{\nu }=-{\frac {1}{2}}\left(K_{\nu -1}-K_{\nu +1}\right)}$

${\displaystyle {\frac {\nu }{x}}I_{\nu }={\frac {1}{2}}\left(I_{\nu -1}-I_{\nu +1}\right)}$

${\displaystyle {\frac {\rm {d}}{{\rm {d}}x}}K_{\nu }=-{\frac {1}{2}}(K_{\nu -1}+K_{\nu +1})}$

${\displaystyle {\frac {\rm {d}}{{\rm {d}}x}}I_{\nu }={\frac {1}{2}}(I_{\nu -1}+I_{\nu +1})}$

Asymptotic behavior

We again assume that is real and non-negative. For small arguments one finds ${\displaystyle \nu }$ ${\displaystyle 0<x\ll {\sqrt {\nu +1}}}$

${\displaystyle {\begin{aligned}I_{\nu }(x)&\approx {\frac {1}{\Gamma (\nu +1)}}\left({\frac {x}{2}}\right)^{\nu }\\\\K_{\nu }(x)&\approx {\begin{cases}-\left(\ln \left({\frac {x}{2}}\right)+\gamma \right)&{\text{wenn }}\nu =0\\\\{\frac {\Gamma (\nu )}{2}}\left({\frac {2}{x}}\right)^{\nu }&{\text{wenn }}\nu >0\,.\end{cases}}\end{aligned}}}$

For big arguments you get ${\displaystyle x\gg |\nu ^{2}-1/4|}$

${\displaystyle {\begin{aligned}I_{\nu }(x)&\approx {\frac {1}{\sqrt {2\pi x}}}e^{x}\left(1+{\mathcal {O}}\left({\frac {1}{x}}\right)\right)\\\\K_{\nu }(x)&\approx {\sqrt {\frac {\pi }{2x}}}e^{-x}\left(1+{\mathcal {O}}\left({\frac {1}{x}}\right)\right)\,.\end{aligned}}}$

Spherical armchair functions

The Helmholtz equation in spherical coordinates leads to the radial equation after separating the variables

${\displaystyle x^{2}{\frac {\mathrm {d} ^{2}f_{\mu }(x)}{\mathrm {d} x^{2}}}+2x{\frac {\mathrm {d} f_{\mu }(x)}{\mathrm {d} x}}+[x^{2}-\mu (\mu +1)]f_{\mu }(x)=0}$.

After the substitution

${\displaystyle f_{\mu }(x)={\frac {1}{\sqrt {x}}}u_{\mu }(x)}$

one obtains the Bessel differential equation ${\displaystyle (\nu =\mu +1/2)}$

${\displaystyle x^{2}{\frac {\mathrm {d} ^{2}u_{\mu }(x)}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} u_{\mu }(x)}{\mathrm {d} x}}+\left[x^{2}-\left(\mu +{\frac {1}{2}}\right)^{2}\right]u_{\mu }(x)=0}$.

For the solution of the radial equation, the spherical Bessel functions , the spherical Neumann functions and the spherical Hankel functions are usually defined: ${\displaystyle f_{\mu }(x)}$ ${\displaystyle j_{\mu }(x)}$ ${\displaystyle y_{\mu }(x)=n_{\mu }(x)}$ ${\displaystyle h_{\mu }^{(1,2)}(x)}$

${\displaystyle {\begin{aligned}&j_{\mu }(x)\quad ={\sqrt {\frac {\pi }{2x}}}J_{\mu +1/2}(x)\\&y_{\mu }(x)\quad ={\sqrt {\frac {\pi }{2x}}}Y_{\mu +1/2}(x)\\&h_{\mu }^{(1,2)}(x)={\sqrt {\frac {\pi }{2x}}}H_{\mu +1/2}^{(1,2)}=j_{\mu }(x)\pm iy_{\mu }(x)\end{aligned}}}$.

The alternative representations for ${\displaystyle m\in \mathbb {N} }$

${\displaystyle {\begin{aligned}&j_{m}(x)\quad =(-x)^{m}\left({\frac {1}{x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{m}\ {\frac {\sin x}{x}}\\&y_{m}(x)\quad =-(-x)^{m}\left({\frac {1}{x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{m}\ {\frac {\cos x}{x}}\\&h_{m}^{(1,2)}(x)=\mp i(-x)^{m}\left({\frac {1}{x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{m}{\frac {e^{\pm ix}}{x}}\\\end{aligned}}}$

The spherical Bessel and Hankel functions are required, for example, for the treatment of the spherically symmetrical potential well in quantum mechanics .

properties

• For the spherical Bessel functions , , and apply Rekursionsbeziehungen : ${\displaystyle j_{\mu }}$ ${\displaystyle y_{\mu }}$ ${\displaystyle h_{\mu }^{(1)}}$ ${\displaystyle h_{\mu }^{(2)}}$

${\displaystyle {\begin{aligned}&{\frac {2\mu +1}{x}}\omega _{\mu }(x)\;\,=\omega _{\mu -1}(x)+\omega _{\mu +1}(x)\\&(2\mu +1)\omega '_{\mu }(x)\,=\mu \omega _{\mu -1}(x)-(\mu +1)\omega _{\mu +1}(x)\\&{\frac {\mathrm {d} }{\mathrm {d} x}}(x\omega _{\mu }(x))\quad =x\omega _{\mu -1}(x)-\mu \omega _{\mu }(x)\end{aligned}}}$.

• For the Wronsky determinant we have

${\displaystyle W(j_{\mu },y_{\mu })={\frac {1}{i}}W(j_{\mu },h_{\mu }^{(1)})=-W(y_{\mu },h_{\mu }^{(1)})={\frac {1}{x^{2}}}}$.

Hankel transformation

→ Main article : Hankel transformation

The Hankel transform is an integral transform that is closely related to the Fourier transform . The integral kernel of the Hankel transformation is the Bessel function of the first kind , that is, the integral operator is: ${\displaystyle J_{n}}$

${\displaystyle H_{n}[f](s)=\int _{0}^{\infty }J_{n}(ts)tf(t)\mathrm {d} t}$.

A special property of the Hankel transformation is that it can be used to convert the Bessel operator into an algebraic expression (a multiplication).

history

Bessel functions were dealt with in detail by Bessel in 1824, but also appeared before that in the case of special physical problems, for example in Daniel Bernoulli (vibration of heavy chains 1738), Leonhard Euler (membrane vibration 1764), in celestial mechanics by Joseph-Louis Lagrange (1770 ) and with Pierre-Simon Laplace , in heat conduction with Joseph Fourier (heat propagation in the cylinder 1822) and Siméon Denis Poisson (1823).

literature

• Milton Abramowitz , Irene Stegun : Handbook of Mathematical Functions. Dover, New York 1972, p. 355 .
• JH Graf, E. Gubler: Introduction to the theory of Bessel functions. First volume Second volume . KJ Wyss, Bern 1900
• Carl Gottfried Neumann : Theory of Bessel's functions, an analogue to the theory of spherical functions. BG Teubner, Leipzig 1867.
• Paul Schafheitlin The theory of Bessel functions . BG Teubner, Leipzig 1908.
• GN Watson A Treatise on the Theory of Bessel functions , Cambridge University Press 1922, 1944, Archives

Bessel functions are dealt with in many textbooks in theoretical physics. B .:

• John David Jackson : Classical Electrodynamics. John Wiley, New York NY 1962 (3rd edition. Ibid 1999, ISBN 0-471-30932-X ; German: 4th revised edition. De Gruyter, Berlin et al. 2006, ISBN 3-11-018970-4 ).
• Wolfgang Nolting: Basic course Theoretical Physics 5/2. Quantum Mechanics - Methods and Applications , 6th edition, Springer textbook, 2006, ISBN 978-3-540-26035-6
• Arnold Sommerfeld Lectures on Theoretical Physics , Volume 6: Partial Differential Equations of Physics , Harri Deutsch 1992, ISBN 3-87144-379-4 .

Individual evidence

1. ^ Bessel operator . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 978-3-8274-0439-8 .
2. ^ Friedrich Wilhelm Bessel: Investigation of the part of the planetary disturbances, which arises from the movement of the sun. In: Treatises of the Berlin Academy of Sciences 1824, Math. Classe, pp. 1–52, Berlin 1826.
3. ^ Jacques Dutka: On the early history of Bessel functions. In: Archive for History of Exact Sciences . Volume 49, 1995, pp. 105-134.
4. ^ GN Watson: Theory of Bessel Functions. Cambridge University Press, 1944, Chapter 1 (for history).

Web links

• Eric W. Weisstein : Bessel Differential Equation . In: MathWorld (English).
• ( Page no longer retrievable , search in web archives: Bessel functions ν-th order with real argument - JavaScript )