Frequency modulation
The frequency modulation ( FM ) is a modulation method in which the carrier frequency is changed by the signal to be transmitted. The frequency modulation enables a higher dynamic range of the information signal compared to the amplitude modulation . It is also less prone to interference. The method was mathematically investigated by John Renshaw Carson as early as 1922 and first implemented in practice by Edwin Howard Armstrong . Frequency modulation is an angle modulation and is related to phase modulation . The phase angle is influenced for both .
It is not to be confused with the channel coding known as digital frequency modulation or also as Miller code , which is used, for example, in magnetic data carriers for data recording.
General
modulation
A frequency-modulated signal can be generated at high frequencies with the aid of an oscillator circuit whose frequency-determining resonant circuit contains a voltage-dependent capacitance, typically a capacitance diode , to which the modulation signal is applied as a signal voltage. This changes the capacitance of the diode and thus also the resonance frequency of the resonant circuit. FM at low frequencies is easier to generate with voltage controlled oscillators . A direct digital synthesis circuit (DDS) or quadrature amplitude modulation (IQ modulation) can advantageously be used for digital generation of a frequency-modulated signal .
Demodulation
Before demodulation, the amplitude of the FM signal is kept constant (“limited”) in order to eliminate any changes in amplitude that may arise from interference on the transmission path. This is possible because the amplitude does not contain any information. Usually a chain of differential amplifiers is used for this .
The received FM signal is seldom immediately demodulated, but first transferred to an intermediate frequency according to the superhet principle ; this process is known as mixing . For example, FM radio is transmitted on the carrier frequency f = 100 MHz with a frequency deviation Δ f T = ± 75 kHz. The relative stroke is
and does not allow problem-free demodulation. By converting it to the intermediate frequency of 10.7 MHz customary for VHF receivers, H is increased approximately tenfold and the circuit is simplified. Narrowband FM such as slow scan television cannot be demodulated at all without this previous frequency change.
There are several types of FM demodulators. A discriminator first converts the FM signal into amplitude or pulse modulation. In the early days, simple edge rectifiers were used for this , later ratio detectors . In the coincidence demodulator , a phase-modulated signal is formed from the frequency-modulated signal, which can then be demodulated. Another possibility is the PLL demodulator. By phase comparison of the modulated signal with the signal of a local oscillator, a voltage is obtained corresponding to the deviation with which the PLL oscillator is readjusted. The control voltage is also the LF output signal. PLL demodulation provides high reception quality and security, but it was expensive until the use of specially developed integrated circuits became popular.
A control voltage is often obtained from the output voltage of the FM demodulator, which is used to track the receiver's oscillator ( Automatic Frequency Control , AFC for short) in order to keep the signal in the middle of the pass band of the IF filter and thus the distortion low .
Frequency modulation parameters
One calls caused by the modulation change in the carrier frequency with .DELTA.f T (also frequency deviation or short stroke called), the change in phase angle of the carrier with and the ratio of the frequency deviation to the modulation frequency as the modulation index η:
where represents the highest useful signal frequency to be transmitted (bandwidth of the useful signal).
The Carson formula applies approximately to the bandwidth of the frequency-modulated signal :
(with a modulation index η greater than 1).
All spectral lines are recorded up to 10% of the carrier's amplitude. This means that 90% of the spectral lines lie within the calculated bandwidth (bandwidth of medium transmission quality). If one takes into account spectral lines up to 1% of the carrier amplitude, the bandwidth for a high transmission quality, with 99% of the spectral lines in the bandwidth, results (also referred to as Carson's formula) by:
(with a modulation index η greater than 1).
The frequency-modulated VHF radio is given as a specific example of the parameters shown: Mono programs work with a frequency deviation Δ f T = 75 kHz and a limit frequency of the audio signal of f S = 15 kHz. This results in a modulation index η = 5 for VHF radio and a required bandwidth B 10% = 180 kHz in the VHF band. For VHF stereo radio including the data signal from the Radio Data System (RDS), the baseband bandwidth is f S = 60 kHz and the required VHF bandwidth is just under 400 kHz. Neighboring FM stereo transmitters must transmit at least 400 kHz offset so as not to interfere with each other.
Under narrowband FM frequency modulation is understood, the modulation index η is less than 2, it is referred to as wideband FM designated. Analogue VHF radio is one of the broadband FM , narrowband FM is used, among other things, in the area of amateur radio such as in the 70 cm band .
Illustration of frequency modulation
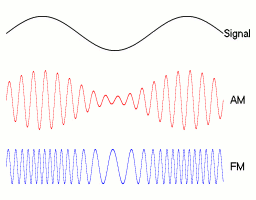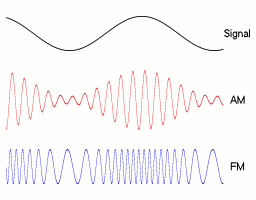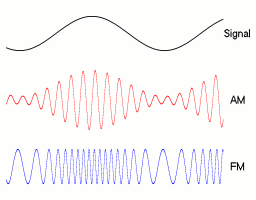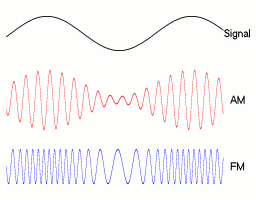
The upper diagram of Figure 1 shows a frequency-modulated signal and the information signal in dashed lines. In the example, the carrier has 15 times the frequency of the signal, the signal is a simple cosine. It can be seen that where the instantaneous value of the voltage of the signal is lowest, the frequency of the modulated signal is also lowest. During the zero point crossing of the information signal, the modulated carrier has the same frequency as the unmodulated carrier. The frequency of the information signal depends on how often the carrier frequency changes per second. The amplitude of the signal depends on how large the frequency change (stroke) is. The more often per second the frequency of the carrier changes, the greater the frequency of the information signal. The greater the stroke, the greater the amplitude of the information signal. The greater the amplitude or frequency of the information signal, the greater the bandwidth required.
In the middle diagram of Figure 1, the change in the frequency of the carrier as a function of the above signal is shown, with the unmodulated carrier dashed. The lower diagram of Figure 1 shows the phase angle of the carrier in rad. The unmodulated carrier is shown in dashed lines. The phase indicator of the carrier rotates continuously, which is why the graph rises even with an unmodulated signal. The solid line represents the phase angle of the modulated signal. However , it is not proportional to the instantaneous value of the signal voltage. and are shifted by 90 °.
Frequency spectrum with frequency modulation
With a frequency-modulated signal, side oscillations occur at a distance of the signal frequency from the carrier frequency. Theoretically, there are an infinite number of side vibrations. In practice, side vibrations less than 10% of the amplitude of the unmodulated carrier are neglected, which results in the Carson formula for the bandwidth. The level of the individual side vibrations and thus the power distribution as a function of is determined using a Bessel function diagram with the modulation indices.
The equation for the individual components of frequency modulation is:
The factors must be read from the Bessel diagram for a given . In certain cases , the carrier or side oscillation pairs can disappear. Based on this, it can also be seen that the performance ratio between the carrier and side vibrations becomes unfavorable.
Since frequency modulation becomes smaller as the signal frequency increases , high frequencies can be transmitted more poorly with frequency modulation, in contrast to phase modulation, since the lateral vibration components become smaller and smaller. Often you turn on FM so before modulation, a pre-emphasis to the signal at what a to the high frequencies to increase, de-emphasis is reversed in the receiver.
Relationship between frequency modulation and phase modulation
Frequency modulation and phase modulation are mathematically closely related. A phase modulation of a sinusoidal carrier can be expressed very easily. First the unmodulated carrier:
The term denotes the current phase. is the carrier angular frequency , is a constant, the phase at the point in time . We can write the current phase as a function of time .
Now the current phase is changed by adding a modulator, which gives the expression for a phase modulation:
Here referred to the amount of modulation and the modulating function or just the modulator. Corresponding:
- .
You can see that phase modulation is very easy to express mathematically.
A frequency modulation assumes that the frequency changes constantly. This can no longer be a term of the form to express, but we need to introduce the concept of instantaneous angular frequency: . The instantaneous frequency is therefore quite generally the time derivative of the phase function (cf. in this context the relationship between speed and location and the analogy between phase and location or frequency and speed). This is the core of the relationship between frequency and phase modulation. From this point of view, let's look again at the phase of the unmodulated carrier:
The time derivative is:
- .
The newly introduced term of the instantaneous frequency therefore also sensibly includes the case of constant frequency. Frequency modulation is now demanding that the instantaneous frequency according to the following protocol behaves: . For the calculation of the curve shape at any point in time, however, we do not need the current frequency, but the phase function. If the frequency is the derivative of the phase, then conversely the phase is the integral of the frequency:
for example:
This gives the following expression for the frequency modulation:
The direct comparison with the expression for the phase modulation shows:
The interpretation of this fact becomes clear in the following example. Set , then we get for the modulations:
and
- .
The phase deviation is still there for the phase modulation , one obtains for the frequency modulation . The current frequency is for phase modulation and for frequency modulation . In both cases there is a modulation of the phase. However, with frequency modulation, the modulator does not have a direct effect on the phase, but the integral of the modulator must first be calculated. The integral has a low-pass effect. The phase deviation therefore decreases with frequency modulation as the frequency of the modulator increases. Conversely, the frequency deviation in phase modulation becomes smaller and smaller as the modulator frequency decreases.
In typical analog oscillators with RC or LC elements, differential equations occur in which z. B. currents are integrated. As a result, frequency modulation always occurs with the simplest means. A change in the manipulated variable changes the frequency in a controlled manner and only indirectly changes the phase. Phase modulation, on the other hand, is very difficult in analogue fashion, since direct access to the phase function is usually not possible. With digital oscillators, both are possible in a simple manner, because there is direct access to the phase indicator.
Modulation gain, noise-limited sensitivity
Compared to amplitude demodulation (AM), an FM demodulator has a modulation gain - it evaluates the noise less than the useful signal. If there is insufficient carrier-to-noise ratio (CNR of English. Carrier to Noise Ratio ) loses this FM modulation gain. Errors in the determination of the instantaneous frequency occur due to phase jumps, which are expressed as short needle pulses in the signal. This loss of modulation gain begins below 12 dB CNR and leads to a severe deterioration in reception below 5.5… 9 dB CNR ( FM threshold ).
The "fish formation" in analog satellite reception is z. B. due to this problem.
Application of frequency modulation
Radio technology
FM enables high quality, low-interference wireless transmission of radio programs . It is also used for television sound and often also for voice radio . While with AM the signal cannot be completely separated from the noise even with a narrowband filter, with the FM receiver it is possible to improve the quality significantly despite the broadband filter:
- the demodulator ( ratio detector , coincidence demodulator , PLL demodulator) is hardly influenced by amplitude fluctuations
- Amplitude fluctuations are also reduced by a signal limitation ( limiter amplifier )
- the transmission power is constantly high
- Frequency response errors during demodulation result in only minor non-linear distortions
- Co-channel interference - that is, in the same frequency range - generates less AF interference than when using AM
- Shrinkage phenomena have hardly any influence - the reception field strength may fluctuate
The first application of FM to VHF radio resulted in the technically incorrect equation of the terms FM and VHF , especially in the English-speaking area .
Audio / video technology
The video signal and the sound in video recorders are recorded with frequency modulation. Analog satellite TV is also frequency modulated.
measuring technology
By periodically changing the frequency of a measurement generator ( wobble generator ) within a certain range, the transmission characteristic of an electrical assembly (e.g. bandpass ) or an entire system can be determined. The amplitude response is plotted as a function of the frequency. This process is also known as wobbling .
Television technology
The audio channel is always transmitted frequency-modulated on its own carrier on analog television channels. The carrier frequency is 5.5 MHz ( CCIR ) or 6.5 MHz ( OIRT ) next to the video carrier frequency . In the receiver, the difference frequency is obtained by mixing image and sound carrier frequencies and, after filtering, demodulated as in FM reception. The SECAM television standard uses FM to transmit color information.
FM system for the hard of hearing
For sound transmission of radio and television sound as well as in school classes and conference rooms, special FM sound transmission systems for the hard of hearing are used.
Digital technology
Using frequency shift keying and similar methods, binary information can be encoded and transmitted over longer distances (for example over telephone lines).
Printing technology
Frequency- modulated screening : screening process that works with very small pixels of the same size. The image reproduction is achieved by scattering the points with different densities. Light image areas have fewer image points , deep image areas have more. In contrast to this, the classic amplitude-modulated screen controls the image reproduction by varying the point sizes and screen angles. FM screens enable photorealistic halftone reproduction and more detailed reproduction, even on low-resolution printers. Moiré effects are avoided. The resolution of the templates can also be lower than with amplitude-modulated rasters with a comparable print quality. A “restless” image can arise in smooth surfaces, homogeneous grid surfaces or gradients.
Electronic music
Main article: FM synthesis
Frequency modulation (FM) made it possible to generate quite complex sounds with the earliest analog modular synthesizers (around 1960). When switching to digital technology, they realized that it was much cheaper to use phase modulation (PM). This leads to a considerable tonal difference: one reason for this has already been mentioned above - it is the phase deviation that decreases with increasing modulator frequency with FM, which remains constant with PM. With PM, the strength of the partial tones remains constant even when the modulator frequency changes, which simplifies handling. The frequency deviations, which are difficult to control with FM, do not occur with PM because there is no direct access to the frequency. This makes programming sounds by means of PM compared to FM much easier for the musician. However, a vibrato created by PM becomes weaker as the frequency decreases.
The term FM continued to be used for historical reasons, e.g. B. in the devices of the company Yamaha (DX7 etc.).
Frequency modulations in acoustics
Frequency modulation often determines the character of sound bodies and musical instruments. On the other hand, it is undesirable for loudspeakers .
Sound body
Sound bodies that have an extensive surface (e.g. bells , gongs , tubes, plates, sheets) often carry out frequency-modulated natural oscillations :
A sheet of metal has a certain stiffness that allows it to resist attempts to bend it. This stiffness can be increased in one direction by means of a wave shape (corrugated iron).
If a flexural wave spreads over a flat sheet, such wave structures arise and disappear periodically. A higher-frequency wave of a (further) natural oscillation running perpendicular to this finds a stiffer or softer medium precisely in this rhythm; the frequency of this natural oscillation is therefore modulated in the rhythm of the flexural wave due to the resulting different propagation speed.
An example on which this can be demonstrated both statically and dynamically is a band made of spring steel that is variably bent by hand (e.g. a large saw blade), which is then struck.
Musical instruments
The strings of stringed instruments are frequency modulated by changing their length or tension. The former is used for vibrato and glissando on string instruments and also the sitar , the latter also for the sitar, but especially for guitars. The string tension is changed by pulling them to the side on the fingerboard or by moving the tailpiece on electric guitars (see Tremolo (guitar) ).
In addition, strings have an amplitude-dependent natural frequency, which is particularly important in the case of intestinal violins and stringed instruments with low string tension or high vibration amplitude.
With flutes, among other things, the sound frequency depends on the blowing pressure; in this way a frequency modulation can also be generated, which however also has an amplitude modulation ( tremolo ).
speaker
Frequency modulation occurs in loudspeakers that reproduce both high frequencies and low frequencies with a high amplitude; A frequency modulation of the high frequencies is created by the membrane moving towards and away from the listener in the rhythm of the low frequency ( Doppler effect ). The effect is undesirable and can be avoided by using two-way or multi-way boxes or a loudspeaker with a large membrane diameter.
Abbreviation of FM types
- F1 - frequency modulation; a single channel containing quantized or digital information (without the use of a modulating subcarrier)
- F2 - frequency modulation; a single channel containing quantized or digital information (using a modulating subcarrier)
- F3 - frequency modulation; a single channel containing analog information
literature
- Jürgen Detlefsen, Uwe Siart: Basics of high frequency technology. 2nd edition, Oldenbourg Verlag, Munich Vienna, 2006, ISBN 3-486-57866-9
- Gregor Häberle, Heinz Häberle, Thomas Kleiber: Expertise in radio, television and radio electronics. 3rd edition, Verlag Europa-Lehrmittel, Haan-Gruiten, 1996, ISBN 3-8085-3263-7
- Curt Rint : Handbook for high frequency and electrical technicians Volume 2. 13th edition, Hüthig and Pflaum Verlag GmbH, Heidelberg, 1981, ISBN 3-7785-0699-4
Web links
- Modulation method for voice transmission - PDF (186 kB)
- Modulation method - PDF (328 kB)
- Frequency modulation - PDF (827 kB)
- Modulation and Noise - PDF (642 kB)
- FM demodulation - PDF (708 kB)
- Digital and analog modulation methods - PDF (282 kB)
Individual evidence
-
^ John R. Carson: Notes on the Theory of Modulation . In: Proceedings of the IRE . tape 10 , no. 1 , 1922, pp. 57-64 . Reprint: John R. Carson: Notes on the theory of modulation . In: Proceedings of the IEEE . tape
51 , no. 6 , 1963, pp. 893-896 . - ↑ Stefan Steger, DL7MAJ: The types of modulation - theory and practical applications, lecture on the VHF-UHF 2002 in Munich. Retrieved March 1, 2015 .
- ↑ Alexander Braun, Markus Hofbauer: Term paper on digital satellite television . Zurich 1997 ( HTML - semester paper at the IKT of the ETH Zurich).
- ↑ Doppler effect in loudspeakers. Retrieved September 25, 2018 .













![{\ begin {matrix} u _ {\ mathrm {WM}} (t) = & {\ hat {U}} _ {\ mathrm {T}} \ cdot [\\ && J_ {0} (\ Delta \ varphi) \ cdot \ cos (\ omega _ {\ mathrm {T}} \ cdot t) & {\ text {(carrier portion)}} \\ && - J_ {1} (\ Delta \ varphi) \ cdot \ sin ((\ omega _ {\ mathrm {T}} - \ omega _ {\ mathrm {S}}) \ cdot t) & {\ text {(portion of first undershoot)}} \\ && - J_ {1} (\ Delta \ varphi) \ cdot \ sin ((\ omega _ {\ mathrm {T}} + \ omega _ {\ mathrm {S}}) \ cdot t) & {\ text {(portion of the first harmonic)}} \\ && - J_ { 2} (\ Delta \ varphi) \ cdot \ cos ((\ omega _ {\ mathrm {T}} -2 \, \ omega _ {\ mathrm {S}}) \ cdot t) & {\ text {(portion second undershoot)}} \\ && - J_ {2} (\ Delta \ varphi) \ cdot \ cos ((\ omega _ {\ mathrm {T}} +2 \, \ omega _ {\ mathrm {S}}) \ cdot t) & {\ text {(second harmonic component)}} \\ && + J_ {3} (\ Delta \ varphi) \ cdot \ sin ((\ omega _ {\ mathrm {T}} -3 \, \ omega _ {\ mathrm {S}}) \ cdot t) & {\ text {(third undershoot component)}} \\ && + J_ {3} (\ Delta \ varphi) \ cdot \ sin ((\ omega _ {\ mathrm {T}} +3 \, \ omega _ {\ mathrm {S}}) \ cdot t) & {\ text {(third harmonic component)}} \\ & \ ldots] & \ end {matrix} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/85eac004bddc5e4c738eb573ed3478496d887a50)




























