Amplitude modulation

With amplitude modulation ( AM ), the amplitude of a high-frequency oscillation fluctuates at a low frequency. AM is still used as a type of modulation in broadcasting . Amplitude modulation also occurs naturally; in music as a tremolo .

Low-frequency useful signals such as speech or music often cannot be transmitted directly via the desired transmission media such as a radio channel . For transmission, the useful signal must be shifted to a different frequency range , which can be achieved, for example, by AM. By shifting, several useful signals can be transmitted simultaneously and without mutual interference.

Comparison of amplitude and frequency modulation

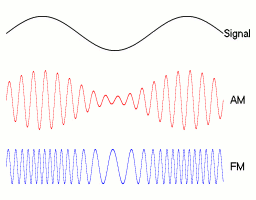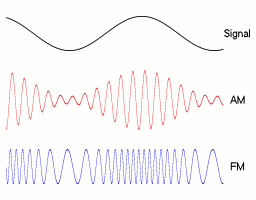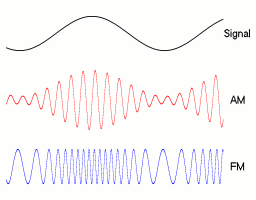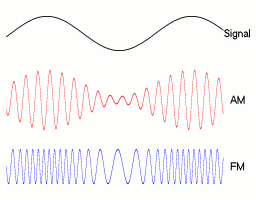
Historical

In the early days of broadcasting, amplitude modulation was the most important method for transmitting signals. There were good reasons to choose AM as the modulation type:

• The main reason was that it was possible to build primitive receivers with obscure and poorly understood tools such as crystal detectors , which are based on the principle of the envelope curve demodulator and only require a few components.
• There was as yet no component or method with which a frequency-modulated signal could be generated or demodulated in the medium wave range.

It was accepted that with AM an unnecessarily large amount of energy has to be invested in the transmission of the "carrier", while only a maximum of 18% of the transmission power is in the information-carrying sidebands. In the USA, methods have therefore been developed to reduce the carrier power when the useful signal amplitude is small in order to save energy. As the number of transmitters and - due to the increased sensitivity of the heterodyne receivers invented in the meantime - the range increased over the years, it became apparent that some properties of AM were very disadvantageous:

• The bandwidth is twice as large as the maximum modulation frequency. In order to be able to assign frequencies in the medium wave range to as many transmitters as possible, a channel grid of 9 kHz was introduced outside of America. The maximum modulation frequency is thereby limited to 4.5 kHz, in practice the AF bandwidth is even limited to 2 to 3 kHz.
• With jammers slightly offset from the grid , AM broadcasts can be effectively disrupted even from a great distance, because annoying interference whistling occurs. This works on shortwave over thousands of kilometers.
• Strictly speaking, an envelope demodulator is a synchronous demodulator that does not generate the required oscillator frequency locally and with very little power, but receives it in the correct phase from the distant transmitter. If selective carrier fading occurs at a great distance , the demodulator delivers an unusable signal.
• Thunderstorms and sparks from passing cars can interfere with AM reception more than any other type of modulation.

Considered from today's state of the art, AM is obsolete because the quality requirements have increased and with modern components, FM devices can be built much simpler, cheaper and more efficient. For reasons of compatibility, AM will probably not be replaced in the medium wave range.

Spectral representation

left: modulation signal as a function of time, right: spectrum of the amplitude-modulated signal

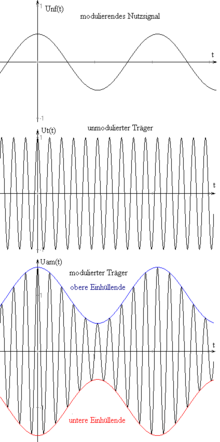
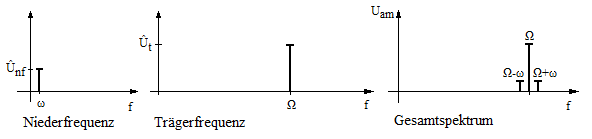
The picture on the right shows the effects of the (low-frequency) modulation signal, the oscillogram of which is shown on the left, on the transmitted frequency spectrum .

By the modulation signal produced symmetrical to the carrier frequency (engl .: Carrier two additional frequencies, the distance indicating the current modulation frequency). Every change is immediately apparent in the position of these accompanying frequencies with respect to the carrier frequency. If the modulation frequency fluctuates between 300 Hz and 4000 Hz, for example, a frequency band with a total width of 8000 Hz is generated. The upper occupied frequency range is called USB ( Upper Side Band ); The lower occupied frequency range is called LSB ( Lower Side Band ).

If the amplitude (" volume ") of the modulation signal changes, the amplitude of the carrier is not influenced, but only the amplitude of the satellite frequencies . In order to reduce this waste of energy in the case of weak modulation, methods were developed in order to then temporarily reduce the strength of the carrier ( dynamic amplitude modulation ).

Application of amplitude modulation

AM is used for:

• Broadcasting on the frequency bands long wave , medium wave , short wave
• FM stereo (with suppressed carrier)
• Television signals of various television standards
• CB radio
• Amateur radio (mostly in a modified form as single sideband modulation )
• Flight navigation (ADF and VOR)
• Aeronautical radio (civil: VHF 117.975 to 137 MHz, military: UHF)
• Chopper amplifier .

Mathematical description

In the following, both the actual frequency f and the angular frequency ω are referred to as frequency. This is possible because both are related via a constant factor . Even so, you have to note that both are still two different sizes. When numbers appear, this is expressed using the units: [ f ] = Hz and [ω] = 1 / s. ${\displaystyle \omega =2\pi \cdot f}$

Fig. 1: Example of amplitude modulation (m = 0.5)

You get a modulated signal when you go to the useful signal

${\displaystyle u_{\mathrm {NF} }={\hat {U}}_{\mathrm {NF} }\cos \omega t}$   (the zero phase angle is assumed to be zero)

a DC component is added and then both with a high frequency carrier wave with multiplied ${\displaystyle {\hat {U}}_{\mathrm {T} }}$ ${\displaystyle \cos \Omega t}$ ${\displaystyle \Omega \gg \omega }$

${\displaystyle u_{\mathrm {AM} }=({\hat {U}}_{\mathrm {T} }+{\hat {U}}_{\mathrm {NF} }\cos \omega t)\ \cos \Omega t}$

${\displaystyle u_{\mathrm {AM} }={\hat {U}}_{\mathrm {T} }\cos \Omega t\ +\ {\hat {U}}_{\mathrm {NF} }\cos \omega t\ \cos \Omega t}$

With the help of the conversion formula

${\displaystyle \cos \alpha \ \cos \beta ={\frac {1}{2}}{\bigl (}\cos(\alpha -\beta )+\cos(\alpha +\beta ){\bigr )}}$

you get:

${\displaystyle u_{\rm {AM}}={\hat {U}}_{\rm {T}}\cos {\Omega t}\ +\ {\frac {{\hat {U}}_{\rm {NF}}}{2}}{\bigl (}\cos {(\Omega -\omega )t}+\cos {(\Omega +\omega )t}{\bigr )}}$

The resulting frequency spectrum can be read from the formula. The modulated signal contains the (constant) carrier signal

${\displaystyle u_{\rm {T}}={\hat {U}}_{\rm {T}}\cos {\Omega t}}$

with the frequency and the amplitude , as well as two sidebands with the frequencies and each with the amplitude . This simplest type of AM modulation is therefore also called double sideband modulation (ZSB or DSB) with carrier. Here the information is in the sidebands, while the carrier itself only represents unnecessary ballast during transmission. When the amplitude of the modulating oscillation changes, the amplitude of the side frequencies also changes. When the frequency of the modulating signal changes, the frequencies of the sidebands also change. ${\displaystyle \ \Omega \ }$ ${\displaystyle {\hat {U}}_{\rm {T}}}$ ${\displaystyle \ \Omega -\omega \ }$ ${\displaystyle \ \Omega +\omega \ }$ ${\displaystyle {\tfrac {1}{2}}\ {\hat {U}}_{\rm {NF}}}$ ${\displaystyle {\hat {U}}_{\rm {NF}}}$

In Figure 1, in addition to the modulated signal, you can also see the two so-called envelopes. These are only used for illustration purposes because their course is the same as the modulating useful signal. Figure 2 shows the three spectra (from the left) of the modulating useful signal, the unmodulated carrier and the modulated signal. As can be seen, the amplitudes of the information-carrying sidebands are significantly smaller than those of the carrier (cf. here the amplitude modulation with suppressed carrier , in which in the ideal case the carrier signal is completely suppressed, ie is). ${\displaystyle {\hat {U}}_{\rm {T}}=0}$

Fig. 2: Spectrum of the amplitude modulation; Degree of modulation m  = 0.5

As an alternative to calculating the modulated signal in the time domain , this can also be done using the Fourier transformation in the frequency domain . The inverse Fourier transformation leads back into the time domain.

Degree of modulation

Fig. 3: Modulation depth and modulation trapezoid in three variants

The degree of modulation indicates how strongly the modulating useful signal influences the amplitude of the modulated (carrier) signal. ${\displaystyle m}$

${\displaystyle m={\frac {{\hat {U}}_{\mathrm {NF} }}{{\hat {U}}_{\mathrm {T} }}}={\frac {U_{\mathrm {AM_{max}} }-{\hat {U}}_{\mathrm {T} }}{{\hat {U}}_{\mathrm {T} }}}={\frac {U_{\mathrm {AM_{max}} }-U_{\mathrm {AM_{\mathrm {min} }} }}{U_{\mathrm {AM_{max}} }+U_{\mathrm {AM_{min}} }}}}$

With results for ${\displaystyle m}$ ${\displaystyle u_{\mathrm {AM} }}$

${\displaystyle u_{\mathrm {AM} }={\hat {U}}_{\mathrm {T} }\left[\cos {\Omega t}\ +\ {\frac {m}{2}}{\bigl (}\cos {(\Omega -\omega )t}+\cos {(\Omega +\omega )t}{\bigr )}\right]}$

It must be greater than 0 and less than or equal to 1 in order to be able to demodulate incoherently. At zero, there is no modulation, only the unmodulated carrier is transmitted. With overmodulation takes place, the resulting signal can only be demodulated coherently without distortion. For this reason, the amplitude of the modulating signal is often limited beforehand in order to avoid excessive modulation . ${\displaystyle m>1}$

Modulation trapezoid

With the modulation trapezoid, the amplitude of the modulated signal (y-axis) is plotted against the amplitude of the modulating signal (x-axis). With sinusoidal signals a trapezoid is created. Depending on how big m is, it can look like a normal trapezoid (0 <  m  <1), like a triangle ( m  = 1) or a fish shape ( m  > 1) (see Figure 3). The formula for m can also easily be determined from the trapezoid .

${\displaystyle m={\frac {B-A}{B+A}}}$

If the phase does not remain constant or there is no pure sinusoidal signal, the modulation trapezoid will be distorted or it may bulge into a cylinder.

Pointer representation

In the pointer representation, the modulation components are plotted as pointers and then (as with the parallelogram of forces ) combined to form the resulting pointer. The two pointers of the sideband _frequencies U _sf1 and U _sf2 , which rotate with the modulation frequency in opposite directions , are located on the rigid carrier U _t . As can be seen in the figures, the x-components of the pointers of the side frequencies are always opposite and therefore cancel each other out when added. All that remains is the sum of the y components, which is added to or subtracted from the carrier amplitude. The resulting instantaneous amplitude of the modulated signal is always in the same direction (in phase) with the carrier amplitude. This is characteristic of double sideband modulation. In the case of amplitude modulation with a suppressed carrier , U _t is missing . In the case of single sideband modulation , either U _sf1 or U _sf2 is also missing . ${\displaystyle \omega }$

Vector representations of the amplitude modulation

The carrier U t in turn rotates with it . ${\displaystyle \Omega }$

Temporal sequence of the pointer display: You can see the alternating constructive and destructive superposition of the carrier and sidebands, which result in the overall signal with its envelope curve (green).

The phasor display shows that the amplitude of a high-frequency overall signal (consisting of the carrier frequency and sidebands) changes with the rhythm of the modulation, but the amplitude of the carrier U _t remains constant. This can be proven either with a spectrum analyzer or by switching on a very narrow band pass (bandwidth <50 Hz) that does not allow the modulation to pass.

Bandwidth

The example was very simple in order to be able to understand the modulation fundamentally. In practice, a low frequency, for example a single tone of constant strength, is modulated onto the carrier. In reality, one modulates significantly more successive frequencies onto the carrier. This amount of frequencies from 0 to is called frequency band or baseband . The areas next to the carrier after modulation are called sidebands . There is an upper (OSB, USB, upper side band) and a lower (USB, LSB, lower side band) sideband; together they form the bandwidth B . ${\displaystyle f_{\rm {i_{\rm {max}}}}}$ ${\displaystyle f_{\rm {B}}}$

${\displaystyle B=2\ f_{\rm {i_{\rm {max}}}}}$

Fig. 7: Amplitude modulation in the spectrum

In broadcasting, a standardized frequency band of 4.5 kHz width (from 0 Hz to 4.5 kHz) is transmitted in the AM range for speech and music, which leads to a bandwidth of B  = 9 kHz. The baseband of the television image signal extends to around 5.5 MHz.

Performance assessment

The actual useful power is in the sidebands, with the same information in both sidebands, which consequently means that a sideband is completely superfluous, as is the carrier. This results in an efficiency . ${\displaystyle \eta }$

${\displaystyle \eta ={\frac {P_{\rm {SB}}}{P_{\rm {ges}}}}={\frac {m^{2}}{4+2m^{2}}}}$

With

${\displaystyle P_{\rm {ges}}=P_{T}+2\ P_{\rm {SB}}}$

${\displaystyle P_{\rm {T}}={\frac {{{\hat {U}}_{\rm {T}}}^{2}}{2R}}}$

${\displaystyle P_{\rm {SB}}={\frac {{{\hat {U}}_{\rm {NF}}}^{2}}{8R}}}$

R is any resistor to which the power is related. Depending on how m is chosen, it is between 0% ( m  = 0) and 17% ( m  = 1). ${\displaystyle \eta }$

Practical implementation of the modulation

Transmitter with amplitude modulation

The useful signal is usually a frequency mix (e.g. speech) that comes from an LF source such as a microphone. The carrier frequency itself is generated with the aid of an oscillator circuit.

The actual modulation takes place in a mixer , for example in a Gilbert cell , in which the useful signal is multiplied by the carrier oscillation. At the output of the mixer after the bandpass filtering , the amplitude-modulated signal is output, which finally reaches the antenna via an RF amplifier .

Basic circuit of an amplitude modulator with a triode

For amplitude modulation in larger transmission systems, for example short-wave transmitters with transmission powers above 100 kW, a water-cooled triode is used in the output stage for modulation, as shown in simplified form in the adjacent circuit diagram. The anode voltage of the triode superimposed with the low-frequency useful signal is obtained from a pulse-step modulator (PSM). The unmodulated carrier frequency (RF) is fed to the control grid of the triode. The amplitude-modulated signal can then be decoupled in the anode circuit and fed to the transmitting antenna via an adjustable pi-filter .

Special types of amplitude modulation

The following modulation variants were developed to save transmission power and / or bandwidth:

• Amplitude modulation with suppressed carrier (DSBSC, double side band suppressed carrier)
• Single side band modulation (SSB)
• Vestigial sideband modulation
• dynamic amplitude modulation

The increased effort involved in demodulation often limits usability.

Digital processes allow low susceptibility to interference or greater use of the spectrum:

• Quadrature Amplitude Modulation (QAM)
• Pulse Amplitude Modulation (PAM).

Demodulation

Coherent demodulation

→ Main article : Synchronous demodulation

At the receiver there is a local carrier that is in phase with the carrier of the received signal. Both are consequently synchronous with each other and therefore coherent. The generation of this local carrier is technically very complex, which is why the method is only used for extremely weak or severely disturbed signals. The mathematical description of the demodulation is quite simple. First, the received signal, consisting of the two side frequencies and the carrier, is multiplied by the local carrier:

${\displaystyle {\begin{aligned}u_{\rm {DAM}}&=u_{\rm {AM}}\ \cos {\Omega t}\\&={\Bigl [}{\hat {U}}_{\rm {T}}\cos {\Omega t}\ +\ {\frac {{\hat {U}}_{\rm {NF}}}{2}}{\bigl (}\cos {(\Omega -\omega )t}+\cos {(\Omega +\omega )t}{\bigr )}{\Bigr ]}\ \cos {\Omega t}\\&={\hat {U}}_{\rm {T}}\cos ^{2}{\Omega t}\ +\ {\frac {{\hat {U}}_{\rm {NF}}}{2}}\left(\cos {(\Omega -\omega )t}\ \cos {\Omega t}+\cos {(\Omega +\omega )t}\ \cos {\Omega t}\right)\end{aligned}}}$

With the help of addition theorems

${\displaystyle \cos \alpha \ \cos \beta ={\frac {1}{2}}{\bigl (}\cos {(\alpha -\beta )}+\cos {(\alpha +\beta )}{\bigr )}}$

${\displaystyle \cos ^{2}\alpha ={\frac {1}{2}}\left(1+\cos {2\alpha }\right)}$

you get:

${\displaystyle {\begin{aligned}u_{\rm {DAM}}={\frac {{\hat {U}}_{\rm {T}}}{2}}\left(1+\cos {2\Omega t}\right)\ +\ {\frac {{\hat {U}}_{\rm {NF}}}{4}}{\bigl (}\cos {(-\omega )t}+\cos {(2\Omega -\omega )t}+\cos {\omega t}+\cos {(2\Omega +\omega )t}{\bigr )}\end{aligned}}}$

Then the undesired high frequency components are filtered out with a low pass and the DC component with a high pass, so that only the wanted signal with half the amplitude remains: ${\displaystyle \ 2\Omega \ }$

${\displaystyle u_{\rm {TP}}={\frac {{\hat {U}}_{\rm {NF}}}{4}}{\bigl (}\cos {(-\omega )t}+\cos {\omega t}{\bigr )}={\frac {{\hat {U}}_{\rm {NF}}}{2}}\cos {\omega t}}$

Incoherent demodulation

→ Main article : envelope demodulator

This simplest form of demodulation does not have to be laborious to generate a local carrier and therefore made it possible to broadcast radio stations a hundred years ago. However, the method can only be used with sufficiently strong signals and generally requires a preceding amplifier. Here, the frequency band sought is filtered out with a band pass, then rectified with a diode and finally smoothed with a low pass . The constant component contained is removed with a high pass if necessary .

${\displaystyle u_{\rm {DAM}}=\left|u_{\rm {AM}}\right|}$

Due to the simplicity of this method, the received signal can easily be disturbed by distortion. The envelope detector and the detector receiver are practical implementations of this process .

See also:

• Grid rectification
• Anode rectification
• Cathode rectification

Multi-level multiplicative demodulation

First, a narrow-band amplification (bandpass) of the desired frequency range ( f _T  -  f _{i max} to f _T  +  f _{i max} ) is carried out with a slightly damped resonant circuit that can be tuned to the carrier frequency f _T. Then, depending on the technology available, the modulation to lower frequencies is carried out in n steps. So a modulator per stage followed by a low pass .

As with the transmitter, the modulator itself is a multiplier. In this example there is only one ( n  = 1) modulator for the sake of simplicity . The carrier frequency in the receiver f _Te required for the modulator should correspond as closely as possible to the carrier frequency of the transmitter f _T , since otherwise a beat occurs. The readjustment of f _Te takes place nowadays via a PLL (phase locked loop).

Result of the transmitter: f _m1 = 220 kHz and f _m2 = −240 kHz; f _T = 230 kHz
(phase shown above sign)

In the receiver under the condition f _T  = f _Te :

${\displaystyle f_{0}=f_{m1}\pm f_{Te}}$   and     (phase and amplitude omitted) ${\displaystyle f_{0}=f_{m2}\pm f_{Te}}$

from which the frequencies result with the above information: −10 kHz; 450 kHz; −10 kHz; −470 kHz

All frequencies above 10 kHz can now be filtered out with a low pass.

In the real case it is hardly possible to hit the carrier frequency of the transmitter with sufficient accuracy. To get an idea of ​​the required accuracy, here is an example: A beat of 50 Hz corresponds to a frequency deviation of 0.02% based on 230 kHz.

In order to avoid as many problems as possible in analog technology (has to be adjusted, electronic components age) and to minimize space requirements, digital signal processing is increasingly being used. In principle, the received signal is digitized directly into sine and cosine components with a fast analog-digital converter . The rest is done mathematically by the signal processor .

Abbreviations

• A1: amplitude keying
• A2: sounding telegraphy
• A3: amplitude-modulated transmission of analog signals (e.g. speech and music)

Amplitude modulation in electromagnetic compatibility

In the area of electromagnetic compatibility , amplitude-modulated signals are often used as interference signals in immunity tests. Two different references to the corresponding unmodulated signal are used here. If the reference level of the modulated signal is fixed at its peak value , one speaks of downward modulation . If, on the other hand, the reference level is set at the zero crossing of the modulated low-frequency useful signal, then one speaks of upward modulation . A sine tone with 1 kHz is used as the useful signal , in rare cases alternatively with 400 Hz or 1 Hz. The degree of modulation of the interference signal is usually 80%, which means that the peak value of an up-modulated interference signal is 1.8 times the reference level.

In tests according to the basic standards EN 61000-4-3 or EN 61000-4-6 (immunity to radiated or conducted electromagnetic fields), upward-modulated interference signals are used.

In tests according to ISO 11451 or ISO 11452 (road vehicles - electrical interference from narrow-band radiated electromagnetic energy, road vehicles or components), downward-modulated interference signals.

However, above 800 MHz, pulse-modulated interference signals are generally used in the range of the two ISO standards , whereby the same peak value of the interference signal is achieved with both types of modulation due to the AM downward modulation.

See also

• Frequency modulation

Web links

Commons : Amplitude Modulation  - collection of images, videos and audio files

Wiktionary: amplitude modulation  - explanations of meanings, word origins, synonyms, translations

• Overview of modulation methods ( PDF ; 186 kB)
• Overview of modulation methods ( PDF ; 328 kB)
• Amplitude modulation ( PDF ; 1.83 MB)
• Modulation and Noise ( PDF ; 642 kB)

Individual evidence

1. ↑ AM - amplitude modulation. Retrieved February 14, 2020 .