Beat

As beat is referred to the effect that the resultant of the additive superposition ( superposition ) of two oscillations , which differ in their frequency only slightly different from each other, a periodically increasing and decreasing amplitude has.

Beatings occur with waves for which the superposition principle applies, for example with sound waves , electromagnetic waves or electrical signal currents. Since the instantaneous values ​​of the output oscillations periodically strengthen or weaken each other depending on the phase position , the resultant has an increasing and decreasing amplitude. The frequency of this change is higher, the greater the difference between the output frequencies and is. ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$

In contrast to the methods used in mixer stages , no new frequencies are generated with beating , and no frequency shifts occur either.

Frequency and period

Example of a beat of two frequencies.
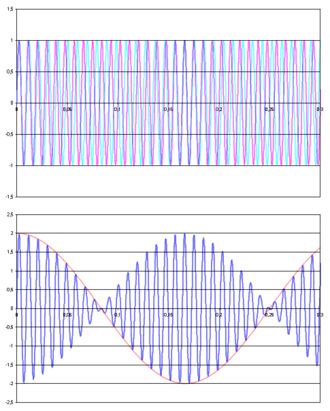
Above the two signal frequencies and in the colors cyan and magenta . Below the beat, formed by adding the two above curves. The frequency of the blue curve results as the mean value of the two frequencies, the frequency of the envelope curve (red) results as half the difference between the two frequencies. ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$

Two harmonic oscillations and with slightly different frequencies and : ${\displaystyle y_{1}}$ ${\displaystyle y_{2}}$ ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$

${\displaystyle y_{1}(t)={\hat {y}}_{1}\sin(2\pi f_{1}t)}$

${\displaystyle y_{2}(t)={\hat {y}}_{2}\sin(2\pi f_{2}t)}$

For the sake of simplicity it is assumed that both oscillations have the same amplitude.

${\displaystyle {\hat {y}}_{1}={\hat {y}}_{2}={\hat {y}}}$

Then the total oscillation (beat function) can be represented as follows (index for resultant ): ${\displaystyle _{\mathrm {R} }}$

${\displaystyle y_{\mathrm {R} }\left(t\right)={\hat {y}}\left(\sin \left(2\pi f_{1}t\right)+\sin \left(2\pi f_{2}t\right)\right)}$

This expression can be transformed by applying the trigonometric addition theorems :

${\displaystyle y_{\mathrm {R} }\left(t\right)=2{\hat {y}}\cdot \sin \!\left(2\pi \left({\frac {f_{1}+f_{2}}{2}}\right)t\right)\cdot \cos \!\left(2\pi \left({\frac {f_{1}-f_{2}}{2}}\right)t\right)}$

This expression can be simplified with the following definitions:

${\displaystyle f_{\mathrm {R} }={\frac {f_{1}+f_{2}}{2}}}$: Frequency of the superposition oscillation ( mean value of the individual frequencies)

${\displaystyle f_{\mathrm {S} }={\frac {|f_{1}-f_{2}|}{2}}}$: Frequency of the envelope

${\displaystyle \Rightarrow y_{\mathrm {R} }\left(t\right)=2{\hat {y}}\cdot \sin \!\left(2\pi f_{\mathrm {R} }\,t\right)\cdot \cos \!\left(2\pi f_{\mathrm {S} }\,t\right)}$

The beat frequency results from the course of the amount of the envelope:

${\displaystyle f_{\mathrm {Schwebung} }=\left|f_{1}-f_{2}\right|=2\,f_{\mathrm {S} }\ll f_{\mathrm {R} }}$

${\displaystyle \Rightarrow y_{\mathrm {R} }\left(t\right)=2{\hat {y}}\cdot \sin \!\left(2\pi f_{\mathrm {R} }\,t\right)\cdot \cos \!\left(\pi f_{\mathrm {Schwebung} }\,t\right)}$

The beat period

${\displaystyle T_{\mathrm {Schwebung} }={\frac {1}{f_{\mathrm {Schwebung} }}}}$

is the time between two points of minimum amplitude ( nodes ) of the beat function. The beat period is greater, the closer the two output frequencies and are together. ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$

If the amplitudes and the two frequencies are not the same, then one speaks of an impure beat . ${\displaystyle {\hat {y}}_{1}}$ ${\displaystyle {\hat {y}}_{2}}$

Acoustic beats

The beating can be clearly heard in the acoustics : If two tones are heard whose frequencies differ only slightly, a tone can be heard whose frequency corresponds to the mean value of the frequencies of the two superimposed tones. This tone is modulated , its volume fluctuates with the above. Beat frequency, which corresponds to the difference between the frequencies of the two tones.

If the frequency difference increases, the ear is no longer able to follow the ever-increasing fluctuations in volume, and one hears a tone with a rough tone that splits into two individual tones when the frequency difference increases further. If the beat frequency exceeds the hearing threshold of approx. 20 Hz, it becomes audible as a difference tone .

This phenomenon is demonstrated by the following sound example ^{? / i} : A sine tone with a constant frequency of 440 Hertz is superimposed on a second sine tone, the frequency of which increases from 440 Hertz to 490 Hertz.

How the beats of an interval (here a semitone ) are perceived depends very much on the altitude , which becomes clear in the following example:

Example : The (sine) tones e and f from the major to the three- stroke octave are played first individually, then together. The frequency of f is 6.6% higher than that of e in each octave.

in Hz

E 82.5

F 88

EF

e 165

f 176

ef

e '330

f '352

e 'f'

e & quot; 660

f '' 704

e '' f ''

e '' '1320

f '' '1408

e '' 'f' ''

alone

alone

together

alone

alone

together

alone

alone

together

alone

alone

together

alone

alone

together

Sound samples

Beats when two tones are superimposed at 440 Hz and 440.5 Hz

With pure sine waves

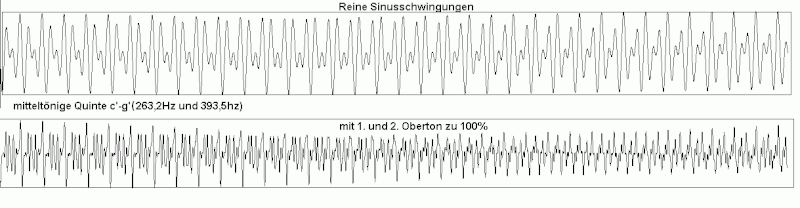
With 100% basic frequency , 50% first overtone and 25% second overtone

Two chromatic semitones (frequency difference 4%) in harmony

Pure sine tones: The beat character is clear when they are played together. Hardly two separate tones audible.

As an organ register with overtones (fundamental: 100%, overtones: 75%, 50%, 30%, 15%, 10% and 5%). Here you can clearly hear two separate tones when they sound together (you can sing them afterwards).

With special waveforms

In order to make it easier to understand the acoustic beats, there are four examples here, which differ in their waveform :

• Triangular oscillation
• Square wave
• Sawtooth oscillation
• Sine wave

In all four sound samples, two vibrations were superimposed, which initially have the same starting frequency of 110 Hz. After 4 seconds, the frequency of one oscillation is gradually increased (in 8 seconds by 50  cents ), then it remains the same for 6 seconds, is now reduced by 100 cents more quickly than in the increase, and after another stable phase it increases again at −50 cents the output frequency changed. The following diagram shows the exact course:

Frequency curve of the variable oscillation from the above four examples. The constant oscillation (not shown) lies on the zero line. The deviation of the frequency of the second oscillation from the 110 Hz of the first oscillation is plotted in the vertical direction, in cents.

At impure intervals

In the case of imprecisely voiced intervals, the beats of the overtones can be calculated as follows:

Octave: ${\displaystyle f_{\mathrm {Schwebung} }=\left|2\cdot f_{1}-f_{2}\right|}$

Fifth : ${\displaystyle f_{\mathrm {Schwebung} }=\left|3\cdot f_{1}-2\cdot f_{2}\right|}$

An example of this in a mean- tone tuning : mean- tone fifths

major third : ${\displaystyle f_{\mathrm {Schwebung} }=\left|5\cdot f_{1}-4\cdot f_{2}\right|}$

At the intervals, which are usually outside the critical range, a beat can be heard when two clearly present overtones or an overtone and a fundamental frequency are close together.

As you can see from the following wave pictures, a beat is hardly perceptible with pure sine tones (the amplitudes hardly change), but with a high overtone component it is clearly audible:

Example: mean-tone fifth. First pure sine waves, then with overtones

Beatings at intervals play a major role in the pure , the mid-tone , the well-tempered and the equal temperament . For example, with a pure third one does not hear any, but with the same step a significant beat - felt as friction -. The beats of the mid-tone fifths are so small that they are not perceived as a dissonance.

Acoustic illusion?

The auditory perception of beats is generally not based on an acoustic illusion , but on real physical processes. This is different with binaural beats , where the ears are fed one of two different frequencies via headphones and the perception of beats only arises through signal processing in the brain.

Applications

The phenomenon of beating can be applied in many ways, e.g. B. in music making practice:

• The tuning of a musical instrument by ear (without a tuner with visual display), i.e. the actual tuning to the concert pitch as a reference frequency , takes place until no more beats can be heard: the tone is then "beat zero - it is correct".
• The beat is used as an invigorating sound effect on musical instruments , for example as a switchable tremolo effect or as a special register in pipe organs .
• With the tremolo harmonica ( Viennese tuning ) and most hand-drawn instruments , the sound is generated with two reeds that are tuned in one beat .
• The tone harmony of the bamboo instrument Angklung is based on the principle of two to four vibrating bodies of sound ( bass , melody instruments and chords ) that are shaken at the same time.
• The Leslie loudspeaker cabinet uses the Doppler effect to generate periodically fluctuating frequencies. When the original sound is superimposed , a beat is created.

In metrology , an electronically measurable beat is generated by superimposing laser light of an only roughly known frequency with a frequency comb , which enables a much more precise determination of the frequency of the laser.

The beating becomes unpleasantly annoying when two instruments with approximately sinusoidal tones (e.g. flutes ) play closely adjacent tones - it is said that the tones “rub”. When two recorder beginners play in unison, extreme imperfections can even result in an extremely penetrating difference tone being audible in the depths.

literature

• Dieter Meschede (Ed.): Gerthsen Physik . 22., completely reworked. Edition. Springer, Berlin a. a. 2004, ISBN 3-540-02622-3 .

Web links

• Simulation of interference / beat / Lissajous_Kurven of two standing waves