Combination tone

Combination tones can arise when two different tones sound at the same time by forming differences or sums from the two basic frequencies (or their multiples).

Combination tones have occasionally been the subject of music theory , e.g. B. in Hindemith's instruction in composition .

discovery

Combination tones, known at the time as difference tones, were discovered by Giuseppe Tartini in 1714 , described in 1744 in the "Instructions for Mood and Temperature" by Georg Andreas Sorge and examined in more detail by Giuseppe Tartini in 1754, later by Thomas Young , Röber and Hermann von Helmholtz . With the help of theory, the latter has also discovered a higher tone analogous to the difference tone, whose number of vibrations corresponds to the sum of the numbers of vibrations of the exciting tones ( summation tone ).

Difference tones

Those combination tones, the frequencies of which result from the formation of the difference from the primary frequencies or their multiples, are called difference tones or also Tartini tones, after the Italian violinist Giuseppe Tartini , who heard them when he played double stops on his violin.

The best-known and most easily audible difference tone is the "square" difference tone. Its frequency corresponds to the beat frequency, i.e. the difference between the fundamental frequencies of the two output tones: ${\displaystyle f_{D}}$

${\displaystyle f_{D}=f_{2}-f_{1}}$

With

• f ₂ : frequency of the higher tone
• f ₁ : frequency of the lower tone .

Example:

Pure sine tones. Listen ? / i

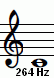
This combination tone can be heard at a high volume. Listen ? / i

Trained musicians hear further differences and sums of the multiples of the output frequencies as combination tones.

In organ building , an acoustic phenomenon is incorrectly called a difference tone. Actually, these are residual tones ; see also acoustic illusion .

Formed in the ear

→ Main article : Distortion-produced otoacoustic emissions

If two primary tones with frequencies f ₁ < f _{2 are} presented to an observer , the square difference tone f ₂ - f ₁ and the cubic difference tone 2 ×  f ₁ - f ₂ arise in the ear . Under suitable conditions, however, higher order difference tones can also be perceived.

Square difference tones formed in the ear behave like regular distortions; H. as the sound level of the primary tones rises, so does the level of the square difference tone.

According to Eberhard Zwicker, however , the cubic difference tones formed in the ear show an “unusual amplitude response ”. As the level of the higher primary tone increases, the level of the cubic difference tone initially increases, as is to be expected with regular distortions. However, if the level of the higher primary tone exceeds the level of the lower primary tone, the level of the cubic difference tone decreases again.

It can be seen from numerous measurement results that the difference tones generated in the ear behave in principle in the same way as tones supplied to the ear from outside. The peripheral part of the hearing is therefore assumed to be the origin of the difference tones.

observation

Inexperienced people often find it difficult to distinguish the existing tones from the combination tones. If a constant tone of frequency f _{1 is} generated and a tone of increasing frequency f _{2 is} superimposed on it , the observation is easier: In addition to frequency f ₁ and the increasing frequency f ₂ , at high volume one can hear the square combination tone of frequency f ₂ - f ₁ and even quieter the cubic combination tone with the frequency 2 ×  f ₁ - f ₂ .

Audio sample

Two tones are played with the frequencies and (in Hz): ${\displaystyle f_{1}\!}$ ${\displaystyle f_{2}\!}$

${\displaystyle f_{1}\!}$	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440
${\displaystyle f_{2}\!}$	440	466	494	523	554	587	622	659	698	740	784	831	880	932	988	1047	1109	1175	1245	1319	1397	1480	1568	1661	1760
Listen ? / i

If you play this out loud, you will hear the square and even quieter the cubic difference tones.

In the following example, the square combination tones are amplified with the frequencies for clarity . (The square combination tone can be heard ascending from the depth.) ${\displaystyle f_{2}-f_{1}\!}$

${\displaystyle f_{1}\!}$	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440
${\displaystyle f_{2}\!}$	440	466	494	523	554	587	622	659	698	740	784	831	880	932	988	1047	1109	1175	1245	1319	1397	1480	1568	1661	1760
${\displaystyle f_{2}-f_{1}\!}$	0	26th	54	83	114	147	182	219	258	300	344	391	440	492	548	607	669	735	805	879	957	1040	1128	1221	1320
Listen ? / i

In the following example, the cubic combination tones are amplified with the frequencies for clarity . (You can hear the cubic combination tone first descending and then ascending again.) ${\displaystyle |2\cdot f_{1}-f_{2}|}$

${\displaystyle f_{1}\!}$	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440
${\displaystyle f_{2}\!}$	440	466	494	523	554	587	622	659	698	740	784	831	880	932	988	1047	1109	1175	1245	1319	1397	1480	1568	1661	1760
${\displaystyle |2\cdot f_{1}-f_{2}|}$	440	414	386	357	326	293	258	221	182	140	96	49	0	52	108	167	229	295	365	439	517	600	688	781	880
Listen ? / i

causes

The superposition of two oscillations (z. B. 1200 and 1300 Hertz) is given by the effect of the beat an amplitude-modulated and audible vibration with a modulation frequency equal to the difference tone (100 Hertz).

Especially at frequencies above 1600  Hertz , the human hearing can no longer record the exact time function of the sound signals, but only their envelope curve . The evaluation results in an oscillation with the frequency of the difference tone.

Furthermore, non-linear distortions in the sound source itself, i.e. the sound transducer , the instrument or in the ear, can also play a role.

Consequences for musicians

Musicians make use of the effect of the combination tones when tuning instruments in which the tone generators (e.g. strings , whistles ) are to be tuned at a distance of a perfect fifth . The difference tone then sounds exactly one octave below the lower tone generator.

The phenomenon of “combination tone” also has consequences for music theory. If one compares the major third in pure tuning and in equal tuning , one notices a roughness in equal tuning , which is intensified by the difference tone. In the case of the pure major third, the difference tone is exactly two octaves below the lower tone, whereas in the case of the equal pitch it is a semitone higher, which results in a dissonance with the interval sound .

at first only c ″ e ″ (frequencies 528 Hz and 660 Hz) then with difference tone C (132 Hz) Listen ? / i

equal at first only c ″ e ″ (frequencies 528 Hz and 665.24 Hz) then with difference tone C sharp (137.24 Hz) Listen ? / i

See also

• Ring modulator
• Two-tone excitation

literature

• Angela Lohri: Combination tones and Tartini's »terzo suono« Verlag Schott Campus 2016, ISBN 978-3-95983-080-5 Print version and PDF download
• Eberhard Zwicker: The unusual amplitude response of the non-linear distortions of the ear. In: Acustica. 5, 1955, ISSN  0001-7884 , pp. 67-74.
• Adrian Wehlte: Trios for two (trios with 2 flutes and combination tone , explanations and practical exercises for pure intonation) Tibia Heft 2/2012 Moeck-Verlag , Celle 2012, ISSN  0176-6511 and practice books

References and comments

1. ↑ De 'Principj dell'armonia musicale contenuta nel diatonico genere. Dissertazione. Padua 1767 , in it on p. 36: "Nell'anno 1714, giovine di anni 22, incirca scopre fortunatamente sul violino questo fenomeno in Ancona, dove non pochi ricordevoli testimonj sopravvivono ancora."
2. ↑ Instructions for the tuning and temperature of both the organ works and other instruments, especially the piano, digitized p. 41
3. ↑ Oliver Lehrbaß: auditory physiology and otoacoustic emissions. 2007, ISBN 978-3-638-79771-9 , p. 82. (online)
4. ↑ With Hermann von Helmholtz you can read about the fact that the tuning of the same level - called equal floating by him - differs almost inaudibly from the Pythagorean tuning. P. 508 “These bad combination tones [meaning the thirds] have always been the most agonizing thing for me in the harmony of the equal temperament [...] form a hideous basic bass.” P. 510 “The main flaw in our current tempered mood is not in the Fifths; because their impurity is not worth mentioning […] The mistake lies in the thirds. ”Ross W. Duffin writes (freely translated and summarized): p. 27 In the case of equal tuning, the fifths are adjusted (instead of 702 cents just 700 Cent) [...] and that ends the story for many writers and musicians - except that this system of 12 equal semitones simplifies the musical harmony in a terrible way. Because many musicians today do not notice how terrible the major third sounds in equal tuning (there the deviation is 14 cents, a seventh semitone). This interval is the invisible elephant in our system. Swell:
   • Hermann von Helmholtz: The theory of tone sensations as a physiological basis for the theory of music . Vieweg, Braunschweig 1863, reprint: Minerva-Verlag, Frankfurt / Main 1981, ISBN 3-8102-0715-2 Excerpt ( memento of the original from July 13, 2015 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. 
   • Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You Should Care). WW Norton & Company, New York / London 2007 (excerpt) ( Memento of the original from March 16, 2015 in the Internet Archive ) Info: The archive link has been inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. 
5. ↑ Strictly speaking, C sharp has a frequency of 137.5 Hz, with the frequency ratios ^C ⁄ _A = ¹³² ⁄ ₁₁₀ = ⁶ ⁄ ₅ (minor third) and ^{C sharp} ⁄ _A = ^137.5 ⁄ ₁₁₀ = ⁵ ⁄ ₄ (major third) becomes. The difference between 137.5 Hz and 137.24 Hz is only 3  cents , so negligible.