Instruction in composition

This article or the following section is not adequately provided with supporting documents ( e.g. individual evidence ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and including good evidence.

Instruction in music theory is the title of music theory and tonsatzpraktischen textbook by Paul Hindemith . It consists of three parts:

• I. Theoretical part . Schott, Mainz 1937.
• II. Exercise book for the two-part movement . Schott, Mainz 1939.
• III. Exercise book for the three-part movement . Schott, Mainz 1970.

With this work, Hindemith's main aim is to end the technical chaos that he believes is rampant in contemporary music and to put the compositional craft back on a solid theoretical basis. He would like to replace the outdated and unsuitable teaching system of traditional harmony with something new and contemporary. In addition, Hindemith evidently endeavors to counter the twelve-tone technique of Schönberg , which he heavily criticized, with an alternative system on a tonal basis.

Theoretical part

The main innovations in Hindemith's theory are:

• an alternative derivation of the chromatic scale as the basis of a free tonality .
• a new chord theory as a replacement for traditional harmony theory .
• the innovative attempt at teaching melody.

row 1

Criticism of the previous scale systems

Hindemith describes the equally tempered tuning as "one of the most ingenious inventions of the human mind" and appreciates its inestimable practical value for keyboard instruments, but at the same time limits the fact that it is not safe to offer the ear only music in tempered intervals, otherwise it would be get used to the constantly clouded sound and the sense of pure sounds is lost. "Fortunately, however, the instrumental and singing voices capable of pure intervals form the main power over the keyboard instruments and it is hardly to be assumed that the musical sensation could ever sink so far that the keyboard instruments can gain exclusive control."

In the chapter “Earlier attempts at scales” Hindemith deals with, among other things, the Pythagorean and mean-tone tuning and comes to the conclusion that all these systems are “not an original creation of a scale. Here one starts from a scale model that is already available in practical music and tries to justify the scale intervals that have proven useful through experience. "

That is why Hindemith takes "a third way of calculating the scale [...] which will lead us to goals that have not been achieved in the above-mentioned ways."

New derivation of the chromatic scale

Hindemith performs his derivation of the chromatic scale using the example of the capital C with 64 Hz as the starting tone . The derivation process is a kind of journey of discovery in the area of ​​the overtone series of this C, with a restriction to the first six partials. As Hindemith explains in detail, the inclusion of the seventh and higher overtones would lead to useless, even chaotic results.

The starting material is therefore the notes C, c, g, c ₁ , e ₁ , g ₁ .

The goal is now to fill the octave space above the C with tones in such a way that a musically usable tone scale is created. For this purpose, the realm of overtones is systematically explored and every new “discovery” is incorporated into the tone stock. The practical procedure consists in applying the ratios of the previous partials known up to that point to each new overtone. The new overtone in each case is thought of as the first, second, etc. overtone of a row below, the fundamental tone of which then results in a new tone that fits into the scale.

• The application to the second overtone of C (64 Hz), the C with 128 Hz means that this can function as the first or second overtone (the third overtone will only be discovered later). In its role as the first overtone, it only refers to itself as the fundamental; as the second overtone, it only delivers the existing C with 64 Hz.
• Only the third overtone, the G with 192 Hz, produces something new: It is not usable as the first overtone because it lies outside the octave to be filled, but as the second overtone it creates the new scale tone G (96 Hz).
• The fourth overtone, the c ₁ (256 Hz) provides the F with 85.33 Hz in the role of a third overtone .
• The fifth overtone, the e ₁ (320 Hz) - intended as the third overtone - provides the fundamental A (106.66 Hz).
• Made the fourth overtone, the e ₁ (320 Hz) refers to the fundamental E (80 Hz).
• The sixth overtone, the g ₁ 384 Hz, provides the role of a fifth harmonic of the time (76.8 Hz).
• As an extension of the previous procedure, the fourth overtone of C, the c ₁ (256 Hz), is made a fifth and leads to an A-flat ₁ , the second overtone A- flat (102.4 Hz) of which is recorded.

This means that “the power of the original note C [...] is exhausted,” says Hindemith. "The tones c, G, F, A, E, Es, As, developed from him, surround him like a proud number of sons. [...] They can [...] set up their own household while they are still in paternal care and can please their producer with a bevy of grandchildren. "

The "sons" are now subjected to the same procedure in the order of their "birth" as the progenitor C, that is, their overtones are used to obtain new scale tones. While Hindemith discusses all cases in detail, only those are mentioned here which lead to new results.

• The third overtone of G, which delivers d ₁ at 288 Hz - made the 4th overtone in a series - its fundamental D (72 Hz).
• The fourth overtone of the F, the f ₁ with 341.33 Hz leads to the B (113.78 Hz) in the role of a third overtone .
• The same f ₁ refers as the fifth overtone of the fundamental tone Des (68.27 Hz)
• The third overtone of E - intended as the second overtone - provides the B (120 Hz)

"The family will be complete when we include C's great-grandchildren."

• A G flat (91.02) is obtained from the “grandson” of Db by making a third overtone from the fourth overtone of Db , that of ₁ with 273.08 Hz.
• The fifth overtone of the "grandson" D, the F sharp ₁ delivers the F sharp (90 Hz) as the fourth overtone , one oscillation lower than the Ges.

Hindemith calls the notes arranged in the order in which they were discovered as row 1 .

Row 1 as a table

volume

C.

G

F.

A.

E.

It

As

D.

B.

Of

H

Ges / Fis

Frequency (Hz)

64

96

85.33

106.66

80

76.8

102.4

72

113.78

68.27

120

91.02 / 90

Kinship relationship

father

Sons

grandson

Great-grandchildren

Meaning of row 1

Hindemith himself must have seen the discovery of series 1 as an achievement whose historical significance is comparable to the invention of the well-tempered tuning . Because similar to how Bach realized the tempered tuning in his Well-Tempered Clavier , Hindemith does this with his series 1 by using it as the basis for the piano cycle Ludus tonalis .

The parallel would be even more convincing if the Ludus tonalis could be performed on a piano that was tuned to the frequency relationships of row 1 . This is forbidden, however, since row 1 would be completely unsuitable as a basis for the tuning of a piano, as becomes immediately clear when one examines the frequency relationships of the fifths occurring between their tones. Most fifths are pure, so they have the frequency ratio 3: 2 = 1.5. The fifths DA and Eb-B, however, have a frequency ratio of approx. 1.48 (≈ 678 cents ), so they are so-called wolf fifths .

Even if the purely practical use of row 1 is consequently small, from Hindemith's point of view its theoretical meaning consists in the fact that the chromatic scale no longer appears as an extension of the diatonic scales, but as a natural product that is just as easy to derive “Can be understood. Hindemith even claims that it “proves to be the most natural of all scales, which is also the most suitable for melodic and harmonic work.” As such, it forms the basis of a free tonality that is no longer based on the conventional major-minor system is limited.

Row 2

Row 1 describes a ranking of decreasing relationship between the individual chromatic tones and a central tone. In contrast to this, row 2 refers to a gradation of the sound value of the intervals .

Combination tones

In order to determine the sound value of the intervals, Hindemith relies on the acoustic phenomenon of the combination tones . These are physically real tones that can also be heard when two (or more) tones sound together. When two tones sound together, a difference tone occurs, the frequency of which corresponds to the difference between the output tone frequencies:, where the frequency of the higher tone means the frequency of the lower tone. This difference tone in turn interacts with the already sounding interval tones and so on, so that theoretically an infinite number of combination tones occurs, which, however, become weaker the higher their order. Hindemith therefore restricts himself to considering the combination tones of the first and second order. ${\displaystyle f_{D}=f_{2}-f_{1}\,}$ ${\displaystyle f_{2}\,}$ ${\displaystyle f_{1}\,}$

To clarify the terms, the following precise definition should be added:

Combination tone 1st order = difference tone D ₁ with . ${\displaystyle f_{D_{1}}=f_{2}-f_{1}\,}$

2nd order combination tone = difference tone D ₂ with . ${\displaystyle f_{D_{2}}=f_{1}-f_{D_{1}}=2f_{1}-f_{2}\,}$

(The 2nd order combination tone relevant here arises from the interaction of the first difference tone with the lower tone of the sounding interval. The interaction with the upper tone does not result in a new tone, because this tone would be identical to the already sounding lower tone of the interval. ) ${\displaystyle f_{D_{2}}=f_{2}-f_{D_{1}}=f_{1}\,}$

The following table shows these ratios for the simplest intervals. The frequencies are each reduced (by shortening) to the smallest possible integer values.

interval	${\displaystyle f_{2}\!}$	${\displaystyle f_{1}\!}$	${\displaystyle D_{1}\!}$	${\displaystyle D_{1}\!}$ is so	${\displaystyle D_{2}\!}$	${\displaystyle D_{2}\!}$ is so	Conclusion
octave	2	1	1	${\displaystyle =f_{1}\!}$	0	inaudible	${\displaystyle f_{1}\!}$ is amplified
Fifth	3	2	1	1 octave lower than ${\displaystyle f_{1}\!}$	1	1 octave lower than ${\displaystyle f_{1}\!}$	${\displaystyle f_{1}\!}$ is supported twice
Fourth	4th	3	1	2 octaves lower than ${\displaystyle f_{2}\!}$	2	1 octave lower than ${\displaystyle f_{2}\!}$	${\displaystyle f_{2}\!}$ is supported twice
major third	5	4th	1	2 octaves lower than ${\displaystyle f_{1}\!}$	3	1 quart deeper than ${\displaystyle f_{1}\!}$	${\displaystyle f_{1}\!}$ is simply supported
little sext	8th	5	3	great sext under ${\displaystyle f_{1}\!}$	2	2 octaves lower than ${\displaystyle f_{2}\!}$	${\displaystyle f_{2}\!}$ is simply supported
minor third	6th	5	1	2 octaves + major third below ${\displaystyle f_{1}\!}$	4th	major third under ${\displaystyle f_{1}\!}$	none of the interval tones are supported
great sext	5	3	2	1 quint lower than ${\displaystyle f_{1}\!}$	1	1 octave + fifth lower than ${\displaystyle f_{1}\!}$	none of the interval tones are supported

In this table the intervals are already arranged in such a way that the cloudiness or exposure to combination tones increases from top to bottom. One can also speak of a gradually decreasing degree of consonance .

Interval fundamental tones

As a result of the reinforcement by combination tones, one of the two interval tones gains the upper hand and thus becomes the fundamental tone. For fifths and major thirds the root note is below, for fourths and minor sixths it is above. The fifth and fourth as well as third and sixth thus form pairs, with one partner being the inverse of the other.

With a minor third and major sixth, however, neither of the two interval tones is amplified by the combination tones, so that, strictly speaking, the assumption of a fundamental tone is prohibited. For the practical reason of simplification and ease of use, Hindemith disregards the strict theoretical requirement and assigns the minor third the lower note and the major sixth the upper note as the fundamental tone.

He proceeds in a similar way with the seconds and sevenths, for which no clear fundamental tones can be identified either. Here, too, Hindemith distributes the (fictitious) basic tones according to purely pragmatic points of view.

The tritone occupies a special position . Its combination tones depend on which of its various shapes you are looking at.

Tritone	narrow shape	wide shape	D 1 = difference tone with (combination tone 1st order) ${\displaystyle f_{D_{1}}=f_{2}-f_{1}\,}$ D 2 = difference tone with (2nd order combination tone) ${\displaystyle f_{D_{2}}=f_{1}-f_{D_{1}}\,}$ In the narrow form is produced with As - it c 1  - ges 1 as overall sound a dominant , with resolution effort to Des-Dur, while when the wide form with A - d - c 1  - fis 1 a reversal of belonging to G major dominant seventh arises. This shows that there is always a tension in the tritone that urges dissolution.
Sounds	c 1   ges 1	c 1   f sharp 1
Frequency- relationship	5: 7	7:10
D 1	As	d
D 2	it	A.

Row 2 as a table

interval	octave	Fifth	Fourth	major third	little sext	minor third	great sext	great second	small Sept	small seconds	great Sept	Tritone
upper tone	c 1	G	c 1	e	c 1	it	c 1	d	c 1	of	c 1	f sharp
lower tone	c	c	G	c	e	c	it	c	d	c	of	c
Keynote	both	c	c 1	c	c 1	c	c 1	d	d	of	of	none

With the tritone, one of its two tones is occasionally declared to be the substitute root note , namely the one that leads into the root note of the dissolution interval. Example: The tritone e - b is resolved into the third f - a. Then the e is the substitute root because it leads to the f as the root of the resolution interval.

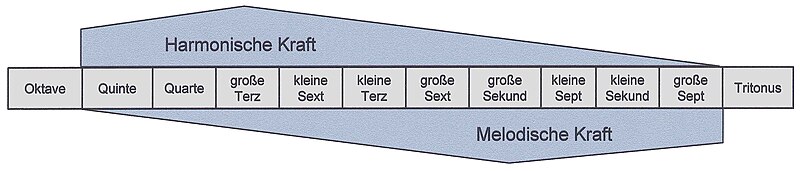
Harmonic and melodic value of the intervals

Row 2 also reflects the different harmonic and melodic value of the intervals. Octave (as hardly differentiated from harmony) and tritone (as iridescent in its effect and meaning) are isolated on the left and right edge. For the other intervals, there is a quasi-complementary ranking with regard to their harmonic or melodic usability. However, Hindemith deviates from a strictly systematic assessment in that he describes not the small but the large second as the “most beautiful” melodic interval. Accordingly, he does not consider the perfect (but also empty!) Fifth to be the “most beautiful” harmonic interval, but rather the major third and justifies this with its greater color as a result of the chord effect of its combination tones.

Chord theory

Critique of the traditional theory of harmony

Hindemith criticizes four points of traditional harmony theory, which make it appear “too narrow a system of sound determination and processing:

1. The construction principle of the sounds is the layering of thirds.
2. The sounds are reversible.
3. The chord supply of a key can be expanded by increasing or deepening the individual notes of the diatonic ladder.
4. The chords are ambiguous. "

Chord determination

According to Hindemith, a new system of determining chords must meet the following requirements:

1. No longer just thirds, but any intervals can be used to build the chords.
2. In place of the chord inversions, a more comprehensive principle must appear.
3. The ambiguity of the chords must be eliminated.

This means that any combination of at least three tones (two tones only form an interval) must be viewed as a chord. A distinction is possible on the basis of the degree of dissonance, which results from the intervals contained. According to Hindemith, whether or not they contain a tritone also plays an important role in the classification of the chords. Tritone chords require special treatment because of the tension inherent in them. Instead of the traditional distinction between the basic position and inversions, there is a distinction between chords whose root is identical to the bass note and those whose root is higher in the chord. To determine the chord root, the root of the most consonant interval contained in the chord is used (ignoring the octave). So if z. B. If a fifth occurs in the chord, its lowest note is declared to be the chord root. Using these criteria, Hindemith comes to the following classification of the chords:

Chord definition table

A sounds without a tritone	B sounds with tritone
I   Without seconds and sevenths 1. Root and bass are the same Examples: ceg | c it g 2. Root is higher in the chord Examples: c es as | cea | cfa | cf as	II   Without minor seconds and major sevenths . Tritone subordinate a   Only with a minor seventh (without a major second) Root and bass are the same Examples: ceb | cegb b   With a major second and minor seventh 1.   Root and bass are the same Examples: cegbd 1 | c es ga | c es fga | ce as b | ce fis | cde fis | cdeb | cde gis and similar 2.   Root is higher in the chord Examples: c ges b | c es ges as | c es fa | cd f sharp a | cdf as | cd f sharp b | ce f sharp a | cd as b | cd fis | cd as | c es ges b and similar 3.   With several tritoni Examples: ce fis ais | cde g sharp b | cd f sharp g sharp | cde f sharp g sharp a sharp and similar
III    With seconds and sevenths 1.   Root and bass are the same Examples: cdg | cfg | cga | cgb | cgh | cdeg | cefg | cega | ceg as | cd es g | cdfg | c es gb | c es gh | ceghd 1 | c es gbd 1 | cgbf 1 | c es gbd 1 f 1 | cgahd 1 | ce dis 1 | cgd 1 | cgad 1 | cgae 1 | cg as es 1 and similar 2.   Root is higher in the chord Examples: cdf | cda | cdfa | c es b | c des f as | cfab | cdab | cdah | cfd 1 | cf as es 1 | cfae 1 | cfabd 1 and similar	IV    With minor seconds and major sevenths One or more subordinate tritones 1.   Root and bass are the same Examples: cegb des 1 | ceb des 1 | c fis g of 1 | cg as d 1 ce fis gd 1 | c fis g cis 1 d 1 gis 1 and similar 2.   Root is higher in the chord Examples: cf ges a es 1 | cefb des 1 cd f sharp a c sharp 1 e 1 | c des ges af 1 | ceff 1 | ce fis h | ceb es 1 and similar
V    Indeterminate Examples: ce gis | cfb	VI    Indeterminate. Tritone parent Examples: c es ges | c es a | c ges a | c es ges a

Harmony

Chord movements

Hindemith draws on various aspects for assessing and compositionally handling chord movements:

• Superordinate two-part voice: This is formed by the bass voice and the next most important higher voice, which is often, but not always, identical to the upper part. In contrast to the less important filler parts, the requirement to be made of this superordinate two-part voice is that it should form a clean and clearly structured two-part sentence.
• Harmonic gradient: The succession of chords from different groups in the chord table results in a kind of tension curve, which Hindemith calls harmonic gradient , due to the different sound value or degree of dissonance . He uses examples to show how the harmonic gradient can be incorporated into compositional typesetting.
• Root steps : For a quick assessment of chord progressions, "a kind of abbreviated calculation is used that shows the value of a connection and tells us about its direction (about which the gradient does not give any information)." For this, only the root notes of the chords are considered complex progression of the chord masses is reduced to a simple melodic line. Hindemith compares this procedure with the use of logarithms in the numerical realm.
• Leading tones : In the case of connections with tritone chords (because of the inherent tension) the basic offsetting of the basic tones is not sufficient for a reliable assessment and handling. Rather, so-called leadership tones must be used in addition . They are determined from case to case according to slightly varying procedures, the main rule being that that note of the tritone contained in the chord is declared to be the leading note, which forms the best interval with the root note according to the order of precedence of row 2. Hindemith's leading tones are reminiscent of the classic leading tones and, like these, demand a dissolution, although the classical demand for a dissolution by a second step is relaxed.

tonality

• Tonal centers: If several (e.g. three) chords follow one another, their root notes form a broken chord, the root note of which in turn has the tendency to establish itself as the root note (tonic) of the entire group. Hindemith also calls such groups with a definable tonal center tonal circles or districts . For the number of chords required to create a tonal center, Hindemith lays down the rule that if only tritone-free chords are used, three are necessary, while if tritone chords are involved, two are sufficient: the tonic is then the root of the dissolution chord.
• Cadence: A special case is a chord progression called cadence with a strong closing effect. Here the final chord experiences such a strong appreciation through its position alone that it is perceived as a tonic, even if this is not evident from the root constellation alone. Hindemith has no hesitation in recognizing, in addition to cadenting standard movements (such as fourth, fifth, tonic), more unusual keynote sequences as cadence (example: minor sixth, minor second, tonic).
• Graded progression: While very short chord progressions can mainly be covered by the relationships in row 2, the relationships in row 1 come into play for larger harmonic sequences. “The basic tones, which carry the chord loads of larger harmonic relationships, deserve the name steps, their sequence created on the orders of row 1 is called stepped progression. "
• Tonality and modulation : Within a more spacious harmony level, individual tones will gain the upper hand if they are confirmed as central tones by the relationships of row 1. In principle, such a central tone can dominate an entire piece of music and determine its tonality (key). Of course, it can also happen that different passages of a piece are governed by different central tones, so that one can speak of modulation here. The domains of the central tones, i.e. the tonal areas, necessarily overlap, since the step tones are always related to the tonic of the neighboring area (even if more distant).

Difference to traditional harmony theory

What is particularly noticeable as a difference to the traditional view is the elimination of the conventional major / minor tonality, which does not mean that Hindemith no longer differentiates between major and minor triads. What is new, however, is that the key of pieces of music is no longer based on major or minor scales, but rather on the chromatic scale, the tones of which cluster around a tonal center in the sense of the relationships given by row 1. The key bindings that are detached from major and minor can aptly be described as free tonality . In terms of harmony, there are no limits to this free tonality: every chord can be accommodated in it without any problems. Another advance of Hindemith's harmony is the clear classification of the chords, which makes the altered and lead chords used for this purpose in traditional harmony superfluous.

Atonality, polytonality

One cannot escape the tonal affinities established in nature, says Hindemith, and that is why it is “completely impossible to invent tone groups without tonal relation. The tonality is a force like the gravitational pull of the earth. ”Correspondingly, strictly speaking,“ atonal ”music could not even exist, unless it was understood to mean only harmonic disorder. He criticizes the twelve-tone technique of the Vienna School as an arbitrary, even unnatural artifact. He mockingly points out that the same composers who pay homage to harmonic freedom "have succumbed to a formalism in architectural questions that makes the artistry of the early Dutch counterpoints seem like child's play." Hindemith also leaves the so-called polytonality as an entertaining gimmick apply to the composer, but rejects it as a working principle of a harmonic setting method, since the listener cannot follow the tonalities running alongside one another separately, but can only perceive them as the resulting overall tonality.

Melody

With the attempt to teach melody, Hindemith is breaking new ground, because the previous teaching systems did not address it. Hindemith, too, immediately limits his efforts to the effect that he intends to disregard the rhythm, although it should not be missing in a complete teaching of melody, and to postpone its inclusion to a later point in time.

• Harmonious bond, melody levels: Hindemith first deals with the inherent harmonic aspects of the melody. He points out that broken chords always appear in melodic lines, either in immediate succession or interrupted by passage or secondary notes. The fundamental tones of such harmoniously linked sections - which often cannot be sharply delimited and can overlap - result in a melody level , for which, in a weakened form, similar criteria apply as for the above-mentioned harmony level .

• Seconds: The seconds are extremely important for the construction of melodies. On the one hand, they perform detailed work in a confined space, for example to bridge the larger, harmoniously stronger intervals, and Hindemith devotes an entire chapter to the study of case studies. On the other hand, seconds can become signposts for the large-scale melody and then acquire a dominant position. Hindemith coined the term second for this phenomenon . A melody can have several, often intertwined, seconds. They are determined by connecting the high and low points that are every second.

Hindemith is of the opinion that a melody is particularly convincing if it is possible to create the melody level and second rate “in a beautiful balance”.

Analyzes

In the final chapter of his work, Hindemith tries to prove the universal applicability of his system to all types of music. To this end, he analyzes the following very different music examples in detail:

1. Dies irae ( Gregorian chant )
2. Guillaume de Machaut : Ballad Il m'est avis
3. Joh. Seb. Bach : Three-part Invention in F minor
4. Richard Wagner : Tristan and Isolde , prelude
5. Igor Stravinsky : Piano Sonata 1924, 1st movement
6. Arnold Schönberg : Piano piece op.33a
7. Paul Hindemith : Mathis the painter , prelude

With the exception of the Gregorian chant, which only allows a melodic analysis, he carries out a melodic and harmonic analysis of all pieces with varying degrees of detail, whereby in addition to melody levels or seconds and harmonic gradients, he attaches particular importance to working out the harmony levels and the tonal areas seems to lay.

That he such tonal districts even in a specifically twelve-tone - atonal attempts to detect conceived work like the Schoenberg Piano Pieces, suggests that he apparently wanted to teach the atonal direction he refused vehemently, a lesson. By transferring a twelve-tone piece to the unintentionally inherent tonality, he hits the idea of ​​atonality a violent blow.

The exercise books

In contradiction to the title, the theoretical part does not contain any practical instruction or guidance on composition, but at most provides the composer with analytical tools with which he can control and improve his work. In contrast, the exercise books aim to provide the composition student with practical exercises, rules and tasks. The exercise book for the two-part movement, published in 1939, consists of eleven exercises, in the course of which a total of 65 rules are established, some of which, however, only function as ad hoc rules and are canceled as the exercise progresses. The 56 tasks are intended to enable the student to understand two-part polyphonic sentences of all styles and to compose them himself. The extension for the three-part movement did not appear until posthumously in 1970.

Remarks

1. ↑ Hindemith likes to use the comparison with the craft of the carpenter. Just as he has to carefully observe its properties when gluing the wood together, the composer must also know and take into account the natural properties of the clay material.
2. ↑ Of course you could also choose any other tone as a starting point.
3. ↑ The number of overtones (partials) includes the fundamental as number 1.
4. ↑ In Euler's Tonnetz , the chromatic scale is written as C 'Db' Eb, EF, F sharp / 'Ges G' Ab, AB, HC

Individual evidence

1. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, pp. 45, 46.
2. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 51.
3. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 50.
4. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 57.
5. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 67.
6. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 113.
7. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 150.
8. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 173.
9. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 183.
10. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 186.
11. ↑ Paul Hindemith: Instruction in clay composition (theoretical part) . Schott, Mainz 1937, p. 233.

See also

• Ludus tonalis
• Free tonality