wave
A wave is a spatially propagating periodic ( oscillation ) or one-time ( disturbance ) change in the state of equilibrium of a system with regard to at least one location- and time-dependent physical variable. A distinction is made between mechanical waves that are always bound to a medium and waves that can also propagate in a vacuum (e.g. electromagnetic waves , matter waves or gravitational waves ). In media, the propagation of a local disturbance is conveyed through the coupling of neighboring oscillators (physical quantities that can oscillate). A wave transports energy , but not matter . H. the neighboring oscillators transport the disturbance through space without moving themselves on average over time. Directly perceptible waves are, for example, sound waves , water waves and light .
Wave types
Waves are divided into several categories: the "classic" longitudinal and transverse waves (of which mixed forms such as torsion waves can also occur) as well as matter waves (according to Louis de Broglie's theory , a moving particle also has a wavelength that can also be demonstrated with the appropriate experimental setup can be) and probability waves , which describe the states of physical systems in the context of quantum physics . Gravitational waves compress and stretch space-time transversely to their direction of propagation; the superposition principle does not apply to them.
Mechanical longitudinal waves can propagate in any medium, whether solid , liquid or gaseous , whereas mechanical, pure transverse waves can only propagate in solid bodies. Electromagnetic waves in lossless media (e.g. in a vacuum) are transversal.
Longitudinal wave
Waves that oscillate parallel to the direction of propagation are known as longitudinal or longitudinal waves. An important example is sound, which in gases and liquids always propagates as a longitudinal wave.
Mechanical longitudinal waves are pressure waves . This means that in a medium, zones with overpressure or compressive stress (or negative pressure or tensile stress) propagate or shift or spread in the direction of propagation. The individual particles in the propagation medium, atoms or molecules , swing back and forth in the direction of propagation by the amount of the amplitude. After passing through the oscillation, the particles move back to their rest position, the equilibrium position.
The power of a longitudinal wave is proportional to the square of the amplitude or the compressive stress, see also sound pressure and sound velocity . Longitudinal waves have a higher speed in the same solid medium than transverse waves of the same type with otherwise the same parameters.
Transverse wave
Waves that oscillate perpendicular to the direction of propagation are known as transverse, transverse, shear or shear waves. Only transverse waves can be polarized .
Examples are electromagnetic waves, gravitational waves, bending waves and plasma waves .
Sound waves in solids and seismic waves can also propagate as transverse waves if the material is suitable.
As surface waves, water waves are usually a mixture of longitudinal and transverse waves, but can also occur as a standing wave ( seiche ) as a pure transverse wave . They form either gravitational or capillary or a transitional form between the two.
Mathematical description
| designation | symbol | Relationships | ||||
|---|---|---|---|---|---|---|
| amplitude |
|
|||||
| Wave vector | Direction of propagation | |||||
| Circular wavenumber | ||||||
| wavelength | ||||||
| Angular frequency | Dispersion relation | |||||
| frequency | ||||||
| Phase velocity | ||||||
| Group speed | ||||||
| phase |
Several quantities are necessary for the mathematical description of waves. These include amplitude, phase and propagation or phase velocity. The adjacent table provides an overview of the sizes that are necessary for a complete description.
Wave function
Mathematically, one speaks of a wave when the wave function , i.e. the equation that mathematically describes the wave , is a solution to a wave equation . These functions generally depend on location and time .
The deflection at the location indicates the time . Functions of this type correspond to the idea that waves are spatially extended vibrations. It is not easy to specify a general function for every type of shaft. Very simple solutions of the wave equation are therefore often used and the real wave is viewed as a superposition of many of these solutions. The most common elementary solutions are the plane wave and the spherical wave .
amplitude
The amplitude is the maximum possible deflection of the shaft. In the case of waves - in contrast to vibrations - it is a vector quantity, since in addition to the strength of the deflection, its direction is also decisive. If the direction of propagation is parallel to the amplitude, it is a longitudinal wave, if it is perpendicular, it is a transverse wave. In both cases the intensity of the wave is proportional to the square of the amplitude.
phase
The phase of a wave indicates in which section within a period the wave is at a reference point in time and location. So it determines how big the deflection is. In the example of a plane wave is the phase at the time at the location . The phase therefore depends on the two parameters wave vector and angular frequency .
Examples
The mathematical formulation for a harmonic (also: homogeneous, monochromatic) plane wave in three-dimensional space is in complex notation :
A spherical wave can be described with the following equation:
Generation of waves
Sources for waves can be pulse-shaped excitations, vibrations or periodic oscillations. Periodic mechanical and electromagnetic waves can be generated by periodic vibrations. A simple example is a swinging pendulum: On such a pendulum there is, for example, a pen under which a sheet of paper is pulled at a constant speed. The pen attached to the pendulum now describes a sinusoidal wave on the strip of paper, which is the medium of propagation. In this example, the wavelength depends on the speed at which the paper strip is moved. The amplitude of the wave is determined by the maximum swing of the pendulum.
An electromagnetic wave can be generated by an antenna that is connected to an electric vibration generator. A so-called oscillating circuit can be used as the oscillation generator , in which the electric current flows back and forth between a coil and a capacitor. The total electromagnetic energy is periodically converted in the resonant circuit from electrical energy (mediated by the electric field in the capacitor) into magnetic energy (mediated by the magnetic field of the coil). If this happens at a suitable frequency for the antenna used, part of the energy is efficiently radiated from the antenna into the room in the form of an electromagnetic wave. This effect is of particular importance in wireless communication.
Superposition of waves
Waves occurring in nature are rarely pure monochromatic waves, but rather a superposition of many waves of different wavelengths. The superposition is done by the superposition principle , which mathematically means that all wave functions of the individual waves are added. The proportions of the wavelengths are called the spectrum . Examples:
- Sunlight is a superposition of electromagnetic waves. The spectrum covers a wavelength range from infrared to visible light to ultraviolet . Such spectra are also called continuous .
- A musical tone of an instrument is composed of a fundamental tone and several harmonics . The different proportions of harmonics are the reason why a trombone sounds different than a flute. Such a spectrum is called discrete because it is composed only of individual, clearly separated wavelengths.
Various effects can occur:
- Interference - If waves are superimposed, this can lead to a structural reinforcement , but also to a partial or even total cancellation of the wave (if both wavelengths and frequencies are the same and the waves oscillate exactly in opposite directions). This phenomenon plays a role in everyday life, for example in the case of unwanted multi-path reception - waves from a transmitter arrive at one location on different paths and can sometimes cancel one another there.
- Standing wave - When two opposing waves of the same frequency and amplitude are superimposed , standing waves are formed. These do not spread, but form spatially constant oscillation patterns: At the so-called movement arteries they oscillate with doubled amplitude and the original frequency, at the movement nodes in between the amplitude is zero at all times. This phenomenon is a special case of interference. It occurs in particular in front of a reflective wall or between two suitably matched walls which together form a resonator .
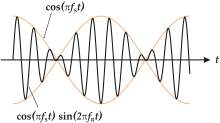
- Beat - A superposition of two waves of neighboring frequencies leads to a beat. The amplitude of such a wave increases and decreases periodically - the closer the frequencies are to each other, the slower this process occurs (in time). This effect is used, for example, when tuning musical instruments - the beat frequency is adjusted too close to zero. The beats of the Leslie loudspeaker are also typical . People find its slow beats pleasant.
- Wave packet - The superposition of waves with all frequencies from a frequency band creates a wave packet. Here the envelope of the wave shows only a single mountain, in front of and behind this the amplitude is negligible. Since the phase velocity of a wave in waveguides and dispersive media is frequency-dependent, wave packets dissolve with increasing time. When transmitting messages using waves, the resulting broadening of wave packets must be taken into account.
literature
- Gavin Pretor-Pinney: A little wave science for amateurs. ( The Wavewatcher's Companion. 2010), Berlin 2011, ISBN 978-3-8077-1075-4 .
- Eduard Rhein : Miracle of the waves: Rundfunk u. Television, shown f. jedermann , issue 69. – 80. Th., German publ. D. Ullstein AG, Berlin-Tempelhof 1954. DNB