overtone
Harmonics (even partial or partials, rare Aliquottöne, overtones or Beitöne ) are the mitklingenden addition to the fundamental components of almost any instrumental or vocal generated musical tone . In the acoustic sense, this is almost always not a tone ( sine tone ), but a sound or mixture of tones , i.e. a sound event that is primarily composed of several sinusoidal partials . The lowest partial is called the fundamental and in most cases determines the perceived pitch , while the other partials, the overtones, influence the timbre .
With many musical instruments, especially with aerophones such as the flute and chordophones such as the violin or the guitar , the frequencies of the overtones are approximately whole-number multiples of the fundamental frequency. This means that overtones with frequencies of around 880 Hz or around 4400 Hz can be added to a fundamental tone with a frequency of 440 Hz , but not, for example, of 550 Hz.Tones of this kind, whose frequencies are integral multiples of the fundamental frequency, are also known as harmonics .
With other sound sources (e.g. tubes, rods, plates or bells ), vibrations also occur whose frequencies do not have an integer relationship to the perceived fundamental frequency, which can make it difficult to recognize a certain pitch or the tone as unclean or in extreme cases is perceived as jarring. Such partials are also called inharmonics.
While partials are components of an overall sound that is created by stimulating all or more of the possible natural vibrations of an oscillating body, with the conceptually related natural tones of wind instruments, individual harmonics are stimulated by so-called overblowing , which are then perceived as sounding tones. The actual keynote is thus suppressed. The same applies to the harmonics of stringed instruments .
Depending on the sound source, the composition of the sound spectrum is very specific, so that in addition to noise components and factors in the course of the signal over time, the overtone content in particular is responsible for the characteristic timbre of musical instruments as well as human and animal voices. Frequency ranges typical for voices and instruments, in which the overtones are particularly amplified by resonance and are therefore primarily decisive for the timbre, are called formants .
Harmonics
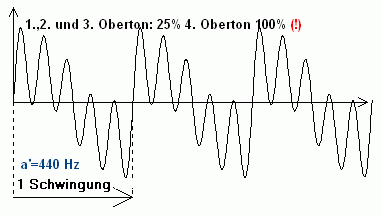
As harmonic partials is called a harmonic sound, ie its fundamental tone and the overtones whose frequencies are integer multiples of the frequency of the fundamental. In the following figure, the large sine wave on the left represents the fundamental; In the picture to the right, harmonic overtones in the form of narrower sine waves are superimposed on the large wave.

|
|
Audio sample: Building a harmonic sound from sine tones
In the adjacent audio example, a harmonic sound is successively built up from its electronically generated sinusoidal partials. The more overtones are added, the more the suggested residual tones add up to the actual fundamental. This effect is z. B. used in organ building with so-called acoustic registers that sound deeper than they actually vibrate.
Harmonic oscillations are always related to the fundamental frequency . How exactly this relationship is described depends on the chosen mathematical model. The choice of the fundamental frequency is objectively difficult and, in relation to music, is primarily determined by the perceived or notated fundamental tone. When analyzing or synthesizing sound events, the basic frequency can also be chosen differently from an acoustic or metrological point of view. The fundamental and overtones must therefore always be understood in context.
In many cases, however, a simple description model is sufficient that assumes the frequencies of the harmonics as integer multiples of a fundamental frequency perceived as a sound.
Explanatory example: Concert pitch a 1 and the first five harmonics
This table shows the concert pitch a 1 as the fundamental and its first four overtones with their respective order n and their frequencies. The nth harmonic generally has the frequency n · f.
| frequency | 1 x f = 440 Hz | 2 · f = 880 Hz | 3 * f = 1320 Hz | 4 x f = 1760 Hz | 5 · f = 2200 Hz |
|---|---|---|---|---|---|
| Note designation | a 1 | a 2 | e 3 | a 3 | c sharp 4 |
| order | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 |
| Base frequency | 1st overtone | 2nd overtone | 3rd overtone | 4th overtone | |
| 1st partial | 2nd partial | 3rd partial | 4th partial | 5th partial | |
| 1st harmonic | 2nd harmonic | 3rd harmonic | 4th harmonic | 5th harmonic |
The fundamental is the 1st harmonic, an octave above is the 2nd harmonic, which is the 1st overtone.
The simple harmonic model - overtone series

Knowledge about overtones has been gained from the example of vibrating strings since ancient times . It is assumed that a string shortened by half produces a tone with twice the number of vibrations, a string reduced to a third produces three times the number of vibrations, etc. For musical practice, e.g. overblowing wind instruments, playing flageolet tones on stringed instruments, the Overtone singing or organ registration , this simple model is usually sufficient. When applied to other sound sources such as B. strongly tensioned piano strings, however, this model reaches its limits.
The figure on the right shows (arbitrarily limited to the first seven) the natural vibrations of a string. Under certain conditions, the string can execute each of these natural vibrations separately ( flageolet tones ), but usually all or at least several of these natural vibrations are excited at the same time, so that the resulting oscillation consists of a complex superposition of these partial oscillations.
The human ear perceives periodic vibrations as tones (in the sense of musical tones), with the period of vibration determining the perceived pitch . If one analyzes the amplitude spectrum of an audio signal of an approximately periodic oscillation z. B. with the help of the short-term Fourier transform , this consists of
- a keynote corresponding to the period of oscillation
- and the harmonic overtones with frequencies that are integer multiples of the fundamental frequency.
If you list the partials in terms of increasing frequency, you get the partial or overtone series:
The overtone series
In the following, the first sixteen partials related to the root C are shown as an example. This restriction has been chosen arbitrarily for reasons of clarity. Theoretically, the series of partial tones continues upwards with ever decreasing intervals to infinity.
As a note example
If the partial tones are represented by notes, it must be taken into account that, due to the continuously decreasing tone spacing, an exact reproduction in musical notation (at least in the higher range of the partial tone series) is only approximately (and ultimately no longer) possible. Also, not all overtones match the pitches of the common tuning systems . In the following note example, the overtones are compared with the tones of the equal pitch . The deviations up or down are given in cents .
While in the case of equal tuning, apart from the fundamental and its octaves, no tone exactly matches the partial tone series, the deviations are significantly less common in pure tuning .
As a table
The colors used in the table are based on music-color synesthesia .
| Root note - overtone no .: | Keynote | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | 9 | 10 | 11 | 12 | 13 | 14th | 15th |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Partial no: | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | 9 | 10 | 11 | 12 | 13 | 14th | 15th | 16 |
| Multiples of the basic frequency: | simple | double | triple | fourfold | fivefold | sixf. | sevenf. | eightf. | ninef. | tenfold | eleven times | twelve times | thirteenf. | fourteenf. | fifteenf. | sixteenf. |
| Example f in Hz: | 66 | 132 | 198 | 264 | 330 | 396 | 462 | 528 | 594 | 660 | 726 | 792 | 858 | 924 | 990 | 1056 |
| Grade: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Note name: | C. | c | G | c 1 | e 1 | g 1 | ≈ b 1 | c 2 | d 2 | e 2 | ≈ f 2 | g 2 | ≈ as 2 | ≈ b 2 | h 2 | c 3 |
| Relation to the tone below: | 1: 1 | 2: 1 | 3: 2 | 4: 3 | 5: 4 | 6: 5 | 7: 6 | 8: 7 | 9: 8 | 10: 9 | 11:10 | 12:11 | 13:12 | 14:13 | 15:14 | 16:15 |
| Interval to the tone below: | Prime | octave | perfect fifth | pure fourth | major third | minor third | - | - | large whole tone | small whole tone | - | - | - | - | - | diatonic semitone |
Table footnotes
- ↑ A minor third (frequency ratio 6 ⁄ 5 ) above the concert pitch a ′ with 440 Hz is the tone c 2 with 528 Hz. The three octaves lower C has a frequency of 66 Hz.
- ↑ 7th overtone = 462 Hz ( natural seventh ). Deviation from b 1 = 475.2 Hz of the pure tuning ≈ 49 cents. Note: The unit of cents is used primarily for the representation of the subtle differences in size of the intervals , where an equal semitone corresponds to 100 cents and an octave corresponds to 1200 cents. The calculation is made using the logarithm of the frequency ratio to base 2. Here 1200 log 2 (475.2 / 462) ≈ 49 cents.
- ↑ 11th overtone = 726 Hz ( Alphorn-Fa ). Deviation from f 2 = 704 Hz or f sharp 2 = 742.5 Hz of the pure tuning ≈ 53 cents or 39 cents.
- ↑ 13th overtone = 858 Hz. Deviation from a flat 2 = 844.8 Hz of the pure tuning ≈ 27 cents.
- ↑ 14th overtone = 924 Hz ( natural seventh ). Deviation from b 2 = 950.4 Hz of the pure tuning ≈ 49 cents.
- ↑ The musical interval of an octave corresponds to a doubling of the frequency.
The last line of the table shows that all intervals of the diatonic scale (see pure tuning ) can be derived from the overtone series. In particular: semitone (frequency ratio 16 ⁄ 15 ), major and minor whole tone ( 9 ⁄ 8 and 10 ⁄ 9 ), minor third ( 6 ⁄ 5 ), major third ( 5 ⁄ 4 ), fourth ( 4 ⁄ 3 ), fifth ( 3 ⁄ 2 ) and octave ( 2 ⁄ 1 ).
Limits of the simple model
With many musical instruments or with vowels of the human voice , a significant part of the sound consists of periodic vibrations, which can be described in good approximation with the simplified model conception of the fundamental tone and harmonic overtones, for example with vibrating strings of stringed instruments ( chordophones ) or vibrating air columns of Wind instruments ( aerophones ). However, in reality there are more or less strong deviations from the theoretical integers of the overtones.
Inharmonicity
Deviations from the harmonic relationships of the partials are individually dependent on the type of instrument. These deviations, known under the term inharmonicity, are mainly triggered by the bending moment of the string , for example in the piano . Because of the high string tension, very thick strings are required, at least for the bass strings, which increases this effect. In addition, higher harmonics are more affected than lower ones. The more precise analysis of such harmonics is much more complex and therefore requires more complex models for the description than the analysis and description of very harmonic tones. (See also audio signal ).
Noise components
In addition, there are also non-periodic oscillations that have a rather broadband frequency spectrum and cannot be described by fundamental and harmonic overtones, e.g. B. Stroke noises in string instruments , blowing noises in wind instruments and organ pipes, and consonants in the human voice . The analysis of these sound components requires modern electronic measurement technology and mathematical models, the solutions of which can only be calculated with powerful computers.
Blur
In mathematical terms, vibrations are only sinusoidal if they have both lasted infinitely long and will continue to last infinitely long. In practice, vibrations are only quasi-periodic or almost periodic. The sine function extends into infinity on both sides and cutting off the duration mathematically leads to something else, a time-limited wave. As a psychoacoustic consequence, when cutting off long-lasting, continuous, static sine tones or mixed sine tones, broadband artifacts result.
With short-term processes of this kind - as they occur with all instruments where energy is not always supplied, especially with plucked and percussion instruments (including the piano) - the basic requirement of the continuous tone is not even approximately fulfilled.
In the engineering culture, it was mostly assumed that processes are long-lasting and slowly changing (this is the case with the modulation of a radio station). Only then do the Fourier transform and the terms implicitly following it in the article make sense. Not until the turn of the 21st century. the insight has gained acceptance that the wavelet transformation must be used for processes that change quickly and last for a short time , whereupon terms such as "frequency" have to be reinterpreted. Since then, a variety of different methods have been used for root key recognition.
Music essentially involves such processes. In this respect, criticism of traditional ideas must also be exercised from this point of view. Our ideas are too much shaped by the models that are completely sufficient for electronics in many areas today. An excerpt from Zamminer's Die Musik und shows that people were already aware of the complex relationships before Hermann von Helmholtz published a mathematical theory to explain timbre through overtones in The Doctrine of Tone Sensations as the Physiological Basis for the Theory of Music (1863) The musical instruments of 1885: “All sounding bodies, whatever their substance, their shape, their state of elasticity and tension, are capable of an infinite number of types of division and just as many overtones in addition to the vibrations in their entirety, which give the fundamental tone. The vibrational states which they are able to assume are all the more varied the less simple their form is. Only cylindrical and prismatic columns of air, and similarly vibrating rods of small diameter, have such a simple harmonic upper row as the tensioned strings; The number of overtones is already far richer in bodies which, like plates and taut skins, spread out in flat or curved surfaces, the most varied of those of solid masses and air spaces that are arbitrarily extended in every sense. "
Overtones and timbre
Overtones of the human voice
In the human voice , just like in most sound-producing physical systems, a complex overtone spectrum resonates. In the special vocal technique of overtone singing , these high frequencies can be made to dominate.
The different sound of vowels comes about through their specific overtone structure. Due to the individual size and shape of the mouth and throat, some frequencies are amplified by resonance , others are attenuated. The frequency ranges that are amplified are also called formants .
Harmonics of different instruments
The specific sound of an instrument results from the answers to the following questions:
- Which overtones are there anyway?
- How loud are these overtones in relation to each other?
- How do the volume and frequency of the individual overtones change while the tone is being played?
- Which additional noises (impact noises, blowing noises ...) are added?
The following instruments have a particularly characteristic partial tone structure:
- String instruments have a very rich partial range.
- Clarinets emphasize the volume of the odd partials.
- In the bassoon , the fundamental is much weaker than the first overtones.
- Bells often emphasize the thirds very strongly and the overtone composition is complex.
- Tuning forks almost only produce the keynote.
In instruments with simple overtone compositions, the frequencies of the overtones are approximately whole-number multiples of the frequency of the fundamental. These include the chordophones (string instruments) and the aerophones with a vibrating column of air. Of course, this is only an idealized assumption; so there is an inharmonicity with real (not infinitely thin) strings. The very small deviations from the ideal harmonics make the sound of an individual instrument distinctive and lively.
For most woodwind instruments this is very close to the idealized assumption, and for many string instruments this is also quite true. In the case of the piano, however, the integral frequency ratio is only approximately fulfilled. The very high overtones in particular are quite far from the frequencies with integer ratios to the fundamental. The higher you climb the ladder of the overtones, the more their frequencies deviate from the precisely harmonic ones. It has even been found that the timbre of the piano is very much related to this deviation from the precise harmonic overtones. For example, imitations of a piano do not sound particularly piano-like if this deviation in the overtone series is not taken into account in the artificial generation of the tone.
The natural frequencies and their harmonic overtones depend on the respective sound generator and are determined by the dimensions and nature of the body. There are instruments in which the overtone compositions can be described relatively easily, and others which require very complex description models. In instruments with complex overtone compositions, there are many frequencies of the overtones in complex non-integer relationships to one another. The overtones of the membranophone with a round membrane have the natural frequencies of a Bessel differential equation . With idiophones , depending on the shape of the body of sound, very different series of overtones can result - with stick playing, for example, it is the natural frequencies of the bending vibration of a beam .
Overtone spectra artificially produced from sine tones are called synthetic sounds (see sound synthesis , synthesizer ). A pure sawtooth oscillation is characterized by the fact that it contains all of its overtones as its fundamental, which is why it was preferred to use it as the output oscillation in the days of analog-electronic musical instruments.
Effect of overtones: brilliance and dullness
The proportion of overtones in the overall spectrum and the resulting timbre can be determined by words such as brilliance, sharpness, purity, dullness and the like. a. to be discribed.
In general, tones sound more brilliant (violin), sharper (trumpet) or more colorful (oboe, bassoon), the more overtones they have, and the purer and clearer (flute) or paler or duller (deep clarinet, covered organ registers ), depending less they have.
Pure tones without overtones, i.e. sine tones , can practically not be generated at all. As an approximation, they can only be generated mechanically with very low sound levels (tuning fork or cavity resonators, very gently excited). The generation of approximately pure sine tones is possible electronically without any problems. At lower frequencies they sound dull, wide and flowing, certain organ registers come close to that. At higher frequencies the difference to sounds with overtones becomes smaller because these overtones are outside the audible range. An example of the situation for medium frequencies is the 1000 hertz tone of the television test pattern, but the loudspeaker already adds its own overtone spectrum due to its distortion. Since all the energy only occurs in a narrow frequency range, high-level sine tones can be very unpleasant. In general, sine tones are a touchstone for every loudspeaker, as the risk of electrical and mechanical overload is very high on the one hand, and on the other hand distortion products with audible levels are immediately noticeable and mechanical design problems with occasional rasping or hissing resonances are revealed.
In a multi-way loudspeaker ( electro-acoustics ), the tweeter is primarily responsible for the brilliance, i.e. for the sound brightness and the timbre of the reproduction.
With mechanical musical instruments, higher overtones are usually quieter ( lower level ) than lower ones :
- On the one hand, with mechanical tone generators, higher frequencies are only stimulated much weaker than lower ones (e.g. the oscillation amplitude of the overtones decreases with increasing frequency in a vibrating string).
- On the other hand, higher frequencies in the air are more attenuated. For this reason, the brilliance of the reproduction is usually relatively poor when sounding over large areas.
Audibility of overtones
As a rule, overtones are not perceived individually, but result in the sound of a tone . In certain cases or under special conditions, however, they can also be heard or made audible individually.
- Some people are able to selectively hear single overtones from a sound without any help. This is especially true for very stable tones such as long sustained tones from organ pipes .
- The singing technique of overtone singing makes the overtones clearly perceptible. Examples are the overtone singing of Mongolian and Tuvinian peoples. In western music, too, there has been a revival of overtone culture since the late 1960s.
- Overtones can also be clearly heard in the instrumental area. Typical instruments for this are e.g. B. the didgeridoo , the fujara or singing bowls .
- With string instruments, tones at the pitch of overtones can be generated by playing the flageolet (see flageolet tone ). The gripping hand only touches the string lightly instead of pressing it onto the fingerboard. However, a different tone then usually sounds than with normal grasping.
- There are three ways to make overtones audible on the piano :
- By gently pressing down the keys of a chord from the overtone series without the hammers touching the string , and then striking the root note in the bass range briefly and strongly. The overtones now create a resonance on the undamped strings of the keys that are held down, which can be clearly heard.
- By silently pressing a key in the bass range in the manner described and then striking one or more notes from the associated overtone series briefly and forcefully. The undamped bass string is stimulated by resonance to vibrate with the frequencies of these overtones. The struck notes continue to sound like an echo, although the associated strings have been muted.
- You can also create a flageolet tone on the piano. To do this, lightly press the required point on a string and hit the corresponding key with the other hand. The same works by preparing the string, the best material for this is rubber.
- The first effect in particular is also used by composers in their works (e.g. Béla Bartók : Mikrokosmos, Volume IV).
Applications
The organ and its registers
The harmonic series of overtones on the organ is particularly important . With different organ registers , each of which with a few exceptions produce harmonic overtones ( aliquots ), timbres can be created through a simple type of additive synthesis . With pipe organs only an "on" or "off" the register is possible. The most commonly used harmonic overtones are octaves (2nd, 4th, 8th, 16th, ... partial), fifths (3rd, 6th, 12th, ... partial) and major thirds (5th, 10th, ... partial), in modern organs also the minor seventh (7th, 14th, ... partial) and the major ninth (9th, 18th, ... partial).
A sound synthesis inspired by this takes place at the Hammond organ . The proportions of the partials can also be varied using sliders .
Residual tones
The human auditory center is able to perceive the fundamental frequency for a (even partial) sounding overtone spectrum, even if it is not sounding. This "added" keynote is also called the residual tone .
Music theory and didactics
The existence of overtones has been used for a long time to scientifically explain and justify the tonal systems of music, usually based on the simple model of integer frequency or string length ratios.
- The first theory related to overtones is attributed to Pythagoras , this was around 2500 years ago.
- For didactic purposes (teaching the accompaniment, figured bass, harmony and melody as well as composition theory) Johann Bernhard Logier (1777–1846) was probably the first to use the overtone series. His doctrine of the "harmonious sounding" tones was always controversial during his lifetime; His didactically highly reflective works with their simple, basic rules that build on each other can, however, be regarded as the beginning of modern music theory that is still valid today.
- One of the last attempts to justify a theoretical system of the overtone series and other acoustic phenomena (eg. As combination tones ) can be found in Paul Hindemith in his instruction in music theory . Hindemith's system is also very controversial in the professional world. Even today, real tones or sounds can only be grasped mathematically to a limited extent, which is why every system reaches its limits at some point. An aesthetic system is therefore difficult to legitimize scientifically.
Undertone series
If you mirror the harmonic overtone series, the result is the theoretical harmonic undertone series which is symmetrical to it and which is created by frequency division, supplemented downwards. Undertones are extremely rare in nature; they sometimes occur with bells and gongs. It is not certain whether these are actually notes from a series of undertones. In practice, they are produced in trautonium , subharchord and undertone singing.
Hugo Riemann in particular often used the term undertone series in his textbooks and musicological treatises, and interpreted it in the "two-root theory" (major / minor dualism) as the basis of his functional theory.
Remarks
- ↑ Pure sine tones can only be generated with electronic means. With tuning forks or flutes, however, sound events can be produced that come very close to sine tones.
- ↑ a b With the terms "partial" and "partial" the basic frequency is counted. If one speaks of "overtone", the basic frequency is not counted. The ordinal number of an overtone is therefore always one less than the ordinal number of a partial tone.
See also
- Natural tone series
- Vowel triangle , vocal trapezoid , flageolet tone , overtone singing
- Psychoacoustics , difference tone
- Mood (music)
- Fourier analysis , oscillation , square wave , tilting wave
- List of audio terms
literature
- Hermann von Helmholtz : The theory of tone sensations as a physiological basis for the theory of music. Vieweg, Braunschweig 1863, ( online ).
- Keyword overtones. In: Johannes Kunsemüller (Hrsg.): Meyers Lexikon der Technik and exact natural sciences . Bibliographisches Institut AG, Mannheim 1970, p. 1844 .
- Keyword partials. In: Willibald Gurlitt , Hans Heinrich Eggebrecht (Hrsg.): Riemann Music Lexicon (subject part) . B. Schott's Sons, Mainz 1967, p. 942 f .
- Keyword overtones. In: Marc Honegger, Günther Massenkeil (ed.): The great lexicon of music. Volume 6: Nabakov - Rampal. Updated special edition. Herder, Freiburg im Breisgau a. a. 1987, ISBN 3-451-20948-9 , p. 82 ff.
- John R. Pierce: Sound. Music with the ears of physics. Spectrum, Heidelberg / Berlin / Oxford 1999, ISBN 3-8274-0544-0 .
Web links
- The partial vibrations of a drum in animated graphics
- Harmonics, partials, partials and overtones (PDF file; 255 kB)
- Partial density and partial series (PDF file; 47 kB)
- Differentiate overtones from harmonics, partials and partials (PDF file; 42 kB)
- The frequency ratios that result for intervals from the overtone series
- Audio samples of the sung overtone series or natural tone series
- Overtone spectra of various instruments
- The overtone series in the human voice
- Overtone singing
- Overtones, harmonics and partials from the fundamental frequency
- Partials and sound
- The small overtone course (PDF file; 1.5 MB)
- How the overtones arise
Individual evidence
- ^ Entry in Meyer's Large Conversation Lexicon from 1905.
- ↑ a b Practical Applied Mathematics: Modeling, Analysis, Approximation, Sam Howison, 2005, ISBN 0-521-60369-2 , Chapter 15.3, page 209 ff.
- ↑ Signals, Systems and Sound Synthesis: Basics of Computer Music. Volume 2 of Zurich Music Studies. Martin Neukom, 2005, ISBN 3-03910-819-0 , page 56, online.
- ↑ Signals - Processes - Systems: A multimedia and interactive introduction to signal processing. Ulrich Karrenberg, 2009, ISBN 3-642-01863-7 , page 84, online.
- ↑ Johann-Markus Batke: Investigation of melody search systems as well as processes for their functional testing. 2006, ISBN 3-86727-085-6 , page 71, online.
- ^ Friedrich Georg Karl Zamminer: The music and the musical instruments in their relation to the laws of acoustics. 1855, page 176, online.
- ↑ See above all: JB Logier: System of music science and practical composition with the epitome of what is usually understood by the term general bass. Berlin 1827, p. 11: Circle of fifths, p. 15 ff. Figured bass, from p. 53 the teaching of overtones begins.

